显著性检验
游戏引擎
pygame
进程
雨滴传感器
flink watermark
便签
前后端分离考试系统
进程替换
DASCTF2022十月挑战赛
图相似度预测
ROBOGUIDE
ReentrantLock
condition
高校失物招领系统
期末考试
httpClient
数据库增删改查
pytorch配置GPU版本
memory
概率论
2024/4/11 15:24:12概率统计Python计算:贝叶斯公式
根据完备事件组A1,A2,…,AnA_1, A_2,\dots , A_nA1,A2,…,An的先验概率序列P(A1),P(A2),…,P(An)P(A_1), P(A_2), \dots, P(A_n)P(A1),P(A2),…,P(An),对事件BBB的似然度序列P(B∣A1),P(B∣A2),…,P(B∣An)P(B|A_1)&a…
概率统计Python计算:连续型随机变量分布(norm)
scipy.stats的norm对象表示正态分布,下表说明norm的几个常用函数。
函数名参数功能rvs(loc, scale, size)loc,scale:分布参数μ\muμ和σ\sigmaσ,缺省值分别为0和1,size:产生的随机数个数,缺省…
概率统计Python计算:随机变量的分布函数
任何随机变量XXX都有其分布函数(或称为累积分布函数) F(x)P(X≤x),x∈(−∞,∞).F(x)P(X\leq x), x\in (-\infty,\infty).F(x)P(X≤x),x∈(−∞,∞). 例1 向半径为rrr的圆内任一投掷一个点,求此点到圆心的距离XXX的分布函数,并计算…
概率论与数理统计之贝叶斯公式
若为试验E的一个完备事件组,B为E的任一事件,且,则:。这个公式也被称为贝叶斯公式。 根据乘法公式有:根据全概率公式有:其中称为先验概率,称为后验概率例题:设一地区居民的某种疾病的…
5003笔记 Statistic Chapter6-Cross validation and bootstrapping
训练误差和测试误差不是一个重要程度,训练误差可以低于测试误差。测试误差小,说明模型泛化性能好。 当test error开始上升时,模型就是过拟合了。Train和Test 一般都有相同的分布。Validation一般是从Train拆出来的。 随机拆分Train和Tes…
【回归分析】02. 随机向量(2)
文章目录【回归分析】2. 随机向量(2)2.4 正态随机向量的二次型2.5 矩阵微商【回归分析】2. 随机向量(2)
2.4 正态随机向量的二次型
定理 2.4.1:正态随机向量的二次型的方差:
(1) 设 X∼Nn(μ,Σ)X\sim N_n(\mu,\Sigma)X∼Nn(μ,Σ) ,AAA…
多维随机变量及其分布4
(给我学!死劲学!)
目录
一、二维随机变量
1. 定义
2. 二维(多维)联合分布函数的定义
3. 联合分布律 4. 联合概率密度 二、边缘分布
1. 边缘概率密度函数的定义
三、条件分布
1. 条件分布律的定义…
GPS从入门到放弃(十三)、接收机自主完好性监测(RAIM)
接收机自主完好性监测(RAIM: Receiver Autonomous Integrity Monitoring)是根据用户接收机的冗余观测值监测用户定位结果的完好性,其目的是在导航过程中检测出发生故障的卫星,并保障导航定位精度。 为了能进行接收机自主完好性监测…
bandit算法与推荐系统
导语
首先声明,本文基本转载于陈开江先生的《Bandit 算法与推荐系统》一文,加上笔者自己的结合目前推荐项目的理解。不准确之处,愿诸君指正。拜谢。 推荐系统中经常会遇到EE问题和冷启动问题,在笔者项目过程中,无可厚…
概率图降低表示需要的参数指的是什么?(贝叶斯网络) 结构化概率模型
深度学习中经常要对概率密度建模。对于多维度随机变量来说,这有些困难。概率化结构(既图模型)是处理这个问题的手段之一。这引出了两个问题。为什么建模困难?图模型怎样解决了这个困难?
关于这个问题,花书…
《概率论与数理统计》作业一,python画频率分布表
《概率论与数理统计》作业一,python画频率分布表5.12:5:6:5.22:3:5:5.33:4:5:8:10:13:24:28:(1)(2)(3)频率分布表画图函数(按照分割区间大小/按照分组(1)按照分组数(2)按照分割区间大…
概率与信息论基础总结LAN
随机变量: 随机变量(random variable)是可以随机地取不同值的变量 就其本身而言,一个随机变量只是对可能的状态的描述;它必须伴随着一个概率分布来指定每个状态的可能性。 随机变量可以是离散的或者连续的。离散随机变…
卡方检验的基本思想是比较实际观察到的频数与期望的频数之间的差异
卡方检验(Chi-Square Test)是一种用于分析分类数据之间的关联性或独立性的统计方法。它通过比较观察到的数据与预期的数据之间的差异来判断两个或多个变量之间是否存在关联。卡方检验通常用于交叉表格(列联表)的分析,例…
兩隨機變數乘積的期望值
兩隨機變數乘積的期望值以下推導參考Distribution of the product of two random variables - Expectation of product of random variables。 E(XY)E(E(XY∣Y))law of total expectationE(Y⋅E[X∣Y])外層給定Yy,所以Y對內層期望值來說為常數\begin{aligned} \opera…
数学建模系列-优化模型(三)---排队论模型
所谓排队论模型,就是指一个模型中可根据交易简单的需要分为三个部分: (1)顾客造访 (2)服务顾客时间 (3)若不空闲,则顾客需要排队 下面是对于排队论模型的建模以及解决方法…
概率论:条件概率与乘法
条件概率:P(A|B)P(AB)/P(B)为事件A在B发生的条件下的条件概率。
由公式可知:P(AB)P(A|B)P(B),这就是乘法定理,通俗讲就是AB同时发生的概率就是B发生了的概率乘以B发生的情况下A发生的概率。
完备事件组:把样本空间分成几个事件&…
机器学习实战教程(七):朴素贝叶斯
一 简介
朴素贝叶斯算法是有监督的学习算法,解决的是分类问题,如客户是否流失、是否值得投资、信用等级评定等多分类问题。该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。但由于该算法以自变量之间的独立…
概率论:数字特征与极限定理——数学期望
数学期望就是一种平均。 收敛的才有期望。
接下来我们来球一些常见的分布的期望: e^x1x/1x^2/2,泰勒展开。 注意这个是无穷无尽的。
这里使用了一个很巧妙地求和方法。敏锐地发现了k(1-p)^k-1可以变成(1-p)^k的导数,而这个原函数求和是很简…
5328笔记 Advanced ML Chapter6-Sparse Coding and Regularisation
D是Overcompleteness过度完备的 R是Sparsity稀疏的 为什么要稀疏编码,我个人认识是让D尽可能的汇聚更多的信息,它就是一本字典,所以它的信息的超完备的,R是一种检索方式,越稀疏,检索的越快,就好…
GPS从入门到放弃(八)、 GPS卫星速度解算
在阅读这一篇强烈建议先阅读GPS卫星位置解算。为了计算卫星速度,需要对卫星的位置求导。
计算各参变量对时间的导数如下: 计算卫星在轨道平面内的速度 和 WGS-84坐标系中的速度如下: 在之前的位置解算的过程中,我们已经求得了很多…
离散型随机变量及其分布律2
(熟记理解背诵,不管到多少岁!!!都要脱口而出!!!!)
目录
一、三种重要的离散型随机变量
(一)(0-1)分布/两点…
CF618G Combining Slimes 题解
CF618G Combining SlimesCF618G Combining Slimes 首先考虑根据期望的线性性质对于每一个数分开来计算贡献,之后再求出每一个数出现的概率即可。 也不是很清楚这个东西是不是线性性质。 但是说实话就是对于所有数一起考虑是不能入手的。 之后我们发现事实上任意的数…
2021中国大学生程序设计竞赛(CCPC)- 网络选拔赛 1009 Command Sequence HDU - 7108
题目链接
题目大意
给你一个字符串只有UDLR代表一个机器人可以上下左右 问你有多少个字串让机器人运动后可以回到原点
题目思路
机器人运动后回到原点那么 需要保证字串 s(i,j)关于LR和UD的前缀和 一定相等
即sum1[i]-sum1[j-1]0
sum2[…
神经网络是线性模型吗,人工神经网络预测模型
bp神经网络为什么要采用非线性函数来进行预测?
提问:bp神经网络为什么要采用非线性函数来进行预测?回答:简单的讲,主要是复杂的bp神经网络的行为动态及神经元之间的相互作用是无法用简单的线性函数来描述的࿰…
Brain Teaser概率类 - 抛硬币
问题
你有 17 个硬币,我有 16 个硬币,我们同时抛掷所有硬币。 如果你有更多的正面,那么你赢,否则我赢。 你获胜的概率是多少?
解答
划分出3个相互独立的事件:你抛前16枚硬币;我抛16枚硬币&am…
Bayesian Networks ——Stanford CS228
Bayesian Networks
学习一个有效广泛的技术用来参数化概率分布仅仅用少量的参数。通过有向无环图(DAGs)来描述因果模型。研究模型假设和DAG结构之间的关联;不仅模型假设要很清楚,而…
概率统计Python计算:离散型变量独立性判断
随机变量之间的独立性是非常重要的关系。对离散型随机变量XXX,YYY而言,我们知道XXX,YYY独立,当且仅当pijpi⋅⋅p⋅j,1≤i≤m,1≤j≤np_{ij}p_{i\cdot}\cdot p_{\cdot j},1\leq i\leq m, 1\leq j\leq npijpi⋅⋅p⋅j,1≤i≤m…
python科研绘图:P-P图与Q-Q图
目录 什么是P-P图与Q-Q图
分位数
百分位数
Q-Q图步骤与原理
Shapiro-Wilk检验
绘制Q-Q图
绘制P-P图 什么是P-P图与Q-Q图
P-P图和Q-Q图都是用于检验样本的概率分布是否服从某种理论分布。
P-P图的原理是检验实际累积概率分布与理论累积概率分布是否吻合。若吻合…
GPS从入门到放弃(二十五)、卡尔曼滤波
一、概述
单点定位的结果因为是单独一个点一个点进行的,所以连续起来看数据可能出现上串下跳的情况,事实上并不符合实际情况。为了解决这个问题,考虑到物体运动的连续性和运动变化的缓慢性,可以通过滤波器来平滑位置轨迹。 滤波器…
随机变量的分布函数3
(到老也得给我记住!!)
目录
一、分布函数 二、连续型随机变量及其概率密度
三、重要的连续型随机变量
(一)均匀分布
(二)指数分布
(三)正态分布
四、…
随机变量的数字特征5
(学!给我学!)
目录
一、数学期望
二、方差
三、几种重要分布的期望和方差
1. 离散型变量
2. 连续型变量
四、协方差、相关系数
1. 协方差、相关系数的定义
五、矩、协方差矩阵
1. 矩的定义
2. 协方差矩阵的定义 数学…
GPS从入门到放弃(十四)、电离层延时
一、电离层概念
电离层(Ionosphere)是地球大气的一个电离区域。它是受到太阳高能辐射以及宇宙线的激励而电离的大气高层。50千米以上的整个地球大气层都处于部分电离或完全电离的状态,电离层是部分电离的大气区域,完全电离的大气…
C++笔记 蒙特卡罗计算π值
蒙特卡罗 蒙特卡罗(Monte Carlo)方法也称统计模拟方法,是按抽样调查法求取统计值来推定未知特性量的计算方法。 又称随机抽样或统计试验方法。当所求解的问题是某种事件出现的概率,或某随机变量的期望值时,可以通过某种…
ublox f9p,Realsense D435i相关资料
一、Realsense D435i使用笔记
1、Realsense D435i使用笔记
2、Inter Realsense D435i标定详细步骤_高喜天天的博客-CSDN博客
3、Realsense D435i深度测距和普通摄像头单目测距的区别(附带可用实测代码) 4、Realsense D435i学习资料汇总
5、从零开始使用Realsense D435i运行…
假设检验——KS检验、t检验、卡方检验
一、KS检验
1.概述
KS检验是一种非参数的统计检验方法,是针对连续分布(主要用于有计量单位的连续和定量数据)的检验。KS检测常被用来应用于:一是比较单样本是否符合某个已知分布(将样本数据的累计频数分布与特定理论分布相比较,如果两者间差…
2021年电工(初级)考试题库及电工(初级)免费试题
题库来源:安全生产模拟考试一点通公众号小程序
安全生产模拟考试一点通:危险化学品经营单位安全管理人员找解析根据新危险化学品经营单位安全管理人员考试大纲要求,安全生产模拟考试一点通将危险化学品经营单位安全管理人员模拟考试试题进行…
似然(likelihood)和概率(probability)的区别与联系
似然(likelihood)和概率(probability)的区别与联系
https://blog.csdn.net/songyu0120/article/details/85059149
【论文学习笔记2】GaitSpeed: Monitoring and Recognizing Gait Speed Through the Walls
原文链接:https://ieeexplore.ieee.org/document/9003416
1. 其他的
在WiDetect中,作者利用了室内多径环境下电磁波的统计特性,发现:室内有物体运动和无物体运动时,其运动统计量呈现不同的分布特性,且该分…
非独立随机变量的概率上界估计
目前的概率论或者随机变量书籍过分强调对独立随机变量的大数定律,中心极限定理,遗憾上界的估计。而对于非独立随机变量的研究很少,在《概率论的极限定理》中曾给出过一般随机变量求和的渐进分布簇的具体形式,然而形式却太过复杂。…
数学小课堂:统计时有效地筛选数据
文章目录引言I 被爆冷门的原因II 统计时有效地筛选数据2.1 统计数据的常见问题2.2 大数据的特征2.3 有效筛选数据的原则引言
在博弈论中很多结果有发生的概率,而概率这件事只是估计出来的,并不准确。因此,一旦加入博弈的选手多了之后&#x…
概率论与数理统计(2.5)随机变量的函数的分布
随机变量的函数分布一、离散型随机变量函数的分布二、连续型随机变量的函数的分布1.分布函数法解题2.公式法关心的随机变量是某个能直接测量的随机变量的函数,这篇博文将总结如何已知随机变量X的概率分布去求得他的函数Yg(X)(g是连续型函数)的…
sigmoid函数推导过程
1.因为我们逻辑回归是用来做二分类,二分类有个特点就是正例概率负例概率1
所以我们可以将二分类的结果分为0或1,如果随机变量X只取0和1两个值并且相应的概率为
Pr(X1) p,Pr(X0) 1-p, 0<p<1(如果我们数据取1的情况下的概率我们定义成…
机器学习 复习笔记(1) 贝叶斯公式与似然估计
贝叶斯公式: 当x1,x2 …xn对应着不同的theta值。其中一组theta值使得x1, x2…xn发生的概率最大。我们这取这组theta值。这就是极大似然估计。 联合密度函数 注意x1, x2…xn都是已经发生的数据,所以theta才是未知数。似然的意思就是像…的样子…
概率论与数理统计学习:数字特征(二)——知识总结与C语言实现案例
hello,大家好
这里是第11期概率论与数理统计的学习,我将用这篇博客去总结知识点和用C语言实现简单例题的过程。 本期知识点:方差 方差的定义方差的性质几种常用随机变量的方差 💦 知识总结
☁️ 方差的定义
方差刻画了随机变量…
Advanced Predictive Model 知识要点总结2
Content1 Odds and Odds ratioLink function for binary dataOdds Definition2 Is it good fit?For GLM: Deviance DDDFor logistic regression (binomial models):3 Logistic regression classier (逻辑回归分类)ROC 曲线 receiver operating characteristic (ROC) curveAUC4…
Codeforces Round #739 (Div. 3) F2. Nearest Beautiful Number (hard version) 贪心
题目链接
题目大意
给你一个数你需要让这个数字改为另外一个大于等于当前数字的数并且使每一位上独特的数字不超过k个
题目思路
学习了该大佬的思路
从左至右走 每当出现一个未出现过的就将num
若num>k时 就将该位置的数字直到他成为出现过的数字
若他到9,即向前推一…
2021ccpc网络赛重赛
ccpc网络赛重赛Kanade Doesnt Want to Learn CG题目代码Nun Heh Heh Aaaaaaaaaaa题目代码Monopoly题目代码(未完)Kanade Doesn’t Want to Learn CG
题目
就是一道很简单的几何题目,给出下面一个图,其中AC为蓝框,BD为…
Statistical Analysis Plan (SAP) 范例
author: Mingran Jia URL of data: https://nethouseprices.com/house-prices/Lanarkshire/GLASGOW?page1 https://nethouseprices.com/house-prices/Lanarkshire/GLASGOW?page2 … https://nethouseprices.com/house-prices/Lanarkshire/GLASGOW?page10 The context of th…
2021年金属非金属矿山支柱考试题库及金属非金属矿山支柱找解析
题库来源:安全生产模拟考试一点通公众号小程序
安全生产模拟考试一点通:金属非金属矿山支柱考试题库考前必练!安全生产模拟考试一点通每个月更新金属非金属矿山支柱找解析题目及答案!多做几遍,其实通过金属非金属矿山…
算法学习(十九)——A3C
一句话:支持分布式运算的AC
如果理解了AC,理解A3C很容易,没有理论上的创新,主要是工程上效果好。 如图所示,A3C算法通过多个work和环境互动,把环境的梯度给一个全局的网络,也就是通过不同work共…
7、【贝叶斯算法】之实现一个简单的拼写纠正补全器
求解:argmaxc P(c|w) -> argmaxc P(w|c) P© / P(w) P©, 文章中出现一个正确拼写词 c 的概率, 也就是说, 在英语文章中, c 出现的概率有多大P(w|c), 在用户想键入 c 的情况下敲成 w 的概率. 因为这个是代表用户会以多大的概率把 c 敲错成 wargmaxc, 用来枚举所有可…
【概率论】连续型随机变量的分布函数及数学期望(二)
文章目录 填空题 填空题 如果X的密度函数为 p ( x ) { x , 0 ≤ x < 1 ; 2 − x , 1 ≤ x < 2 ; 0 , 其 他 . p(x) \begin{cases} x,&0 \le x<1; \\ 2-x,&1 \le x<2; \\ 0,&其他. \end{cases} p(x)⎩⎪⎨⎪⎧x,2−x,0,0≤x<1;1≤x<2;其他.…
为什么随机误差服从正态分布?
前言正态分布的导出python绘制图像前言正态分布分布在概率论与数理统计中处于核心地位。它最初作为二项分布计算的渐近公式由棣莫弗引进,后被拉普拉斯发展成系统的理论,但把它作为一个分布来进行研究则归功于高斯,他在19世纪初的测量误差研究…
mcq 队列_人工智能能力问答中的人工智能条件概率(MCQ)
mcq 队列1) Which of the following points are valid with respect to conditional probability? Conditional Probability gives 100% accurate results.Conditional Probability can be applied to a single event.Conditional Probability has no effect or relevance or …
【无标题】np.concatenate((n1,n2),axis = 0) 矩阵合并
n1 np.random.randint(1,100,(4,3)) 生成1 -100之间的随机整数 np.vstack((n1,n2)) # 或者(axis 0 表示列) np.concatenate((n1,n2),axis 0)
概率统计Python计算:双正态总体均值差的双侧区间估计
为计算两个正态总体均值差μ1−μ2\mu_1-\mu_2μ1−μ2在指定置信度下的双侧置信区间,涉及样本均值x‾\overline{x}x,y‾\overline{y}y,总体方差σ12\sigma_1^2σ12,σ22\sigma_2^2σ22(或样本方差s22s_2^2s…
概率统计Python计算:单个正态总体均值双侧假设的卡方检验
对正态总体的方差σ2σ02\sigma^2\sigma_0^2σ2σ02进行显著水平α\alphaα下的假设检验,检验统计量n−1σ02S2\frac{n-1}{\sigma_0^2}S^2σ02n−1S2~χ2(n−1)\chi^2(n-1)χ2(n−1)。其中,S2S^2S2为样本方差。用p值法的双侧检验计算函数定义如下。…
5328笔记 Advanced ML Chapter10-Reinforcement Learning
最大化 Expected cumulative reward 期望累计奖励 Q(s0,a0)表示:当状态为s0,做a0的动作,期望累计奖励是Q。 如果我们有n个action,m个state,理论上我们将有nm的Q值。笛卡尔积。 这个表就是Q table。 Q就是在初始…
逻辑回归、深度学习简介、反向传播
Logistic Regression逻辑回归
模型介绍
Logistic Regression 虽然被称为回归,但其实际上是分类模型,并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱。
Logistic 回归的本质是:假设数据服从这个分布&…
2021年危险化学品经营单位安全管理人员找解析及危险化学品经营单位安全管理人员模拟考试题
题库来源:安全生产模拟考试一点通公众号小程序
安全生产模拟考试一点通:危险化学品经营单位安全管理人员找解析根据新危险化学品经营单位安全管理人员考试大纲要求,安全生产模拟考试一点通将危险化学品经营单位安全管理人员模拟考试试题进行…
概率统计Python计算:全概率公式
1. numpy数组的按元素计算
设完备事件组A1,A2,⋯,AnA_1,A_2,\cdots,A_nA1,A2,⋯,An作为引发事件BBB的nnn个因素。诸因素的先验概率构成的序列为P(A1),P(A2),⋯,P(An)P(A_1),P(A_2),\cdots,P(A_n)P(A1),P(A2),⋯,P(An),在诸因素AiA_iAi发生的条件下&a…
离散型随机变量的分布律(也称概率质量函数:probability mass function, PMF)
设是一个离散型随机变量,可能的取值为,取各个值的概率记为: (1)
其中
并且,
公式(1)就称为离散型随机变量的分布律,也称概率质量函数:probability ma…
MarkdownPad2, CSDN及有道云笔记对数学公式的支持
MarkdownPad2, CSDN及有道云笔记对数学公式的支持
MarkdownPad2的安装
下载并安装MrakdownPad2软件,下载地址安装awesomium_v1.6.6_sdk_win, 下载地址安装支持公式编辑的插件,注意,在MarkdownPad2的 Tools > Options > Ad…
算法学习(十八)——Actor Critic
理论上的解释: 强化学习(Reinforcement learning)中Actor-Critic算法该如何深入理解? - 白辰甲的回答 - 知乎 https://www.zhihu.com/question/56692640/answer/289913574 简单解释一下就是:以Policy Gradient算法族中…
pandas计算年化收益波动率
前置:
文章中用到的数据
链接:https://pan.baidu.com/s/1rKLM45dq_xIKxcI54Nq0qg 提取码:c298
公式:
样本标准差公式 年化收益波动率公式 年化收益波动率公式可以转换为【标准差的平方*250,再取平方根】
计算过程…
《遗传算法原理及应用》笔记—绪论
一、绪论
笔者最近在学习遗传算法,希望可以通过笔记对遗传算法做一个简要的介绍与记录。也欢迎小伙伴们一起学习交流。 文章目录一、绪论1.1 遗传算法的生物学基础1.2 遗传算法简介1.2.1 遗传算法概要1.2.2 遗传算法的运算过程1.3 遗传算法的特点1.4 遗传算法的发展…
概率统计Python计算:条件概率和概率乘法公式
1. 古典概型中条件概率的计算
条件概率P(B∣A)P(B|A)P(B∣A)是将样本空间限制在AAA上,A∩BA\cap BA∩B的概率。因此,我们可以利用博文《概率统计Python计算:解古典概型问题》定义的函数P(A, S),计算古典概型中的条件概率。这只需…
概率统计Python计算:单个正态总体均值的双侧区间估计
我们知道,计算单个总体XXX~N(μ,σ2)N(\mu,\sigma^2)N(μ,σ2)的参数μ\muμ对给定置信水平1−α1-\alpha1−α的置信区间,除了置信水平外,还需要如下几个要素:样本均值x‾\overline{x}x,样本方差s2s^2s2或总体方差σ2…
用Scipy求解单个正态总体的置信区间
区间估计简介Python求解单个正态总体参数的置信区间参考区间估计简介假定参数是射击靶上 10 环的位置,作一次射击,打在靶心 10 环的位置上的可能性很小,但打在靶子上的可能性就很大,用打在靶上的这个点画出一个区间,这…
统计学学习日记:L8-参数估计
目录
一、估计量与估计值
二、评估统计量的标准
三、点估计
四、区间估计 一、估计量与估计值
1.估计量:用于估计总体参数的随机变量 如样本均值、样本比例、样本方差等 例如:样本均值就是总体均值μ的一个估计量
2.参数用θ表示,估计…
概率论与数理统计 期末突击复习
概率论与数理统计第一章 概率论的基本概念第二章 随机变量及其分布第三章 多维随机变量及其分布第四章 随机变量的数字特征第五章 大数定律和中心极限定理第六章 样本及其抽样分布第七章 参数估计第八章 假设检验第一章 概率论的基本概念 q1 考点 q 考点 q 考点 q …
指数平滑方法(一次指数平滑、二次指数平滑、三次指数平滑):理论、代码、参数 介绍(全)
创建于:20210324 修改于:20210324 文章目录特别说明参考来源包版本号1、简介2、一次指数平滑2.1 理论介绍2.2 代码展示2.3 参数介绍3、 二次指数平滑3.1 理论介绍3.1.1 Holt’s linear trend method3.1.2 Damped trend methods3.2 代码展示3.3 参数介绍4…
深度学习用于医学预后-第二课第三周4-7节-关于事件的时间数据,认识处理删失数据
在本课中,我们将讨论生存数据。为了能够对生存进行建模,我们需要能够以我们可以处理的形式表示数据。
主要的挑战是删失数据,这是一种特殊形式的缺失数据。我们接下来将要研究这一点。
在这节课中,我们将谈论生存数据和删失。
…
【论文学习笔记1】WiDetect: Robust Motion Detection with a Statistical Electromagnetic Model
原文链接:https://dl.acm.org/doi/10.1145/3351280
0.概括
与以前提取以数据为导向的特征、或假设一些反射多路径的方法不同,本文通过考虑室内所有多路径的情况,从电磁波的统计理论的角度来对问题进行建模。利用电磁波的统计理论࿰…
TD算法超详细解释,一篇文章看透彻!
【已解决】TD算法超详细解释和实现(Sarsa,n-step Sarsa,Q-learning)一篇文章看透彻! 郑重声明:本系列内容来源 赵世钰(Shiyu Zhao)教授的强化学习数学原理系列,本推文出于非商业目的分享个人学习…
tf中的Auto Encoder(AE和VAE)
tf中的Auto Encoder(VAE) 文章目录tf中的Auto Encoder(VAE)1. Auto Encoder(AE)2. Variational Auto Encoder(VAE)3. AE实战VAE实战1. Auto Encoder(AE)
基本…
spark-shell报错:Version information found in metastore differs 2.3.0 from expected schema version1.2.0
在spark-shell执行如下语句时候
scala> spark.sql("show tables").show
报错: Version information found in metastore differs 2.3.0 from expected schema version 1.2.0. Schema verififcation is disabled hive.metastore.schema.verification …
深度学习数学基础1_函数与极限
一、极限的公理化定义
如果任意伊布舍隆,总是存在一个正数德尔塔,当0<|x-x0|<德尔塔时,总有|f(x)-A|<伊布舍隆,则
f(x)的极限为A。
Java 1013 数素数
题目内容:
令 Pi 表示第 i 个素数。现任给两个正整数 M≤N≤104,请输出 PM 到 PN 的所有素数。
输入格式:
输入在一行中给出 M 和 N,其间以空格分隔。
输出格式:
输出从 PM 到 PN 的所有素数࿰…
Java中BigDecimal类
BigDecimal类介绍
Java中提供了大数字(超过16位有效位)的操作类,即 java.math.BinInteger 类和 java.math.BigDecimal 类,用于高精度计算. 其中 BigInteger 类是针对大整数的处理类,而 BigDecimal 类则是针对大小数的处理类. BigDecimal 类的实现用到了 BigInteger类,…
pandas.DataFrame.sample函数抽样划分Pascal voc数据 训练集验证集测试集
先查sample函数的使用方法 DataFrame.sample(nNone, fracNone, replaceFalse, weightsNone, random_stateNone, axisNone)[source] DataFrame可以是Series、DataFrame 其中的n和frac是相同的作用,n的含义是抽样的个数,是整数;frac是浮点…
[解题报告]《算法零基础100讲》(第1讲) 幂和对数
☘前言☘
今天是算法零基础打卡的第1天,大家先熟悉一下感觉,课后题我给大家亿点点参考。上链接: 《算法零基础100讲》(第1讲) 幂和对数 🧑🏻作者简介:一个从工业设计改行学嵌入式的年轻人 ✨联系方式&…
统计学学习日记:L1-样本、总体和变量
一、统计数据类型
1.1 按计量尺度划分
1.1.1 分类数据
能归于某一类别的非数字型数据,是对事物进行分类的结果,,数据表现为类别,是用文字来描述。
如人口按照性别划分为男,女;企业按行业属性划分为医药…
统计学学习日记:L3-集中趋势分析之平均数
目录
一、平均数
二、算术平均数
三、加权平均数
四、几何平均数 一、平均数
1.也称为均值
2.集中趋势的最常用测度值
3.一组数据的均衡点所在
4.体现了数据的必然性特征
5.易受极端值的影响
6.有简单平均数和加权平均数之分
7.根据总体数据计算的,称为…
统计学学习日记:L6-离散趋势分析之总体方差和标准差
目录
一、数据型数据:方差和标准差
1.1 总体方差与标准差
1.1.1 方差的公式 1.1.2 标准差的公式
1.2 样本方差与标准差
1.2.1 方差的公式
1.2.2 标准差的公式
二、自由度
三、相对位置的度量:标准分数
四、度量相对离散程度:离散系数…
统计学学习笔记:L1-总体、样本、均值、方差
目录
一、总体和样本
二、集中趋势分析
2.1 均值
2.1.1 样本均值
2.1.2 总体均值 2.2 众数,中位数
三、离散趋势分析
3.1 总体方差
3.2 样本方差
3.3 标准差 一、总体和样本
比如要计算全国男性的平均身高,但是全部调查是不现实的,…
ppt学习日记:L2-文字与字体
目录
一、精简文案的三步骤 二、让文案表达更有趣
2.1 反转法
2.2 悬念法
2.3 谐音法
三、保存特殊字体
3.1 字体矢量化(给文字布尔运算,首选方案)
3.2 字体转为图片
3.3 嵌入字体
3.4 图片演示文稿 一、精简文案的三步骤
拆&#…
简单多层全连接神经网络
1.简单多层全链接前向网络
1.1模拟神经元 脑神经元收到一个输入的信号,经过不同的突触、信号进入神经元,接着通过神经元内部的激活处理,最后沿着神经元的轴突输出一个信号,这个轴突通过与下一个神经元的突触相连,从而…
学习模式上的记录之统计篇三 置换检验 Permutation Test
偶然间看到有人用置换检验,上午看了下基础的讲解,先记录下来以便于自己理解。 讲解内容最初看的是这个网站 置换检验可视化讲解
置换检验是一种非参数检验,也就是对数据的分布、方差等没有要求。
复习 可能有些小同志看到这里不太清楚什么是…
数理统计:样本及抽样分布7
(几天没学习了?好好反省反省!!卷起来)
目录
一、随机样本
二、直方图
三、箱线图
四、抽样分布
五、重要的分布
1. 卡方分布
2. t 分布
3. F 分布 在概率论中,对于随机变量的分布都是已知的&…
【概率论】随机变量的方差与标准差作业
文章目录 选择题 选择题 设随机变量X服从区间(-1,2)上的均匀分布,则D(X)() A.1/4 B.1/2 C.3/4 D.1/8 【正确答案:C】 把红、黄、白3个小球随机地放入两个杯子中,若设X为有小球的杯子数,则D(X)(…
基于2022高考数学全国卷I概率题解题思路初步分析新冠病毒疫苗
基于2022高考数学全国卷I概率题解题思路初步分析新冠病毒疫苗1. 2022高考数学全国卷I概率题2. 卡方(χ2\chi^2χ2)检验原理回顾3. 解答2022高考数学全国卷I概率题4. 上海疫情分析5. 总结1. 2022高考数学全国卷I概率题 一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯…
似然函数与极大似然估计
似然函数与极大似然估计
标签(空格分隔): ML
似然函数 随机变量XXX的概率分布已知,但是这个分布的参数是未知的,需要我们去估计,我们把他记作θ\thetaθ,好比在抛硬币的试验中,硬币…
考研数学历程(九月)
9.6日开始 4h学习法
九月部分
第一天
P3 1.对数函数定义 √ 2.对数图像 √
P4 1.关于绝对值的正负号 2.复合函数定义及书上f(x)和f(g(x))类型题目解惑 P5 1.反函数4.5性质理解和证明 √ P6 1.各类函数图像画出 还有正哥和宇哥…
状压dp、数位dp、概率dp
裁玻璃
#include<bits/stdc.h>
#define intn long long
using namespace std;
int dp[1100][1100],a[1100],s[1100];
int getsum(int s)
{int res0;while(s){if(s&1)res;s>>1;}return res;
}
int judge1(int s1,int sd)
{if((s1&sd)||(s1<<1)&s…
【概率论】期末复习笔记:假设检验
假设检验目录一、假设检验的基本概念1. 假设检验的基本原理2. 两类错误3. 假设检验的一般步骤4. ppp值二、正态总体参数的假设检验σ2已知,检验μ与μ0的关系\color{dodgerblue}\sigma^2\text{已知,检验}\mu\text{与}\mu_0\text{的关系}σ2已知ÿ…
Probability Density Reweight
Probability Density Reweight
Reweight 是通过将采样样本乘以 reweight 权重,从而将样本从原始密度 P0P_0P0 转移至新密度 P1P_1P1 的方法。 当从原始密度采样样本 xxx 时,xxx 的期望为 Ex∼P0[x]∫P0(x)xdx≈1N∑ixi(1)E_{x \sim P_0}[x] \int P…
求和中x:y=g(x)的含义
概念解释 p ( y ) ∑ x : y g ( x ) p ( x ) p(y)\sum\limits_{x:yg(x)}p(x) p(y)x:yg(x)∑p(x)
这个表达式表示随机变量 Y 的概率分布 p(y) 是通过对随机变量 X 进行函数映射 y g ( x ) y g(x) yg(x) 后得到的。让我更详细地解释: Y Y Y 和 X X X 是两个随…
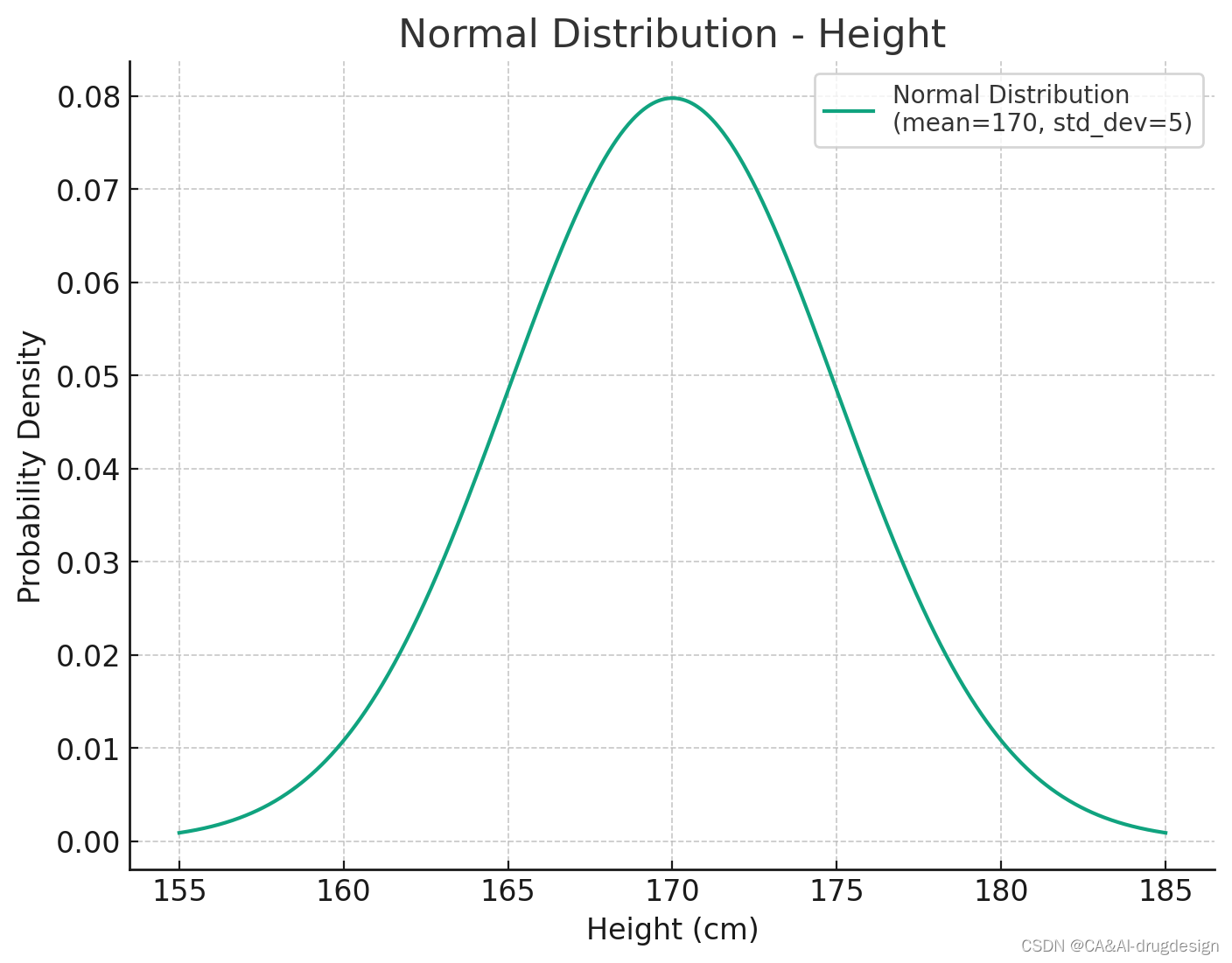
概率密度函数(PDF)正态分布
概率密度函数(PDF)是一个描述连续随机变量取特定值的相对可能性的函数。对于正态分布的情况,其PDF有一个特定的形式,这个形式中包括了一个常数乘以一个指数函数,它假设误差项服从均值为0的正态分布: p ( …
贝叶斯算法+贝叶斯实践
贝叶斯分析
一般用于新闻分类、评论分析
数理统计基本概念 贝叶斯定理 举例 朴素贝叶斯 多项式模型 伯努利模型 混合模型 高斯模型
# 导入算法包以及数据集
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_sp…
看见统计——第四章 统计推断:频率学派
看见统计——第四章 统计推断:频率学派
接下来三节的主题是中心极限定理的应用。在不了解随机变量序列 {Xi}\{X_i\}{Xi} 的潜在分布的情况下,对于大样本量,中心极限定理给出了关于样本均值的声明。例如,如果 YYY 是一个 N(0&am…
GPT和GPT2结构的区别
GPT1结构图如下所示: GPT2结构图如下: 注意,GPT2的最后一个LayerNorm在24个transformers或是12个transformers结构之后添加的, 这里layernormalization放在前面类似于预激活函数的设定,在另外一篇文章Identity mapping…
概率论与数理统计(4.2)方差的基础知识来复习一下?
文章目录一、随机变量方差1.概念2.计算定义计算公式计算3.性质4.标准化变量二、重要概率分布的方差三、切比雪夫不等式一、随机变量方差
1.概念
定义: 意义: 表达了X的取值与其数学期望的偏离程度。值小则比较集中在E(X)附近,值大则比较分…
概率论与数理统计(4.1)数学期望
文章目录离散型1、离散型随机变量的数学期望例1例22、离散型随机变量函数的数学期望例33、二维离散型随机变量函数的数学期望例4连续型1、连续型随机变量数学期望例42、连续型随机变量函数的数学期望例53、二维连续型随机变量函数的数学期望数学期望的重要性质例6常见分布的数学…
统计学习方法 EM 算法
文章目录 统计学习方法 EM 算法引入EM 算法EM 算法的导出EM 算法的收敛性三硬币模型 统计学习方法 EM 算法
学习李航《统计学习方法》时关于 EM 算法的笔记
引入
概率模型中有时候同时包含观测变量(observable variable)和隐变量(潜在变量…
常见不等式考察(一)——Jensen不等式
常见不等式考察(一)——Jensen不等式 0. 引言1. Jensen不等式定义2. Jensen不等式证明3. Jensen不等式的常见形式 1. 具体凸函数下的Jesen不等式 1. 幂函数2. 对数函数3. 指数函数4. 三角函数 2. 连续形式下的Jensen不等式3. 概率论中的Jensen不等式 4. …
【机器学习理论】L1 热身和中心极限定理
缩写 IID:独立同分布(Independent Identically Distribution)PDF:概率密度函数(probability density function)CLT:中心极限定理(central limit Theorem)CDF:…
数值分析(9):数值积分之Newton-Cotes求积公式和复合求积公式
数值积分之Newton-Cotes求积公式和复合求积公式1. Newton-Cotes求积公式1.1 N-C求积公式的推导1.2 N-C求积公式的余项1.3 N-C求积公式的数值稳定性2. 复合求积公式2.1 复合梯形求积公式2.2 复合Simpson求积公式1. Newton-Cotes求积公式
1.1 N-C求积公式的推导
在《数值分析(8…
概率统计Python计算:一元线性回归未知参数的点估计
设试验结果可表为随机变量YYY,影响试验结果YYY的因素是可控的且表为普通变量xxx,若YYY~N(axb,σ2)N(axb,\sigma^2)N(axb,σ2),其中a,ba,ba,b即σ2\sigma^2σ2均为未知参数。对xxx的一系列取值(x1,x2,⋯,xn)(x_1,x_2,\cdots,x_n)(x1,x2,⋯…
概率图模型--变量消元法与团树传播算法
概率图模型–变量消元法与团树传播算法 – 潘登同学的Machine Learning笔记 文章目录概率图模型--变量消元法与团树传播算法 -- 潘登同学的Machine Learning笔记简单回顾概率图模型的推理任务变量消元算法MRF应用变量消元算法贝叶斯网络应用变量消元算法消元顺序1(没有固定的说…
5328笔记 Advanced ML Chapter8-Domain Adaptation and Transfer Learning
5328始终要记住全局和样本是不同的。这是关键。 当我们说2个任务不同时,其实是说它们的全局数据分布不同。如果2个任务有相同的全局数据分布,那么我们可以使用相同的算法去解决它们。 数据的概率分布就是domain。 机器要想做相同知识的学习&…
学习不同概率分布(二项分布、泊松分布等)概念及基础语法
概率分布是描述随机变量取值的概率情况的函数。常见的概率分布包括二项分布、泊松分布等。 二项分布(Binomial Distribution):描述了一次试验中成功事件发生的次数的概率分布。它的基础语法如下: 概率质量函数:pmf(k, …
概率论小课堂:概率简史(从不确定到确定,再到不确定。)
文章目录 引言I 概率论起源1.2 掷骰子游戏1.1 算牌II 拉普拉斯定义了古典的概率公式2.1 单位事件2.2 古典的概率公式2.3 必然事件2.4 不可能事件2.5 古典的概率公式的漏洞引言
从不确定到确定的过程: 几何学通过几个公理和逻辑推演,认识到很多定理。在代数学中,求出方程的解…
《统计学习方法》习题答案
第一章 统计学习及监督学习概论
课后习题 1.1 说明伯努利模型的极大似然估计以及贝叶斯估计中的统计学习方法三要素。伯努利模型是定义在取值为0与1的随机变量上的概率分布。假设观测到伯努利模型n次独立的数据生成结果,其中k次的结果为1,这时可以用极大…
T检验两个函数stats.t.cdf和stats.t.sf(左尾/右尾T检验)
左右T检验都是用于比较两组数据之间的差异,但它们的应用场景和假设略有不同。 左尾T检验(One-tailed T-test)用于检查一个样本是否显著地小于另一个样本。它的零假设是一个样本的平均值小于或等于另一个样本的平均值。 右尾T检验(…
中国人民大学与加拿大女王大学金融硕士——在职人员成长路上的选择与追求
在职人员职场充电,选择中国人民大学与加拿大女王大学金融硕士项目是正确的吗?其实每个选择都有各自的收获和代价,不能简单的用“优劣”、“好坏”去衡量。要看这个选择是否给给予你想要的,还要看这个选择的代价是否是你愿意承受并…
基于物品的协同过滤推荐笔记(附源代码)
基于物品的协同过滤算法
1. 数据
使用movielens-100k数据集中的u1.base文件作为实验集
2.实验
在demo1中建立用户-评分矩阵和用户看过的电影id列表,根据用户看过的电影计算电影间相似度,根据项亮的《推荐系统实践》中方法计算用户相似度。 相似度公式…
2021中国大学生程序设计竞赛(CCPC)- 网络选拔赛 1007 Function HDU - 7106 数学思维+二分
题目链接 Problem Description Lets define the sum of all digits in x as g(x). For example, g(123)1236. Give you a function: f(x)Ax2g(x)Bx2Cxg2(x)Dxg(x) Find the minimum value of f(x), where x is an integer and 1≤x≤N. 题目大意
给出如题意的函数 让你求函数最…
为什么高斯白噪声的平均功率等于方差?
功率和方差这两个概念,一个是表示信号的强度,一个是表示随机信号的一个统计量,为什么高斯白噪声的平均功率会等于它的方差呢?什么是高斯白噪声?维基百科上给出的解释是:在通信领域中指的是一种功率谱函数是…
切比雪夫不等式 大数定律 中心极限定理
本篇为《深度学习》系列博客的第五篇,该系列博客主要记录深度学习相关知识的学习过程和自己的理解,方便以后查阅。
上篇博客说道"均值和期望的联系是大数定理联系起来的‘,这里这里看到一篇博客讲解了基本的极限定理,这里做…
瑞利分布(Rayleigh Distribution)回顾
瑞利分布(Rayleigh Distribution)回顾背景瑞利分布信道增益的计算信道产生待完善和整理参考链接背景
瑞利衰落被认为是对流层和电离层信号传播以及城市密集环境对无线电信号影响的合理模型。瑞利衰落是一种统计模型,该模型假设已经通过该传输…
概率统计Python计算:连续型随机变量函数分布
我们知道,对XXX已知的分布函数FX(x)F_X(x)FX(x),若函数Yg(X)Yg(X)Yg(X)具有单调增加的反函数Xg−1(Y)Xg^{-1}(Y)Xg−1(Y),则YYY的分布函数FY(y)FX(g−1(y)F_Y(y)F_X(g^{-1}(y)FY(y)FX(g−1(y)。在Python中,我们也可以通过这…
概率统计Python计算:连续型自定义分布数学期望的计算(二)
对联合密度函数为f(x,y)f(x,y)f(x,y)的2-维连续型随机向量(X,Y)(X,Y)(X,Y),下列代码定义计算其函数Zg(X,Y)Zg(X,Y)Zg(X,Y)的数学期望E(g(X,Y))E(g(X,Y))E(g(X,Y))的Python函数。
from scipy.integrate import dblquad #导入dblquad
def expectcont2(pdf, f…
机器学习的几种分类损失函数
1. 机器学习的几种分类损失函数
1.1 信息量
信息量也叫做香农信息量,常用于刻画消除随机变量X在x处的不确定性所需的信息量\color{red}刻画消除随机变量X在x处的不确定性所需的信息量刻画消除随机变量X在x处的不确定性所需的信息量。假设连续型随机变量࿰…
WS小世界网络度分布公式推导
假设网络中度数为 k k k 的节点有 N k N_k Nk 个,总共有 N N N 个节点,则度数为 k k k 的节点出现的概率可以表示为: P ( k ) N k N P(k) \frac{N_k}{N} P(k)NNk
由于在WS小世界网络中,每个节点的度数都是 k k k&am…
威尔·库尔特《趣学贝叶斯统计:橡皮鸭、乐高和星球大战中的统计学》学习笔记(1):以A/B测试为例学习贝叶斯统计
主要是新学期的概率论的作业要求:Write a summary (no more than of a page) of your experience with an application of probability to a real-life situation (e.g., an engineering problem.
–How was probability used to model the phenomena/situation?…
Normal Distribution Chi-squared Distribution t distribution F-distribution
最近看论文发现经常有一些统计学的内容,但是这部分内容之前一直都是很薄弱的地方,不敢涉猎,现在学习一下,并整理下来,方便以后查阅。 Normal Distribution & Chi-squared Distribution & t distribution &…
3.4 随机变量的相互独立性
学习目标:
要学习二维随机变量的相互独立性,我会按照以下步骤进行: 学习独立性的概念:在概率论中,两个事件A和B是相互独立的,当且仅当它们的概率乘积等于它们的联合概率,即P(A∩B)P(A)P(B)。将…
期望值、方差、协方差、相关系数,numpy 计算均值、方差、协方差,相关系数
文章目录期望值、方差、协方差、相关系数一、期望值二、方差1. 概念:2. 示例:三、协方差1. 概念:2. 示例:四、协方差矩阵1. 概念:2. 示例:五、协方差的相关系数1. 概念:2. 示例:六、…
概率论:数理统计基本概念——三大分布
首先是X分布: n1的时候,f(y)就是正态分布平方的密度函数,这个可以用yg(x)的密度函数计算方法来计算。
自由度是什么?: 很显然,几个X加起来,也就是自由度加起来: 接下来是t型分布&am…
机器学习算法理论:贝叶斯
贝叶斯定理对于机器学习来说是经典的概率模型之一,它基于先验信息和数据观测来得到目标变量的后验分布。具体来说,条件概率(也称为后验概率)描述的是事件A在另一个事件B已经发生的条件下的发生概率,公式表示为P(A|B)&a…
方差与协方差之间的区别?
方差和协方差都是用来衡量随机变量之间关系的统计量,但它们的计算方式和含义有所不同。 方差(Variance):方差是描述数据集合离散程度的统计量,它衡量了数据点与均值之间的平均距离。 方差越大,表示数据点越…
【计量经济学】时间序列回归的渐进性
时间序列回归的渐进性 --潘登同学的计量经济学笔记 文章目录时间序列回归的渐进性 --潘登同学的计量经济学笔记平稳与弱相关平稳过程协方差平稳平稳性有什么用?弱相关时间序列平稳与弱相关的误区OLS的渐进性假定TS.1假定TS.2假定TS.3OLS的一致性举个例子假定TS.4假定…
概率论与数理统计中常见的随机变量分布律、数学期望、方差及其介绍
1 离散型随机变量
1.1 0-1分布
设随机变量X的所有可能取值为0与1两个值,其分布律为 若分布律如上所示,则称X服从以P为参数的(0-1)分布或两点分布。记作X~ B(1,p)
0-1分布的分布律利用表格法表示为:
X01P1-PP
0-1分布的数学期望E(X) 0 *…
20230702 正态分布的几个性质
正态分布以及高斯函数的定义
如果随机变量 X X X 的密度函数为 f μ , σ ( x ) 1 σ 2 π e − ( x − μ ) 2 2 σ 2 , x ∈ R , σ > 0 f_{\mu, \sigma}(x)\frac{1}{\sigma \sqrt{2 \pi}} e^{-\dfrac{(x-\mu)^2}{2 \sigma^2}}, \quad x \in \mathbb{R}, \sigma>0 …
【推荐系统->统计学】辛普森悖论(Simpson‘s paradox)
辛普森悖论
辛普森悖论(Simpson’s paradox),也有其他名称,是概率和统计中的一种现象,即一种趋势出现在几组数据中,但当这些组组合在一起时,趋势就会消失或逆转。 这个结果在社会科学和医学科学统计中经常遇到&#x…
风水——概率学——需要大数据依托
首先,什么是科学?
科学,就是被证实客观存在的普遍现实,但它并不代表,没有被证实的事物,就是伪科学。相反,现有的科学,却很有可能是伪科学,就像曾经的地心说,…
机器学习100天(三十七):037 朴素贝叶斯-挑个好西瓜!
《机器学习100天》完整目录:目录 机器学习100天,今天讲的是:朴素贝叶斯-挑个好西瓜!
红色石头已经了解了贝叶斯定理和朴素贝叶斯法,接下来已经可以很自信地去买瓜了。买瓜之前,还有一件事情要做,就是搜集样本数据。红色石头通过网上资料和查阅,获得了一组包含 10 组样…
策略梯度中的baseline
策略梯度中的Baseline
Policy Gradient with Baseline
Policy Gradient
策略梯度是关于策略网络的参数求的,策略网络π(a∣s;θ)\pi (a|s;\theta)π(a∣s;θ)的参数是θ\thetaθ,我们使用策略网络来控制Agent做运动。状态价值函数Vπ(s)V_{\pi}(s)Vπ…
用二元泊松模型预测2022世界杯8强
用二元泊松模型预测2022世界杯8强
网上有很多文章用双泊松(Double Poisson)模型来预测世界杯比赛结果。但是双泊松模型有一个严重的缺陷,那就是它假设比赛中两队的比分是条件独立的。而我们都知道,在对抗性比赛中,两…
数学建模系列-优化模型(五)---遗传算法模型
什么是遗传算法?遗传算法和模拟退火可以说是数学建模系列中两个万金油的角色, 只要有一定的原理知识,我们就可以对其进行判断。
但是一般情况下给的分都不会特别高,毕竟数学建模比赛主要考察的还是对于数学基础的。
遗传算法&am…
零基础掌握“全概率公式”
目录一.举例子引出全概率公式二.条件概率表示全概率公式(更常用)一.举例子引出全概率公式
案例一: 如果想判断刘阳是否是高个子概率,也么对于正常的人类来说,也许只有如下三种情况: ①刘阳是一个高个子的男…
F(X)分布函数的通俗解释
爱心大纲一.分布函数的定义二.分布函数的通俗解释一.分布函数的定义
分布函数的定义: 其实分布函数所求出的东西是“概率”,在x取某个值时这个事件所发生的概率,即可能性是多大。 二.分布函数的通俗解释
以身高为例子;
假设世…
概率论:参数估计——点估计
首先,我们要知道点估计是什么: 简单来讲,点估计一般就是拿出很多样本来,拿他们的均值和方差之类的当成参数,或者是通过均值和方差计算出他的参数。 简单来说,参数空间就是这个分布的参数可以的取值。 先学习…
09-09-头条01
文章模型
任何互联网产品的通用用户画像:很抠,脾气很坏,耐心很差。 1自媒体文章
总:综述
分:并列分论点图
总:总结引导互动
个人成长,职场类文章 情感类,励志类文章
简书上的爆款文章
励…
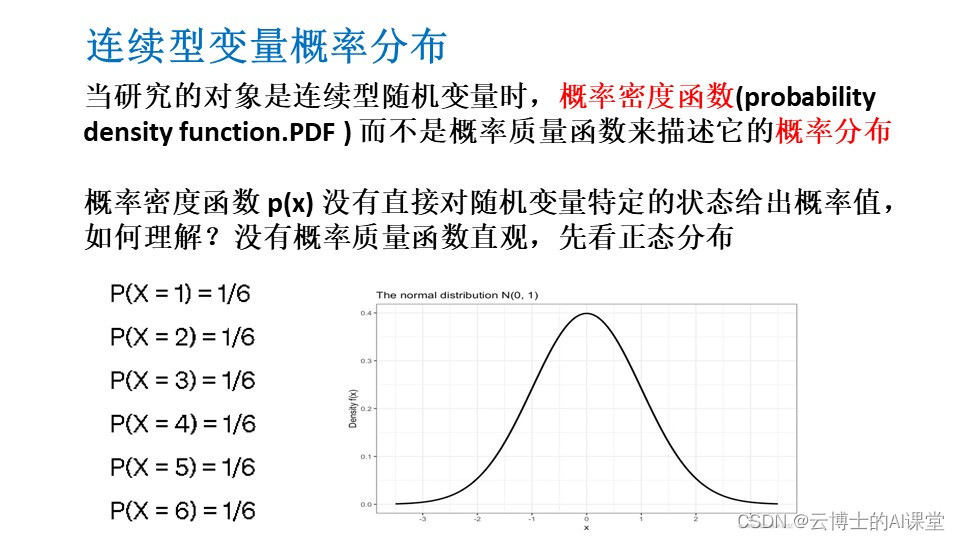
理解概率分布函数和概率密度函数
离散型随机变量和连续性随机变量 如果随机变量的值都可以逐个列举出来,则为离散型随机变量。如果随机变量X的取值无法逐个列举则为连续型变量。 进一步解释,离散型随机变量是指其数值只能用自然数或整数单位计算的则为离散变量。例如,企业个数…
PT_二维连续型随机变量(二维均匀分布/二维正态分布)
文章目录二维连续型随机变量联合密度的性质边缘密度函数二维均匀分布例二维正态分布二维连续型随机变量 设二维随机变量(X,Y)的分布函数为F(x,y) 如果存在一个非负可积函数f(x,y),对于任意的实数x,y如果存在一个非负可积函数f(x,y),对于任意的实数x,y如果存在一个非负可积函数f…
5328笔记 Advanced ML Chapter11-Causal Inference
辛普森悖论的原因是样本数量不匹配。TreatmentA对大小结实治愈率都高过TreatmentB,但是总的治愈率却低于B。 当添加了Age后,biking和cholesterol的关系从正相关变为了负相关。 correlation正相关,causation因果关系 从上面冰激凌的例子…
第四章朴素贝叶斯法.4.3 期望风险最小化
文章目录后验概率最大化推导本课程来自深度之眼,部分截图来自课程视频以及李航老师的《统计学习方法》第二版。公式输入请参考:
在线Latex公式后验概率最大化
后验概率最大化等价于期望风险最小化 已知条件: 假设朴素贝叶斯使用0-1损失函数&…
概率论与数理统计 知识点+课后习题
文章目录 💖 [学习资源整合](https://www.cnblogs.com/duisheng/p/17872980.html)📚 总复习📕 知识点⭐ 常用分布的数学期望和方差 📙 选择题📙 填空题📙 大题1. 概率2. 概率3. 概率4. P5. 概率6. 概率密度…
Nakagami-m分布、Gamma分布的无线信道及Python代码
Nakagami-m分布无线信道中产生分布为Nakagami的信道Nakagami-m分布特征1、概率密度函数PDF(Probability Density Function)2、累积密度函数CDF(Cumulation Density Function)4、无线信道参数设计5、综合各函数表Gamma分布代码1、验…
概率大揭秘:深度复习概率论,事半功倍的学霸秘籍!
第一章 概率论的基本概念
一、事件及其关系与运算 1、样本空间、样本点、随机事件、必然事件、不可 能事件、基本事件和复合事件的概念; 2、事件的包含与相等:若事件A包含事件B,则B的发生必然导致A的发生。进而有P(AB)P(B),P…
Struggle to 搞懂统计学——点估计 区间估计 置信区间
文章目录点估计区间估计置信区间理解操作(重中之重)总体方差已知总体方差未知假设检验在统计学的应用过程中,总有那么几个重要的基础概念似懂非懂,就像雾里看花,你对它有一个总体的印象,但说道具体细节又似…
团体程序设计天梯赛训练题目集 7-11 N个数求和 (20 分)c语言实现
本题的要求很简单,就是求N个数字的和。麻烦的是,这些数字是以有理数分子/分母的形式给出的,你输出的和也必须是有理数的形式。
输入格式:
输入第一行给出一个正整数N(≤100)。随后一行按格式a1/b1 a2/b2 …
Python入门知识点分享——(十六)标准库的导入和调用
在正式学习面向对象编程之前,我们先讲一下怎么在代码中导入并调用现成的模组,也就是Python中的标准库。像我们之前介绍过的os模块就是其中之一,下面我将为大家分别介绍几个常用的标准库。
math
math 模块提供了许多对浮点数的数学运算函数&…
1.5 全概率公式和贝叶斯公式
1.5.1 全概率公式在处理复杂事件的概率时,我们经常将这个复杂事件分解为若千个互不相容的较简单的事件之和,先求这些简单事件的概率,再利用有限可加性得到所求事件的概率,这种方法就是全概率公式的思想方法全概率公式是概率论中的一个非常重要…
Fast Global Registration
文章目录3两个点云配准3.1目标函数3.2优化3.3对应关系4多个点云配准4.1目标函数4.2优化3两个点云配准
3.1目标函数
对于俩个点集PPP和QQQ,我们的目的是找到一个刚体变换,对齐这两个点集。我们的方法是优化关于PPP和QQQ对应关系的稳健性目标函数。 设K(…
计算机视觉与模式识别概念
模式:相同或相似的事物,要被识别的对象的数字化
模式类:相同或相似事物的全体(概率里的总体)
模式样本:对具体事物观测的观测数据
模式分布:大量观测获取的分布
模式识别:用计算机实现人类对…
随机过程 Markov 链(上)
文章目录随机过程 Markov 链(上)基本概念n 步转移概率 C-K 方程状态的分类及性质随机过程 Markov 链(上)
基本概念
有一类过程,具备所谓的 ”无后效性“(Markov 性),即要确定过程将…
概率论:数字特征与极限定理——协方差与相关系数
这就是协方差的起源。原本是求D(xy)D(x)D(y)2E(x-E(x))E(y-E(y)) ,后面的小老弟翻身做主人了。当然最后常用的公式是E(XY)-E(X)E(Y)
当XY时,这个公式就是方差公式。 刚刚的问题,在这里直接用公式回答了。
最后的定理可以用性质4和3推出来。…
SPSS两独立样本的非参数检验
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件请点击此链接下…
python实现two way ANOVA
文章目录 目的:用python实现two way ANOVA 双因素方差分析1. python代码实现1 加载python库2 加载数据3 统计样本重复次数,均值和方差,绘制箱线图4 查看people和group是否存在交互效应5 模型拟合与Two Way ANOVA:双因素方差分析6 …
【机会约束、鲁棒优化】机会约束和鲁棒优化研究优化【ccDCOPF】研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…
【概率论】贝叶斯公式的作业
文章目录 填空题填空题 两台车床加工同样的零件,第一台出现不合格品的概率是 0.03,第二台出现不合格品的概率是 0.06,加工出来的零件放在一起,并且已知第一台加工的零件比第二台加工的零件多一倍.如果取出的零件是不合格品,求它是由第二台车床加工的概率_____; (结果小数点…
Part 4 描述性统计分析(占比 10%)——上
文章目录【后续会持续更新CDA Level I&II备考相关内容,敬请期待】【考试大纲】【考试内容】【备考资料】1、统计基本概念1.1、统计学的含义及应用1.1.1、统计学的含义1.2.1、统计学的应用1.2、统计学的基本概念1.2.1、数据及数据的分类1.2.2、总体和样本1.2.3、…
常用 - 现代希腊字母对应代码
序号字母大写字母小写对应代码汉语读法1A\AlphaAα\alphaα\alpha阿尔法2B\BetaBβ\betaβ\beta贝塔3Γ\GammaΓγ\gammaγ\gamma伽玛4Δ\DeltaΔδ\deltaδ\delta德尔塔5Eε\varepsilonε\varepsilon埃普西隆6Z\ZetaZζ\zetaζ\zeta泽塔7H\EtaHη\etaη\eta伊塔8Θ\ThetaΘθ\…
R/d2及S/C4估计总体标准差,比较其CPK及规格限概率的差异
R/d2 和 S/C4 是用于估计总体标准差的无偏估计方法,通常用于控制图中。这些估计方法的主要目的是通过样本数据来估计总体标准差,以便监测过程的稳定性和变异性,而不需要收集整个总体的数据。
具体来说:
R图中的 R/d2 和 S图中的…
现代密码学基础(2)
目录
一. 介绍
二. 举例:移位密码
(1)密文概率
(2)明文概率
三. 举例:多字母的移位密码
四. 完美安全
五. 举例:双子母的移位密码
六. 从密文角度看完美安全
七. 完美保密性质 一. 介绍…
CS188 Project 4: Inference in Bayes Nets(4-6)
CS188 Project 4: Inference in Bayes NetsQuestion 4 (4 points): Eliminate原理方法代码结果Question 5 (4 points): Normalize原理方法代码结果Question 6 (4 points): Variable Elimination原理方法代码结果数据及效果对比EliminateNormalizeVariable Elimination收获Quest…
线性递推关系的求解方法
线性递推关系的求解方法定义常系数线性齐次递推关系的求解定义定理例题:Fibonacci数常系数线性非齐次递推关系的求解定理特解表例题定义
设kkk是给定的正整数,若数列f(0),f(1),…,f(n),…f(0),f(1),\ldots,f(n),\ldotsf(0),f(1),…,f(n),…的相邻k1k1k1…
标准差有两种常见的估计方法:有偏估计和无偏估计
当我们谈论标准差时,有两种常见的估计方法:有偏估计和无偏估计。 有偏估计(Biased Estimate):有偏估计是指使用样本标准差来估计总体标准差,而不应用修正因子。这种估计方法在某些情况下可能导致总体标准差…
史诗级长文--朴素贝叶斯
引言 朴素贝叶斯算法是有监督的学习算法,解决的是分类问题,如客户是否流失、是否值得投资、信用等级评定等多分类问题。该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。但由于该算法以自变量之间的独立&am…
【线性代数与矩阵论】范数理论
范数理论
2023年11月16日 文章目录 范数理论1. 向量的范数2. 常用向量范数3. 向量范数的等价性4. 矩阵的范数5. 常用的矩阵范数6. 矩阵范数与向量范数的相容性7. 矩阵范数诱导的向量范数8. 由向量范数诱导的矩阵范数9. 矩阵范数的酉不变性10. 矩阵范数的等价性11. 长方阵的范数…
机器学习---无偏估计
1. 如何理解无偏估计
无偏估计:就是我认为所有样本出现的概率⼀样。 假如有N种样本我们认为所有样本出现概率都是
1/N。然后根据这个来计算数学期望。此时的数学期望就是我们平常讲 的平均值。数学期望本质就
是平均值。
2. 无偏估计为何叫做“无偏”࿱…
绘制X-Bar-S和X-Bar-R图,监测过程,计算CPK过程能力指数
X-Bar-S图和X-Bar-R图是统计质量控制中常用的两种控制图,用于监测过程的稳定性和一致性。它们的主要区别在于如何计算和呈现数据的变化以及所关注的问题类型。 X-Bar-S图(平均值与标准偏差图): X-Bar代表样本均值,S代表…
rand5()得到rand3()或rand7()类型题:通过rand n()实现rand m()
文章目录rand5()得到rand3()rand5()得到rand7()通过rand n()实现rand m()rand5()得到rand3()
通过rand5实现rand3很好实现,rand5的取值为[1,2,3,4,5]的值,但是rand3的取值[1,2,3],由此可得,当rand5随机到4,5时可以重新…
SPSS多元对应分析
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件请点击此链接下…
【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布(3,二维随机变量函数的分布)
文章目录 七、二维随机变量函数的分布7.1 二维随机变量函数分布的基本情形 ( X , Y ) (X,Y) (X,Y) 为二维离散型随机变量 ( X , Y ) (X,Y) (X,Y) 为二维连续型随机变量 X X X 为离散型变量, Y Y Y 为连续型变量 7.2 常见二维随机变量的函数及其分布 Z min { X ,…
【浓缩概率】浓缩概率思想帮我蒙选择题的概率大大提升!
今天在学习的时候遇到一个很有趣的思想叫作浓缩概率,可以帮我们快速解决一下概率悖论问题!
什么是概率
计算概率有下面两个最简单的原则:
原则一、计算概率一定要有一个参照系,称作「样本空间」,即随机事件可能出现…
四磺化酞菁镓(GaTSPc),酞菁有机半导体材料,齐岳生物提供酞菁定制产品
四磺化酞菁镓(GaTSPc),酞菁有机半导体材料,齐岳生物提供酞菁定制产品
磺化酞菁鲸具有较强的荧光,作为生物体中癌细胞检测和抑制其生长的活性物质的研究正日益引起人们的兴趣]。但磺化酞菁鲸在水溶液中有较强的二聚作用,二聚体激发态的快速内…
拒绝拖延,从我做起!
拒绝拖延,从我做起!
如果有一件事,对你的未来很重要,千万不要说等以后再做,这是无限拖延的借口【等有时间再做】的真正含义是,闲得无聊再去做,意味着事情即不重要也不紧急该做的重要事情不做&a…
【小呆的概率论学习笔记】抽样调查之用抽样样本估计母体数字特征
文章目录 1. 随机变量的数字特征1.1 随机变量的均值(期望)1.2 随机变量的方差1.3 随机变量的协方差 2. 抽样调查3. 用抽样样本估计母体数字特征3.1 估计母体样本均值3.2 抽样样本均值的方差3.2 估计母体样本方差 1. 随机变量的数字特征
随机变量本质上是…
【概率论笔记】正态分布专题
文章目录一维正态分布多维正态分布n维正态分布二维正态分布一维正态分布
设X~N(μ,σ2)X\text{\large\textasciitilde}N(\mu,\sigma^2)X~N(μ,σ2),则XXX的概率密度为f(x)12πσe−(x−μ)22σ2f(x)\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}f(…
算法模板(5):数学(1):数学知识(2)combination
排列组合是组合数学中的基础。排列就是指从给定个数的元素中取出指定个数的元素进行排序;组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。排列组合与古典概率论关系…
【机器学习前置知识】Beta分布
Beta分布与二项分布的关系
Beta分布与二项分布密切相关,由二项分布扩展而来,它是用来描述一个连续型随机变量出现的概率的概率密度分布,表示为 X X X~ B e t a ( a , b ) Beta(a,b) Beta(a,b) , a 、 b a、b a、b 是形状参数。Beta分布本质上也是一个概率密度函数,只是这…
看见统计——第三章 概率分布
看见统计——第三章 概率分布
参考
https://github.com/seeingtheory/Seeing-Theory中心极限定理
概率分布描述了随机变量取值的规律。
随机变量Random Variables
🔥 定义:将样本空间中的结果映射到实数的函数 XXX 称为随机变量(random variable)&a…
0基础学习diffusion_model扩散模型【易理解的公式推导】
0基础学习diffusion_model扩散模型【易理解的公式推导】一、概述二、扩散过程(已知X0求Xt)三、逆扩散过程(已知Xt求Xt-1)1。算法流程图四、结论五、损失函数六、心得体会(优缺点分析)一、概述 DDPM论文链接: Jonathan Ho_Denoising Diffusion…
概率论 1.3 古典概型与几何概型
1.3.1 排列与组合排列从n个不同元素任取r(r<n)个元素排成一列(考虑元素出现的先后次序),称此为一个排列,此种排列的总数为n(n-1)....(n-r1)n!/(n-r)!,若rn,则称为全排列,2.重复排列从n个不同元素中每次取出一个,放回…
随机过程 基本概念和基本类型
文章目录随机过程 基本概念和基本类型基本概念有限维分布和 Kolmogorov 定理基本类型平稳过程平稳过程的定义平稳过程的遍历性独立增量过程随机过程 基本概念和基本类型
基本概念
随机过程 :定义为概率空间 (Ω,F,P)(\Omega,\,F,\,P)(Ω,F,P) 上的一族随机变量 {X…
8.2 正态总体的参数的检验
学习目标:
如果我要学习正态总数的参数检验,我会按照以下步骤进行学习: 学习正态分布的基本知识:正态分布是统计学中非常重要的概率分布之一,掌握其基本知识包括概率密度函数、期望值、方差、标准差等是非常重要的。 …
8.3 总体分布的假设检验
学习目标:
如果我要学习总体分布的假设检验,我会采取以下步骤: 掌握基础概念:学习和掌握统计学中基础的概念,如总体、样本、假设检验、p值等等。 学习检验方法:了解和学习不同的总体分布假设检验方法&…
TJOI 2015 概率论 题解
TJOI 2015 概率论 题解 题意 求 \(n\) 个点随机生成的有根二叉树(所有互不同构的二叉树出现情况等概率)的叶子节点数的期望值。 题解 70 答案显然是 \(\dfrac{g(n)}{f(n)}\) ,\(g(n)\) 是 \(n\) 个点为所有二叉树的叶子总数, \(f(n)\) 是 \(n\) 个点能生…
数据处理:归一化与标准化
归一化与标准化 归一化和标准化是数据预处理时常用的方法,它们都可以将数据映射到特定的区间内,但是具体的实现方式和应用场景有所不同。 1 归一化与标准化的相同点
都能够处理特征值之间的差异性,避免特征值之间的度量不一致或者差异过大都…
随机过程 Markov 链(中)
文章目录 随机过程 Markov 链(中)极限定理及平稳分布极限定理平稳分布与极限分布 随机过程 Markov 链(中)
极限定理及平稳分布
极限定理
Th:(基本极限定理)若状态 i i i 是周期为 d d d 的…
Nested Logit交通方式划分-基于Biogeme
前段时间做交通模型,需要用到nested-logit模型做交通方式划分,常用的工具有SPSS、TransCAD,近期发现一个开源的软件Biogeme,尝试着做了一下。 1.原理部分可参考概率论书籍和关宏志教授的《非集计模型交通行为分析的工具》…
数理统计基础:参数估计与假设检验
在学习机器学习的过程中,我充分感受到概率与统计知识的重要性,熟悉相关概念思想对理解各种人工智能算法非常有意义,从而做到知其所以然。因此打算写这篇笔记,先好好梳理一下参数估计与假设检验的相关内容。 1 总体梳理
先从整体结…
Sub-Gaussian随机变量
文章目录引言Sub-Gaussian等价的几个性质Sub-Gaussian随机变量的定义Sub-Gaussian随机变量的三个例子Sub-Gaussian的近似旋转不变性总结引言
Sub-Gaussian的分布跟标准高斯分布N(0,1)\mathcal N (0,1)N(0,1)的性质密切相关,因此在介绍Sub-Gaussian随机变量之前&…
概率图模型--最大后验概率状态推理MAP
概率图模型–最大后验概率状态推理MAP – 潘登同学的Machine Learning笔记 文章目录概率图模型--最大后验概率状态推理MAP -- 潘登同学的Machine Learning笔记简单回顾概率图模型的推理最大后验概率状态推理MAP变量消元法求与团树传播算法求MAP举个栗子(以三个变量为例)MRF应用…
贝叶斯公式与全概率公式的理解。
1.贝叶斯与全概率公式解释
1.全概率公式定义 即若在某个场景下,可找到一个完备事件组 Ai ( i 1,2,3…n)。 则对任一与该场景有关的事件 B,都可以分割成无数个小事件(由不同因素引起的事件) 有: B B ∩ A1 ∪ A2…
概率 | 【提神醒脑】重难点专题突破 自用笔记
本文总结参考于 kira 2023概率提神醒脑技巧班 中 —— 重难点专题。 笔记均为自用整理。加油!ヾ(◍∇◍)ノ゙ 一研为定! 一、条件均匀 / 指数 / 二项…分布 -------------------------------------------------------------------------------------------------------------…
Generalized-ICP(GICP)論文研讀
Generalized-ICP論文研讀前言損失函數推導應用point-to-pointpoint-to-planeplane-to-plane前言
ICP最基本的形式是point-to-point,即以點到點之間的距離作為損失函數;它的一個變種是point-to-plane,改用點到目標點局部擬合平面的距離作為損…
兩獨立高斯隨機變數之和
兩獨立高斯隨機變數之和XY∼N(μXμY,σX2σY2)XY \sim \mathcal{N}(\mu_X \mu_Y, \sigma_X^2 \sigma_Y^2)XY∼N(μXμY,σX2σY2)
以下證明參考Sum of normally distributed random variables - Proof using characteristic functions。
兩個隨機變數X,YX,YX,Y的特…
【概率论】期末复习笔记:数理统计学的基本概念
数理统计学的基本概念目录一、总体与样本二、样本数据的整理1. 样本频数分布与频率分布2. 频率直方图3. 经验分布函数三、统计量1. 统计量的概念2. 几个常用的统计量1) 样本均值2) 样本方差和样本标准差3) 样本矩4) 顺序统计量5) 样本极差6) 样本ppp分位数四、抽样分布1. Γ\Ga…
【概率论】期末复习笔记:参数估计
参数估计目录一、点估计1. 估计量的概念2. 估计量的求法矩估计法最大似然估计法二、估计量的评选标准1. 无偏性2. 有效性3. 相合性总结三、区间估计1. 双侧区间估计2. 单侧区间估计四、正态总体参数的区间估计σ2\sigma^2σ2已知,考察μ\muμ</font>σ2\sigma…
小实验:关于期望的乘法性质
小实验:关于期望的乘法性质 引言个人疑惑验证过程样本生成实验过程 附:完整代码 引言
本节通过代码实现期望的乘法性质。
个人疑惑
在数学期望的定义中,有一条随机变量期望的乘法性质: 当随机变量 X , Y \mathcal X,\mathcal Y…
机器学习笔记之深度信念网络(二)模型构建思想(RBM叠加结构)
机器学习笔记之深度信念网络——模型构建思想引言回顾:深度信念网络的结构表示解析RBM隐变量的先验概率通过模型学习隐变量的先验概率引言
上一节介绍了深度信念网络的模型表示,本节将介绍深度信念网络的模型构建思想——受限玻尔兹曼机叠加结构的基本逻…
神经网络基础部件-BN层详解
一,数学基础
1.1,概率密度函数
随机变量(random variable)是可以随机地取不同值的变量。随机变量可以是离散的或者连续的。简单起见,本文用大写字母 XXX 表示随机变量,小写字母 xxx 表示随机变量能够取到…
概率论:数理统计基本概念——总体与样本
总体与个体: 总结: 多维的怎么办?: 直方图和经验分布函数: 可以看到上面的这个其实就相当于密度分布函数。那分布函数怎么办?:
RANSAC算法理解
RANSAC是“RANdom SAmple Consensus(随机抽样一致)”的缩写。它可以从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果;为了提高概率必须提高迭代次…
概率论:条件概率与独立性
定义: 若AB独立,那么AB,AB,AB就都独立了。有一个不独立,那其他的就都不独立。
简单证明: 来个小例题,主要学标准写法: 有限多个事件的独立性: 注意:4个条件都要满足才叫ABC相互独立…
显著性检验【t-test、方差分析、ks检验】
显著性检验【t-test、方差分析、ks检验】
0、目录
1显著性检验基本定义(what?)
2.使用显著性检验的意义(why? )
3.显著性检验的具体操作流程(how? )
1、显著性检验基本定义
统计假设检验…
概率论2:随机事件与概率
概率定义:
古典概率模型:样本空间有限,基本事件等可能。 几何概型: 统计概率:
先对频率做定义: 那么概率的统计学定义是什么?: 概率的公理化定义: 看起来很复杂的样子 …
看骰子的六个面需要多少次
看骰子的六个面需要多少次 – 潘登同学的概率论笔记
来源
前几天在刷视频的时候,发现了这样一道题 解答
简化为硬币问题
一般做法
假设两次就能看到硬币的正反面,那么出现的情况可能为"正反"or“反正”(另外两个为"正正"&#…
什么是Dirichlet分布?
Dirichlet分布是一种概率分布,用于描述多维随机变量的概率分布。它是一个连续分布,通常用于处理具有多种可能取值的离散型随机变量。在LDA模型中,Dirichlet分布通常被用作先验分布,用来表示主题的概率分布和单词的概率分布。
Dir…
2.2 离散型随机变量
引入:有些随机变量,它全部可能取到的值是有限个或可列无限多个,这种随机变量称为离散型随机变量:例如,掷骰子朝上一面的点致,一唇夜 110 接到的呼叫次数等均为离散型随机变量.2.2.1 离散型随机变量的分布律定义2.3 设X是一个离散型随机变量&a…
刷题记录:P8804 [蓝桥杯 2022 国 B] 故障 条件概率
传送门:洛谷
题目描述:
题目较长,此处省略
输入:
3 5
30 20 50
0 50 33 25 0
30 0 35 0 0
0 0 0 25 60
1
3
输出:
2 56.89
1 43.11
3 0.00读完题目,我们会发现其实题目给了我们两个事件,并且这两个事件是相互关联的.因此不难想到使用条件概率
我们将故障原因看做事件AAA,结合…
【数项级数】无穷个数相加一定是个数吗?
数项级数 引入思考问题转化 定义总结重要的例子练习题 引入
思考
数项级数,其实就是要解决无穷个数相加的问题。 而对于无穷求和的问题,思考:无穷个数相加一定是个数吗? 下面,我们来举几个例子: 1 2 2 …
量化投资 离散时间随机过程
文章目录 量化投资 离散时间随机过程状态空间 State Space状态域和事件域概率测度 随机变量 Random Variable分布 CDF and PDF期望和条件期望 Expectation and conditional expectation独立性 Independence特征方程 Characteristic Functions范数空间 Norm Space收敛性 Converg…
一文懂KL散度KL Divergence
本文翻译自https://naokishibuya.medium.com/demystifying-kl-divergence-7ebe4317ee68 KL散度中的KL全称是Kullback-Leibler,分别表示Solomon Kullback和Richard A.Leibler这两个人。
一、KL散度的定义 KL散度表明概率分布Q和概率分布P之间的相似性,由…
统计学_贾俊平——思考题第 10 章 方差分析
1.什么是方差分析?它研究的是什么? 答:方差分析就是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。 表面上看,方差分析是检验多个总体均值是否相等的统计方法,但本质上它所…
【分布族谱】均匀分布和三角形分布的关系
文章目录 均匀分布和三角分布均匀分布相加对数均匀分布 均匀分布和三角分布
均匀分布是最容易理解的连续随机分布,实际上就是等概率的连续分布,其PDF为 f ( x ) 1 b − a , x ∈ ( a , b ) f(x)\frac{1}{b-a}, x\in (a,b) f(x)b−a1,x∈(a,b)
其样本…
机器学习-5 朴素贝叶斯算法
朴素贝叶斯算法 算法概述数理统计学处理的信息古典学派和贝叶斯学派的争论贝叶斯定理朴素贝叶斯分类训练朴素贝叶斯:朴素假设案例:预测打网球拉普拉斯平滑技术小结 算法流程与步骤算法应用sklearn中的朴素贝叶斯朴素贝叶斯的使用算法实例 算法概述
数理…
【计量经济学】联立方程模型
联立方程模型 – 潘登同学的计量经济学笔记 文章目录联立方程模型 -- 潘登同学的计量经济学笔记联立方程模型(SEM)一个合适的列子一个不合适的例子联立性偏误结构方程的识别与估计已婚工作妇女的劳动供给通货膨胀与开放度多于两个方程的系统时间序列的联立方程模型对持久性收入…
【计量经济学】跨时期横截面的混合
跨时期横截面的混合–潘登同学的计量经济学笔记 文章目录跨时期横截面的混合--潘登同学的计量经济学笔记独立横截面的混合例子1:不同时期的妇女生育率例子2: 教育回报和工资中性别差异的变化跨时结构性变化的邹至庄检验政策分析的一般做法两时期面板数据分析失业率与…
信息量、熵、联合熵、条件熵、相对熵、交叉熵、JS散度、Wasserstein距离
信息量 I ( x i ) l o g 1 P ( x i ) − l o g P ( x i ) I(x_i)log \frac {1}{P(x_i)}-logP(x_i) I(xi)logP(xi)1−logP(xi) 信息量(self-information),又译为信息本体,由克劳德 香农(Claude Shannon&…
联合分布,边缘分布,条件分布,互信息
注意:分布和概率有时候会混乱,有时候P(X)表示X的分布,有时候用F(X),有时候用p(X),具体的直接看作者说它是啥就是啥吧
分布函数
要求F(X)F(X)F(X),实际上是FX(x)P{X<x}F_X(x)P\{X<x\}FX(x)P{X<…
熵,交叉熵,KL散度,条件熵
参考理解熵与交叉熵 - 九号的文章 - 知乎 https://zhuanlan.zhihu.com/p/389293738 熵
计算公式:H(a)−log(p(a))H(a) -log(p(a))H(a)−log(p(a)) 就是信息量,对于一个事件A,的一种情况的信息量,由情况a_i发生的概率决定 举个例…
概率图模型--HMM
概率图模型–HMM – 潘登同学的Machine Learning笔记 文章目录概率图模型--HMM -- 潘登同学的Machine Learning笔记马尔可夫链HMM基本假设HMM 的两个空间和三组参数HMM的三个基本问题概率计算问题(evaluation问题)预测问题(解码问题)学习问题马尔可夫链
有向图模型(…
【计量经济学】时间序列回归中序列相关
【计量经济学】时间序列回归中序列相关 --潘登同学的计量经济学笔记 文章目录【计量经济学】时间序列回归中序列相关 --潘登同学的计量经济学笔记自相关含义产生原因自相关的后果含序列相关误差时OLS的性质无偏性和有效性有效性和推断拟合优度纠正说法序列相关的检验回归元为严…
共轭先验分布及其应用
共轭先验分布及其应用 – 潘登同学的数理统计笔记 文章目录共轭先验分布及其应用 -- 潘登同学的数理统计笔记共轭先验分布正态分布的共轭先验分布为正态分布其他的常用的共轭先验分布为什么要有共轭先验分布这一概念共轭先验分布
设总体ξ\xiξ的分布函数为F(x;μ,σ)F(x;\mu,…
vue组件传值、通信
vue组件传值、通信 父组件--------》子组件 属性 // parent
<HelloWorld msg"Welcome to Your Vue.js App"/>// child
props: { msg: String } 引用refs // parent
<HelloWorld ref"hw"/>修改子组件的值
this.$refs.hw.xx xxx 子组件chidren …
【计量经济学】统计推断
统计推断 --潘登同学的计量经济学笔记 文章目录统计推断 --潘登同学的计量经济学笔记单个总体参数的检验t检验p值法置信区间法多个线性约束的检验F检验F检验的R2R^2R2调整R2R^2R2p值法回归整体显著大样本检验联合检验LM统计量单个总体参数的检验
t检验
检验步骤
原假设H0:β…
【计量经济学】模型设定问题
模型设定问题–潘登同学的计量经济学笔记 文章目录模型设定问题--潘登同学的计量经济学笔记函数误设问题RESET -- 对函数误设的检验RESET的作用及缺陷对非嵌套模型的检验构造综合模型戴维斯-麦金农检验(Davidson and MacKinnon[1981])非嵌套模型检验的问题代理变量找到代理变量…
武忠祥老师每日一题||定积分基础训练(二)
仍是上一节中提到的基本思想 武忠祥老师每日一题||定积分基础训练(一) 在这个题中,M和N可以利用奇偶性判断。 如下: 从上可知, M ∫ − π 2 π 2 1 d x M\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}1\,{\rm d}x M∫−…
机器学习之朴素贝叶斯一
一、概述
朴素贝叶斯算法是典型的有监督学习算法,解决的是分类问题 贝叶斯算法是一种基于贝叶斯定理的分类算法,它的优点和缺点如下:
优点:
算法原理简单易懂,实现较为容易;可以利用先验知识对模型进行训…
每天一道算法练习题--Day25 第一章 --算法专题 --- ----------蓄水池抽样
蓄水池抽样 问题描述算法描述相关题目总结 力扣中关于蓄水池抽样问题官方标签是 2 道,根据我的做题情况来看,可能有三四道。比重算是比较低的,大家可以根据自己的实际情况选择性掌握。
蓄水池抽样的算法思维很巧妙,代码简单且容易…
【计量经济学】异方差性
异方差性–潘登同学的计量经济学笔记 文章目录异方差性--潘登同学的计量经济学笔记异方差对OLS造成的影响异方差--稳健推断一个有效估计量多元回归的一个有效估计量异方差--稳健标准误的适用情况异方差--稳健的F统计量异方差--稳健的LM统计量一般的LM稳健的LM检验异方差性布罗施…
概率统计Python计算:一元线性回归应用——预测
对一元线性回归模型,若算得参数aaa,bbb和σ2\sigma^2σ2的估计量a∧\stackrel{\wedge}{a}a∧,b∧\stackrel{\wedge}{b}b∧和σ2∧\stackrel{\wedge}{\sigma^2}σ2∧。设xx0xx_0xx0为一指定值,依E(Y0)ax0bE(Y_0)ax_0bE(Y0)ax…
概率统计Python计算:一元线性回归未知参数的区间估计
在博文《一元线性回归未知参数的点估计》中利用scipy.stats的linregress函数,计算了总体分布N(axb,σ2)N(axb, \sigma^2)N(axb,σ2)的未知参数aaa,bbb和σ2\sigma^2σ2的无偏估计a∧\stackrel{\wedge}{a}a∧,b∧\stackrel{\wedge}{b}b∧和σ…
Kalman滤波(Part-1:信号模型基础)
Kalman Filters
Dynamical Signal Models
一阶高斯-马尔可夫过程(first-order Gauss-Markov process):描述采样点之间(相邻)的相关性: s[n]as[n−1]u[n](1)s[n] as[n-1] u[n] \tag{1} s[n]as[n−1]u[n](1)
其中u[n]u[n]u[n]是高斯白噪声…
概率统计Python计算:双正态总体已知总体方差总体均值差双侧假设的Z检验
设XXX和YYY相互独立且XXX~N(μ1,σ12)N(\mu_1,\sigma_1^2)N(μ1,σ12),YYY~N(μ2,σ22)N(\mu_2,\sigma_2^2)N(μ2,σ22),其中σ12\sigma_1^2σ12和σ22\sigma_2^2σ22是已知的。来自XXX和YYY的容量分别为n1n_1n1和n2n_2n2的样本均值为X‾…
概率统计Python计算:单个正态总体方差单侧假设的卡方检验
对正态总体的方差σ2≤σ02\sigma^2\leq\sigma_0^2σ2≤σ02(或σ2≥σ02\sigma^2\geq\sigma_0^2σ2≥σ02)进行显著水平α\alphaα下的假设检验,检验统计量n−1σ02S2\frac{n-1}{\sigma_0^2}S^2σ02n−1S2~χ2(n−1)\chi^2(n-1)χ2(…
【计量经济学】多元回归分析
多元回归分析–潘登同学的计量经济学笔记 文章目录多元回归分析--潘登同学的计量经济学笔记多元线性回归模型普通最小二乘法得到OLS估计值对OLS回归方程的解释多元线性回归中"保持其他因素不变”的含义OLS的拟合值和残差的性质(由单变量推广)对多元…
VAMP由浅入深(Part-3:状态演进分析数学基础(续))
文章目录考虑一般的收敛结论对定理4的证明证明方法对初始条件的确认数学归纳的推导这部分的小结考虑一般的收敛结论
对任意维度 NNN,给定一个正交阵V∈RNN\boldsymbol V \in \mathbb R^{N \times N}V∈RNN,以及一个初始向量u0∈RN\boldsymbol u_0 \in \…
AMP的推导和理解(Part-1)
文章目录前言问题模型硬约束下的压缩感知信号恢复(BP)软约束下的压缩感知信号恢复(LASSO)参数描述推导AMP的步骤BP问题下AMP的推导(AMP.0)(1)因子图与消息传递(2)大系统极限下的近似(3ÿ…
概率统计Python计算:离散型自定义分布数学期望的计算(二)
对于联合分布律为 的2-维离散型随机向量(X,Y)(X,Y)(X,Y),其函数g(X,Y)g(X,Y)g(X,Y)的数学期望E(g(X,Y))∑i1m∑j1ng(xi,yj)pijE(g(X,Y))\sum\limits_{i1}^m\sum\limits_{j1}^ng(x_i,y_j)p_{ij}E(g(X,Y))i1∑mj1∑ng(xi,yj)pij是2-维数组(g(x1,y1)g(x1,y2…
概率密度函数及其在信号方面的简单理解(中)频谱密度函数
概率密度函数及其在信号方面的简单理解(中)频谱密度函数
(中)频谱密度函数傅里叶级数傅里叶变换参考文献后记 上学期修了外学院的自动控制原理课,学习非线性控制系统的处理时用到了傅里叶级数,老师就让我…
概率统计Python计算:离散型随机向量条件分布计算
计算2-维离散型随机向量(X,Y)(X,Y)(X,Y)的条件分布律,譬如P(X∣Yyj)P(X|Yy_j)P(X∣Yyj),就是用YYY的边缘分布中的P(Yyj)p⋅jP(Yy_j)p_{\cdot j}P(Yyj)p⋅j遍除联合分布律中第jjj列中每个元素pijp_{ij}pij,i1,2,⋯ni1, 2, \cdots ni1,…
概率统计Python计算:离散型2-维随机向量的联合分布律及边缘分布
此处,我们假定2-维离散型随机向量(X,Y)(X, Y)(X,Y)的联合分布律为 即随机变量XXX取mmm个值,YYY取nnn个值,将(X,Y)(X, Y)(X,Y)的联合分布中的概率值构成一个mnm\times nmn的矩阵,记为PXYP_{XY}PXY,即 PXY(p11p12⋯p1…
概率论:参数估计——区间估计
点估计是有局限性的: 由此,我们就要推出我们的区间估计了: 就是说,参数范围小的时候精度高,但是落在这个范围以内的概率小,于是可行度降低; 这个概率指的是真值在这个区间里的概率。 记得物理实…
数字逻辑:同步时序逻辑
先学习状态机: 两种状态机: 可以看到两种状态机的区别,Mealy次态是由现态和输入决定的,输出也是如此;Moore则只输出现态。通过流程图看到,二者的区别只是在输出一步有没有考虑input的区别而已,现…
近世代数:置换群、陪集指数和Lagrange定理
置换群,顾名思义,就是置换组成的群,这个置换就是双射变换的意思,因此大家都是对称群的子群。大家老换来换去的也不分谁是谁了,干脆就1234表示吧。K-循环就是大家像跑火车一样跑一圈。 无公共数码的意思是两个轮换&…
概率统计Python计算:连续型随机变量分布(uniform expon)
1. uniform分布(均匀分布)
Python的scipy.stats包中的对象uniform表示连续型的均匀分布。下表展示了uniform分布的几个常用函数。
函数名参数功能rvs(loc, scale, size)loc:分布参数aaa,缺省值为0, scale:…
概率统计Python计算:离散型随机变量分布(binom poisson)
1. binom分布(二项分布)
scipy.stats包中的binom类对象是表示二项分布的。常用的四个函数说明见下表。
函数名参数功能rvs(n, p, size)n,p:分布参数,size:产生的随机数个数,缺省值为1产生size…
概率统计Python计算:离散型随机变量分布(bernoulli geom)
Python的scipy.stats包中提供了各种随机变量的分布。每一种分布,其累积分布函数(分布函数)记为cdf。离散型变量分布的概率质量函数(分布律),记为pmf。除此之外,每个分布都有一个服从该分部变量发…
逻辑代数:逻辑运算与定理,代数化简
公理: 基本定理: 交换律,结合律自不必说,分配律你见过吗?: 好像把与变成或,或变成与对等式不影响?没错,这叫对偶式: 注意不要改优先级。可以用括号。 还有更多…
概率论与数理统计(3.4) 相互独立的随机变量
文章目录一、随机变量的相互独立性说明:例题例1例2例3二、推广到n维随机变量实际这一部分也是粗略的对所学几个重要概念的一个总结与推广。分布函数概率密度函数边缘分布函数边缘概率密度函数相互独立性结论一、随机变量的相互独立性 说明:
二维离散型随…
概率论与数理统计(3.3)二维随机变量条件分布
这个条件分布主要只针对二维的
一、离散型随机变量的条件分布 同理固定一个X为一个常数则可得Y的条件分布律 **注:**离散型的求在什么条件下X或Y的条件分布律,知道他们的联合分布律很重要. 1) 观察这个公式。 注:必须知道P{X1}的…
概率论与数理统计(3.2)边缘分布
边缘分布一、边缘分布函数二、离散型随机变量边缘分布律三、连续型随机变量的边缘分布四、二维均匀分布五、二维正态分布一、边缘分布函数
定义: 联合分布函数和边缘分布函数的关系:
二、离散型随机变量边缘分布律 实质就是固定一个随机变量而对另外…
2023年计算机考研英语一作文模板|考研要不要使用英语模板?
2023年计算机考研英语考英语一,计算机考研基本是考计算机科学与技术这个大类,属于学硕,考研英语一是全国统一的。那么2023年计算机考研英语一作文怎么写呢?要不要参考模板呢?
首先请看下2023年计算机考研英语一作文模板:建议信…
近世代数1:映射,变换
映射的定义: 分类:单,满,双。 定理一: 映射判断相等: 变换:到自身的变换。
任意n元集有n!个双射变换。
基于logistics回归的评分卡模型【相关理论】
评分卡模型KS和roc曲线KS值ROC 曲线AUC评分卡 分箱 WOE IV分箱WOE与IV值逻辑回归模型转化为评分卡:KS和roc曲线 TN:将负类预测为负类(真负类)FN:将正类预测为负类(假负类)TP:将正类预…
UOJ #593. 新年的军队 题解
#593. 新年的军队
属实是一道神仙题,估计是去年这个时候听说了这道题,最近把这个坑填了。
给后面要来写的人提个醒,这个题其实没有想象地那么恐怖,代码其实也不复杂,只是推导十分困难。
我说我这篇是全网最详细的不…
概率论与数理统计之随机试验与随机时间样本空间与事件的集合表示
引言
确定性(必然):一定发生(不发生)随机(偶然):可能发生,可能不发生统计规律:对事情做大量的重复的试验试图找出某种规律
1.1.1 随机试验和随机事件
试验:观察、测量、…
机器学习 复习笔记(3) 回归
根据y值,分成回归与分类。y是连续值就是回归问题,y是离散值就是分类问题。 x是样本,θ是参数。θ是未知的,x是已知的。
Question:为什么我们预测出来的模型会和实际值有误差 ε? 因为根据已知特征和给定…
数学建模系列-评价模型(四)---主成分分析法
主成分分析法可以理解为层次分析法的一种衍生,是为了舍去无用或者效用较少的参数来达到拟合的目的,为了简化计算。
主成分与原始变量之间的关系: (1)主成分保留了原始变量绝大多数信息。
(2&#x…
【读书笔记->统计学】09-02 将正态分布运用到其他概率分布-用正态分布近似代替二项分布、泊松分布概念简介
用正态分布近似代替二项分布
假设一个情境:有40道题,每一道你都不知道答案,答对概率为1/4。求答对30题及以上的概率。
这个是典型的二项分布,具体介绍见:【读书笔记->统计学】07-02 离散型概率分布-二项分…
【读书笔记->统计学】09-01 将正态分布运用到其他概率分布-正态分布的相加、线性变换与独立观察结果概念简介
将正态分布运用到其他概率分布
正态分布的相加
假设一个情境:德克想到了“爱情过山车”的创意,让新婚夫妇在过山车上办婚礼。在这之前,需要确保他所设想的特别座驾能够承载新郎和新娘的重量。他设想的座驾最多承载380磅的重量,求…
随机森林(袋外OOB数据)
1.在数据抽样的时候,因为是有放回的采样,有很多条样本没有被选到,经过以下计算,
没条样本大概有百分之三十的概率是没有被采样的。 2.对于这些没有被采样到的数据(oob),我们希望能够得到利用当…
概率统计Python计算:经典分布数学期望的计算
我们知道Python的scipy.stats包提供了大量的经典分布(如0-1分布、二项分布、泊松分布,均匀分布,指数分布,正态分布……等等),这些经典分布对象拥有计算数学期望的expect函数,该函数常见分布的调…
概率统计Python计算:标准正态分布分位点计算
标准正态分布对给定显著水平的分位点。设XXX~N(0,1)N(0,1)N(0,1),显著水平为α\alphaα。为计算右侧分位点zαz_{\alpha}zα(见下图),使得 P(X≤zα)1−αP(X\leq z_\alpha)1-\alphaP(X≤zα)1−α 由标准正态分布密度函数φ…
概率统计Python计算:连续型2-维随机向量分布的概率计算
为计算连续型随机向量(X,Y)∈D(X, Y)\in D(X,Y)∈D的概率P((X,Y)∈D)P((X, Y)\in D)P((X,Y)∈D)要用到2-重积分:∬Df(x,y)dxdy\iint\limits_{D}f(x, y)dxdyD∬f(x,y)dxdy,其中f(x,y)f(x, y)f(x,y)为(X,Y)(X, Y)(X,Y)的联合密度函数。若DDD可表示为 D{(…
事件驱动的Tempotron算法
1. 时间驱动的Tempotron学习算法
公式
突触前神经元输入一个脉冲会产生一个PSP(突触后电位),神经元的膜电位为所有突触前神经元产生的PSP加权和 V(t)∑iwi∑tiK(t−ti)Vrest(1.1)V(t)\sum_i{w_i}\sum_{t_i}K(t-t_i)V_{rest} \tag{1.1}V(t)i…
将原本属于[min,max]的数据放缩到任意区间[a,b]
1. 找到原本数据的最大值max,最小值min
2. 计算放缩系数:k(b-a)/(max-min)
3. 原来数据x经过放缩得到y a k *(x-min)或者 y b k *(x-max)
参考链接&am…
(01)ORB-SLAM2源码无死角解析-(58) 闭环线程→计算Sim3: 源码Sim3Solver::iterate()讲解
讲解关于slam一系列文章汇总链接:史上最全slam从零开始,针对于本栏目讲解的(01)ORB-SLAM2源码无死角解析链接如下(本文内容来自计算机视觉life ORB-SLAM2 课程课件): (01)ORB-SLAM2源码无死角解析-(00)目录_最新无死角讲解:https://blog.csdn.net/weixin…
史上最简SLAM零基础解读(6) - 卡方分布(chi-square distribution)和()卡方检验(Chi-Squared Test) → 理论讲解与推导
本人讲解关于slam一系列文章汇总链接:史上最全slam从零开始 文末正下方中心提供了本人联系方式,点击本人照片即可显示WX→官方认证{\color{blue}{文末正下方中心}提供了本人 \color{red} 联系方式,\color{blue}点击本人照片即可显示WX→官方认证}文末正…
概率统计Python计算:自定义连续型分布
与rv_discrete类相仿,scipy.stats还提供了一个表示连续型分布的rv_continuous类。使用rv_continuos类自定义连续型分布甚至比用rv_discrete类自定义离散型分布更简单:只需要自定义分布的累积概率函数(分布函数)cdf即可。 例如&…
概率统计Python计算:自定义离散型分布
假定有自定义的分布数据(X, P),其中X表示随机变量XXX的取值序列,P表示对应XXX的每个取值的概率序列。scipy.stats包为我们提供了一个rv_discrete类,可以用数据(X, P)创建自定义的离散型随机变量的分布。例如设XXX~(12100.150.550.3)\begin{pm…
概率统计Python计算:离散型随机变量函数分布
设已知离散型随机变量XXX的分布律P(Xxk)pkP(Xx_k)p_kP(Xxk)pk,k1,2,⋯k1,2,\cdotsk1,2,⋯及函数Yg(X)Yg(X)Yg(X)为计算YYY的分布律,先算得序列{g(x1),g(x2),⋯}\{g(x_1), g(x_2), \cdots\}{g(x1),g(x2),⋯},对其中的每一个值g(xk)g(x…
概率统计Python计算:解2-维几何概型问题
对于2-维空间的几何概型,其中事件的概率须通过计算平面区域的面积才能求得。由函数曲线围成的区域D{(x,y)∣a≤x≤b,f1(x)≤y≤f2(x)}D\{(x, y)|a\leq x\leq b, f_1(x)\leq y\leq f_2(x)\}D{(x,y)∣a≤x≤b,f1(x)≤y≤f2(x)},其面积我们可以用二重积…
概率论与数理统计(4.3)协方差与相关系数基础知识总结
文章目录一、协方差1.定义2.与方差的关系3.性质4.计算公式定义计算公式计算二、相关系数1.定义2.定理3.意义4.不相关与相互独立一、协方差
1.定义
Cov(X,Y)为协方差。
2.与方差的关系 3.性质 4.计算公式
定义计算
离散型: 连续型:
公式计算 二、…
概率论与数理统计(2.3-2.4)随机变量的分布函数和密度函数(连续型)
一、2.3 随机变量的分布函数
1.定义 主要研究随机变量在某以区间内取值的概率情况。F(x)是x的一个普通实函数X是随机变量,x是参变量不同的随机变量可能会是相同的分布函数
2.性质 长利用性质2来求分布函数中的参数 3.重要公式
P{X<a} F(a)P{X>a} 1-P{x<…
概率论与数理统计(2.1-2.2)随机变量和离散型分布
一、 随机变量
1.定义
随机变量是一个函数,且是定义在样本空间上。即将S中的每个元素e与实数x对应起来。 随机变量的取值范围在试验之前就能确定,且随机变量跟随有不同概率出现的实验结果而取不同的值,因此随机变量的取值也具有一定概率规律…
Binary Cross Entropy
参考Understanding binary cross-entropy / log loss
一、Introduction
训练一个二元分类器( binary classifier)的时候,往往会用到binary cross-entropy / log loss作为损失函数。下面详细介绍这个损失函数binary cross-entropy
二、A Si…
数论_欧拉函数_快速幂_欧几里得_逆元_素数筛
数论的一些基本知识欧拉函数欧拉函数的基本概念欧拉函数的性质求欧拉函数值快速幂题目背景欧几里得算法(辗转相除法)求最大公因数扩展欧几里得算法算法描述代码实现扩展欧几里得算法的一些应用计算乘法逆元的代码素数筛欧拉函数
欧拉函数的基本概念
对…
一篇文章看透母函数、矩、矩母函数联系与区别
矩母函数的暴力拆解,看完即懂>>>一篇文章看透母函数、矩、矩母函数联系与区别导读Party1:母函数Party2:矩Party3:矩母函数一篇文章看透母函数、矩、矩母函数联系与区别
矩母函数?是《概率论》里面一个重要的定义,对统计学和当前AI底…
高斯判别分析(GDA)
高斯判别分析
建立高斯模型
【假设】:y∼Bernouli(Φ)y\sim Bernouli(\Phi)y∼Bernouli(Φ)x∣y0∼N(μ0,Σ)x|y0\sim N(\mu_0,\Sigma)x∣y0∼N(μ0,Σ)x∣y1∼N(μ1,Σ)x|y1\sim N(\mu_1,\Sigma)x∣y1∼N(μ1,Σ) 由贝叶斯公式可得: P(y∣x)p(x∣…
贝叶斯定理的三个视角
文章目录计算视角基本比率视角主观概率的修正计算视角
在计算层面,贝叶斯公式简化了条件概率的计算 P(A∣B)P(AB)P(B)P(B∣A)P(A)P(B)P(A|B) \frac{P(AB)}{P(B)} \frac{P(B|A)P(A)}{P(B)} P(A∣B)P(B)P(AB)P(B)P(B∣A)P(A)
基本比率视角
首先定义 A患病的人…
【概率论】独立性作业(二)
文章目录 填空题填空题 设 A₁,A₂,A₃相互独立,且P(A_{i})=2 \sqrt {3},i=1,2,3.试求A₁,A₂,A₃中 (1) 至少出现一个的概率=____ 【正确答案:26/27】; (2) 恰好出现一个的概率=____ 【正确答案:2/9】; (3) 最多出现一个的概率=____ 【正确答案:7/27】; 解: (1) 所求概率为 P…
先验概率和后验概率理解
先验概率和后验概率理解
对于统计学只是皮毛认识,在学校时根本不重视,如今机器学习几乎以统计学为基础发展起来的,头疼的紧,如今还得琢磨基础概念。
1、我自己的理解:
1)先验:统计历史上的经…
【题目记录】——2021中国大学生程序设计竞赛(CCPC)- 网络选拔赛(重赛)
文章目录1002 Kanade Doesnt Want to Learn CG 数学思维1004 Primality Test 思维 简单题1006 Nun Heh Heh Aaaaaaaaaaa 动态规划组合数题目集地址
2021中国大学生程序设计竞赛(CCPC)- 网络选拔赛(重赛)1002 Kanade Doesn’t Want…
印章(动态规划问题dp)
package com.seal;import java.util.Scanner;//共有n种图案的印章,每种图案的出现概率相同。小A买了m张印章,求小A集齐n种印章的概率。public class Main {/** 1.找到状态,由题目可知状态为两个,买了的印章个数i和集齐的印章的个数j;* 2.明确…
报童问题 (The Newsvendor Problem)
引言
本文介绍了一个经典的商品采购模型(报童问题)及其解法. 该模型通过考虑需求的不确定性来最大化销售利润. 注: 本文的主要内容参考Gallego1.
1. 报童问题
这是一个关于卖报商人采购报纸的问题. 每天早上, 卖报商以批发价0.3元(每份)向报社采购当天的报纸, 然后以零售价1…
终于搞清楚正态分布、指数分布到底是啥了!
↑ 点击上方 “可乐的数据分析之路” 关注 星标 ~ 大概率每天早8点25更新 哈喽,大家好,我是可乐今天这篇文章接2个月以前的那篇文章 离散型随机变量的概率分布,继续来聊聊连续型随机变量的概率分布,以及用Python如何实现。并非所…
《概率论与数理统计》第四版 浙江大学第1-5章复习
概率论的基本概念
统计规律性:在大量重复实验或观察中所呈现出的具有固定规律性随机现象: 自然界有确定性现象和随机现象,随机现象指个别实验中结果呈现不确定性,在大量重复实验中其结果又具有统计规律性,
概率论和数…
指数分布族与广义线性模型
文章目录指数分布族的定义自然参数形式1性质自然参数形式2性质可识别性巴苏定理广义线性模型总结指数分布族的定义
如果{Pθ:θ∈Θ}\{P_\theta: \theta\in\Theta\}{Pθ:θ∈Θ}是关于σ−\sigma-σ−有限测度ν\nuν定义在(Ω,F)(\Omega, \mathcal{F})(Ω,F)上的分布族&…
R语言中实现线性回归+l_0范数变量选择的包abess
文章目录模型理论函数介绍实例1:指定稀疏参数sss实例2:不指定稀疏参数sss实例3:根据边际最大效应进行预筛选模型理论
该包实现了一种多项式复杂度的算法来利用下面的模型进行最优子集选择: minβ∈Rp12n∥y−Xβ∥22,s.t.∥β∥…
关于贝叶斯网络的一些判定
贝叶斯网络在之前说到朴素贝叶斯的时候提到过,即类似下图就是一个简单的贝叶斯网络: 根据这个图我们可知联合概率
而根据这个式子以及我们观测的任一条件下每个事件发生的概率,我们就可以计算出任何概率。 通过贝叶斯网络判定条件独立
1.t…
R语言:时序图和自相关图
这学期的《应用时间序列分析》、《R语言》、《统计案例分析》都需要使用R语言,故将课程中学到的代码以及相关补充代码分享出来,一方面促进自身学习的积极主动性,另一方面或许可以给学习R语言的同学们提供一点点帮助。 rm(listls())
install.p…
精确率、召回率、准确率
1、精确率、召回率、准确率
TP:正类预测为正类 FN:正------>负 FP:负------>正 TN:负------>负
精确率:PTPTPFPP\frac{TP}{TPFP}PTPFPTP,表示预测为正的样本中有多少是真正的正样本࿱…
python计算中奖问题的概率
题目:抽奖中,宝箱中奖概率是20%,抽5个能不能保证100%中奖?
很显然,只要样本不是小于等于5个,那自然不能保证了
下面,我们用python来模拟一下这个抽奖的过程,这里用统计频率代替概率…
逻辑回归的损失函数(推导)
前言:
不管是逻辑回归还是线性回归,比较好的减少loss损失的方法就是GD梯度下降。
而用梯度下降就要用到求损失函数,求损失函数就要用到最大似然估计MLE。 1.逻辑回归的概率表达式 对于预测正确的概率,可以将上面两个式子合并 2.…
概率统计Python计算:假设检验应用——联列表中相互独立性的检验
设总体的所有个体可按两种不同的标志进行分类,常常希望通过随机抽样检验这两种标志是否相互独立。为解决此类问题,通常将取得的样本(X1,X2,⋯,Xn)(X_1,X_2,\cdots,X_n)(X1,X2,⋯,Xn)按第一种标志分成uuu个类,按第二种标志分成vvv个类&a…
酞菁绿,耐高温酞菁绿颜料, 酞菁有机颜料CAS: 1328-53-6
酞菁绿,耐高温酞菁绿颜料, 酞菁有机颜料CAS: 1328-53-6
化学类型: 酞菁类
别名: 酞菁有机颜料
CAS登记号: 1328-53-6
颜料索引号: C.I.颜料绿7(C.I.Pigment Green 7;P.G.7)
色光࿱…
likelihood和probability
虽然经常在paper和教程中看到“似然(likelihood)”的概念,但是一直都没有仔细研究似然与概率的区别,今天查了一些资料,有些收获,在此总结一下。
似然与概率的区别 简单来讲,似然与概率分别是针…
凸优化面试题:凸集 凸函数 凸优化
为什么研究凸优化先要从凸集的性质开始:
凸函数图像的上方区域,一定是凸集; 假如一个函数上方是凸集,这个函数就是凸函数
如何用向量表示几何体 什么是凸包 包含凸集的最小集合 如何计算一个凸集的 凸包是什么?时间复…
利用SVD求得两个对应点集合的旋转矩阵R和转移矩阵t的数学推导
1.问题描述
给定两个在d维空间中对应的点集合P{p1,p2,…,pn}P \{ p_1,p_2 ,\dots , p_n\}P{p1,p2,…,pn}和Q{q1,q2,…,qn}Q \{ q_1 ,q_2, \dots , q_n \}Q{q1,q2,…,qn},为了计算出它们之间的刚体变换,即 RRR 和ttt,可以将其建模为如下的…
SPSS两相关样本检验
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件请点击此链接下…
学习记忆——数学篇——案例——代数——均值不等式
文章目录 理解记忆法定义定义推导 重点记忆法用途记忆法使用前提做题应用及易错点两种用法 出题模式法模型识别 谐音记忆法一正二定三相等 秒杀方法 理解记忆法
定义
1.算术平均值:设有n个数 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn…
(熟记理解背诵推导)概率论与数理统计的基础知识1
以下列出的基本概念需要熟记。最好能够闭卷写出定义。
目录
一、概率论的基础概念
二、随机变量及其分布
三、多维随机变量及其分布
四、随机变量的数字特征
五、大数定律及中心极限定理
六、样本及抽样分布
七、参数估计
八、假设检验 一、概率论的基础概念
随机试验…
【概率论】全概率与贝叶斯公式作业
文章目录 选择题 选择题 已知事件A、B、C两两独立,且P(A)P(B)P(C)12,P(C|AB)1,则 P(AB|C)() A.1/4 B.1/2 C.1/3 D.1 【正确答案:B】 设A、B、C是随机事件,A与B互不相容,且P(AC) 1 2 \frac{1}{2} 21,P(B) 1 3 \frac{…
概率论(一)——最大似然估计
通俗易懂: https://www.zhihu.com/question/24124998 实际操作: https://www.matongxue.com/madocs/447.html
【问题思考总结】多维随机变量函数的分布的两种情况的计算方法【离连/连连】
问题
今天做李六第一套的时候发现,有的时候,面对这种第二问的题,很自然地就想到了Fz(z),然后进行化简,但是有的时候,像这道题,就突然发现P{XY<z}是一个非常复杂的形式…
第三章软件开发环境与工具的选用
一、学习内容
(一)软件工程过程
1. 定义:是为了获得软件产品或是为了完成软件工程项目需要完成的一系列软件工程活动;
2. ISO9000定义:是把输入转化为输出的一组彼此相关的资源和活动;
3. 四项基本活动…
机器学习之样本及统计量
在数理统计中,称研究对象的全体为总体,组成总体的每个基本单元叫个体。从总体X中随机抽取一部分个体 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN称 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN为取自X的容量为n的样本。 实际上,数理统计…
泊松分布 二项分布 正态分布 高斯分布 伯努利分布latex
注:此文章既可以用于了解泊松分布 二项分布 正态分布 高斯分布 伯努利分布,也可以用于练习latex 变量类型: 连续型变量 如:指数分布、正态分布 离散型变量 如:伯努利分布、二项分布、泊松分布 伯努利分布:…
【概率论】Python:实现求联合分布函数 | 求边缘分布函数 | Joint distribution | Marginal distribution
猛戳订阅! 👉 《一起玩蛇》🐍
💭 写在前面:本章我们将通过 Python 手动实现联合分布函数和边缘分布函数,部署的测试代码放到文后了,运行所需环境 python version >= 3.6,numpy >= 1.15,nltk >= 3.4,tqdm >= 4.24.0,scikit-learn >= 0.22。 0x00 …
第五章——大数定律和中心极限定理
文章目录1、大数定律1.1、弱大数定理(辛钦大数定理)1.2、伯努利大数定理2、中心极限定理2.1、独立同分布的中心极限定理2.2、李雅普诺夫定理2.3、棣莫弗——拉普拉斯定理2.4、中心极限定理的应用2.4.1、独立同分布的中心极限定理的应用2.4.2、棣莫弗——…
优思学院|如何利用六西格玛提升自己的大格局?
首先,我想说大格局并不仅仅是一个概念,更是一种生活态度。拥有大格局的人通常能够超越日常琐事,将目光投向更广阔的未来。他们不会被小事困扰,而是将注意力集中在更大的目标和使命上。拥有大格局的人常常具备卓越的领导力和判断力…
建立一个新的高阶数学教授模式,知其然,知其用,知其之所以然,知其所以然
1. 传统常用的模式 概念,性质,定理,定理证明,定理应用;
这个学习模式挺好的,但是定理证明过程往往很冗长,而且不易记忆,也就是说,即使推导了定理,初学者也记…
概率论1:随机事件与概率
随机实验是什么?: 即:重复进行,结果多样,不能确定。
用E代表随机实验。 样本空间: 只有一个样本点的叫基本事件。 必然事件: 用样本空间的名字代表必然事件。 注意:事件中的一个样…
概率论:随机变量之非离散变量
在讲非离散变量之前,先要讲讲分布函数: 相信你也发现了,这就是概率密度函数的积分。 分布函数有几条性质: 有了分布函数这个工具以后,我们就可以学习连续的随机变量了。 概率密度就是分布函数的微分。
概率密度的性质…
MineMine 算法(1)
这里写自定义目录标题 String smoothingOCR post process注意String smoothing
picked_tasks 来自dataframe
window_size = 5
window_strings = deque(maxlen=window_size)eliminated_result = []for idx, current_string in enumerate(picked_tasks):eliminated_result.appe…
概率论:随机变量及其分布
定义: 随机变量的特点: 随机变量可以分为离散的和非离散的,离散的可以一个一个列出来(可以无限),非离散无限且不可列。 离散随机变量: 分布列可以用图表,公式,画图展示。…
概率论:数字特征与极限定理——大数定律
极限定理是什么?: 就是在n趋近于无穷大的时候,Xn趋近于X。 大数定理: 注意x-u^2*f(x)就是方差的运算公式。这个只是不等式,用于单个变量,还不是大数定律。 意思是:有很多相互独立的变量X1X2X3&a…
线性代数——(期末突击)概率统计习题(概率的性质、全概率公式)
目录
概率的性质
题一
全概率公式
题二
题三 概率的性质
有限可加性:
若有限个事件互不相容,则 单调性:
互补性:
加法公式: 可分性: 题一 在某城市中共发行三种报纸:甲、乙、丙。在这个…
ADF 单位根检验 Dickey-Fuller 迪基-福勒检验
名词解释: Dickey-Fuller 迪基-福勒检验, 单位根检验, 如果存在时序数据中存在单位根, 则表明是非平稳序列 ADF检验 增广迪基-福勒检验 排除了自相关的影响
为什么需要检验: 单位根检验师时序序列分析的一个热点问题, 大部分时序模型都要求输入数据具有稳定性, 因此要先检测数…
【ChatGPT】一个凭借两百多年历史的公式崛起的巨星
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学本科在读,同时任汉硕云(广东)科技有限公司ABAP开发顾问。在学习工作中,我通常使用偏后端的开发语言A…
2025考研数学汤家凤高数、线代、概率论视频,百度网盘资源+PDF讲义
现在天气逐渐变凉,同学们都放寒假了!我个人觉得寒假是给有梦想的同学准备的!
我当时就喜欢放寒暑假,我觉得放假的时候别人在玩,我就能抽时间学习,来超越别人。所以好好利用寒假,绝对在考研的复…
Matlab如何计算功率谱熵?|信息熵之功率谱熵,完整代码及测试过程。
信息熵
熵的概念最初在热力学中提出,熵的本质被解释为即熵的本质是一个系统“内在的混乱程度”。熵的概念在不同的学科中引申出更为具体的概念,在信息论中信息熵的具体定义为: H ( X ) = p ( x i ) ∑ i = 1 n 1 p ( x
股票星期几买涨的概率大?
摘要:理论上讲星期几涨跌的概率一样大,但是实际上不是这样。于是我就写了几行代码,用统计学的方法来做了个统计分析。 每一周有五个交易日,哪天涨的概率会大一点?可能大家没考虑过这个问题,我之前买过一个股…
勘察设计考试公共基础之数学篇
1、数学
向量点积:向量叉积:平面的法向量为n(A,B,C),则该平面的点法式方程为:
A(x-x0)B(y-y0)C(z-z0)0
两平…
假设检验(三)(单侧假设检验)
在 《假设检验(二)(正态总体参数的假设检验)》中我们讨论了形如 H 0 : θ θ 0 ↔ H 1 : θ ≠ θ 0 H_0:\theta\theta_0 \leftrightarrow H_1:\theta \neq \theta_0 H0:θθ0↔H1:θθ0 的假设检验问题,其…
概率统计Python计算:假设检验应用——分布拟合检验
对来自总体XXX的样本X1,X2,⋯,XnX_1,X_2,\cdots,X_nX1,X2,⋯,Xn,及给定的显著水平α\alphaα检验假设H0:X的分布函数为F(x)(H1:X的分布函数不是F(x)).H_0:X\text{的分布函数为}F(x)(H_1:X\text{的分布函数不是}F(x)).H0:X的分布函数为F(x)(H1:X的分布函数…
概率统计Python计算:假设检验应用——基于成对数据的检验
设有nnn个相互独立的观测结果(X1,Y1)(X_1,Y_1)(X1,Y1),(X2,Y2)(X_2,Y_2)(X2,Y2),⋯\cdots⋯,(Xn,Yn)(X_n,Y_n)(Xn,Yn),诸对XiX_iXi和YiY_iYi受同一因素影响,DiXi−YiD_iX_i-Y_iDiXi−Yi~N(μ,σ…
概率统计Python计算:双正态总体方差比单侧假设的F检验
设总体XXX~N(μ1,σ12)N(\mu_1,\sigma_1^2)N(μ1,σ12),YYY~N(μ2,σ22)N(\mu_2, \sigma_2^2)N(μ2,σ22)相互独立,为检验右侧假设H0:σ12/σ22≤1,H1:σ12/σ22>1H_0:\sigma_1^2/\sigma_2^2\leq1,H_1:\sigma_1^2/\sigma_2^2>1H0:σ12…
概率统计Python计算:单个正态总体均值双侧假设的T检验
正态总体的方差σ2\sigma^2σ2未知的情况下,对总体均值μμ0\mu\mu_0μμ0进行显著水平α\alphaα下的双侧假设检验,检验统计量X‾−μ0S/n\frac{\overline{X}-\mu_0}{S/\sqrt{n}}S/nX−μ0~t(n−1)t(n-1)t(n−1)。其中X‾\overline{X}X和SSS分别…
概率统计Python计算:双正态总体方差比的双侧区间估计
计算两个正态总体方差比的区间估计涉及样本方差s12s_1^2s12,s22s_2^2s22,样本容量n1n_1n1,n2n_2n2和置信度1−α1-\alpha1−α等因素。双侧置信区间计算的具体算法如下
计算F(n1−1,n2−1)F(n_1-1,n_2-1)F(n1−1,n2−1)分布的以…
概率统计Python计算:单个正态总体方差的单侧区间估计
对函数sigma2Bounds(详见博文《单个正态总体方差的双侧区间估计》)稍作修改,就可得到计算总体参数σ2\sigma^2σ2单侧置信上限或下限的函数。
from scipy.stats import chi2 #导入chi2分布
def sigma2Bound(d, df, confi…
概率统计Python计算:用样本均值和方差计算总体参数的点估计
设来自总体XXX的简单样本为(X1,X2,⋯,Xn)(X_1, X_2,\cdots,X_n)(X1,X2,⋯,Xn)。样本均值为X‾1n∑i1nXi\overline{X}\frac{1}{n}\sum\limits_{i1}^nX_iXn1i1∑nXi,样本方差为S21n−1∑i1n(Xi−X‾)2S^2\frac{1}{n-1}\sum\limits_{i1}^n(X_i-\overline{X…
概率统计Python计算:协方差与相关系数计算
我们知道,若随机向量(X,Y)(X,Y)(X,Y)存在E(X)E(X)E(X),E(Y)E(Y)E(Y),E(XY)E(XY)E(XY),则存在(X,Y)(X,Y)(X,Y)的协方差Cov(Y,X)\text{Cov}(Y, X)Cov(Y,X): Cov(Y,X)E[(Y−E(Y))(X−E(X))]E(XY)−E(X)E(Y).\text{Cov}(Y,…
第四章 基于概率论的分类方法:朴素贝叶斯
文章目录 第四章 基于概率论的分类方法:朴素贝叶斯4.1基于贝叶斯理论的分类方法4.2条件概率4.3使用条件概率来分类4.5使用python进行文本分类4.5.1准备数据4.5.2训练算法4.5.3测试算法 第四章 基于概率论的分类方法:朴素贝叶斯
4.1基于贝叶斯理论的分类…
从极大既然估计的角度推导均方误差最小化
问题背景
曲线拟合问题,给定参数www和输入xxx,用多项式函数来拟合曲线,其中MMM表示多项式的次数: y(x,w)w0w1xw2x2...wMxMy(x,w) w_0 w_1xw_2x^2...w_Mx^M y(x,w)w0w1xw2x2...wMxM 如下图所示:
推导
我们…
坐标上升变分推断( Coordinate Ascent Variational Inference, CAVI)
变分推断是为了近似获得 P(Z∣X)P(Z | X)P(Z∣X) ,即隐状态的后验分布。 logP(X)logP(X,Z)−logP(Z∣X)logP(X,Z)q(Z)−logP(Z∣X)q(Z)\begin{aligned} log P(X) & log P(X, Z) - log P(Z | X) \\ & log \frac{P(X, Z)}{q(Z)} - log \frac{P(Z | X)}{q(Z)} …
概率论:多维随机变量及分布
多维随机变量及分布 X X X为随机变量, ∀ x ∈ R , P { X ≤ x } F ( x ) \forall x\in R,P\{X\le x\}F(x) ∀x∈R,P{X≤x}F(x) 设 F ( x ) F(x) F(x)为 X X X的分布函数,则 (1) 0 ≤ F ( x ) ≤ 1 0\le F(x)\le1 0≤F(x)≤1 &am…
概率论与数理统计:第四章:随机变量的数字特征
文章目录 Ch4. 随机变量的数字特征1. 数学期望E(X)(1)数学期望的概念1.离散型①一维离散型随机变量X的数学期望: E X EX EX②一维离散型随机变量的函数的期望: E [ g ( X ) ] E[g(X)] E[g(X)]③二维离散型随机变量的函数的期望: E [ g ( X , …
Relational Knowledge Distillation------论文阅读笔记(CVPR2019)
Relational Knowledge DistillationRKD (Abstractintroduction)2. Related Work3. Our Approach3.1 IKD(Individual KD)3.2 RKD(Relational knowledge distillation)3.2.1 Distance-wise distillation loss (距离蒸馏损失)3.2.2 Angle-wise distillation…
零阶矩、一阶矩、二阶矩、…
数学中矩的概念来自物理学。在物理学中,矩是表示距离和物理量乘积的物理量,表征物体的空间分布。矩在统计学和图像中都有很重要作用,我们常用的Adam优化器其全称为自适应矩估计优化器。本文将介绍各阶矩的理解和不同场景的应用。 Key Words&a…
统计动力学笔记(二)频谱密度与线性随机系统的动态准确性(自留用)
频谱密度与线性随机系统的动态准确性 1. 频谱密度2. 线性系统输出端的随机信号的频谱密度 1. 频谱密度
频谱密度是对相关函数 R ( t ) R(t) R(t)的傅里叶变换: S ( ω ) ∫ − ∞ ∞ R ( τ ) e − j ω τ d τ (1) S(\omega) \int_{-\infty} ^\infty R( \tau)…
【考研数学】概率论与数理统计 —— 第二章 | 一维随机变量及其分布(2,常见随机变量及其分布 | 随机变量函数的分布)
文章目录 引言三、常见的随机变量及其分布3.1 常见的离散型随机变量及其分布律(一)(0-1)分布(二)二项分布(三)泊松分布(四)几何分布(五࿰…
经管博士科研基础【19】齐次线性方程组
1. 线性方程组 2. 非线性方程组
非线性方程,就是因变量与自变量之间的关系不是线性的关系,这类方程很多,例如平方关系、对数关系、指数关系、三角函数关系等等。求解此类方程往往很难得到精确解,经常需要求近似解问题。相应的求近似解的方法也逐渐得到大家的重视。
3. 线…
单目标应用:基于蜘蛛蜂优化算法(Spider wasp optimizer,SWO)的微电网优化调度MATLAB
一、微网系统运行优化模型
微电网优化模型介绍:
微电网多目标优化调度模型简介_IT猿手的博客-CSDN博客
二、蜘蛛蜂优化算法
蜘蛛蜂优化算法(Spider wasp optimizer,SWO)由Mohamed Abdel-Basset等人于2023年提出,该…
数学期望,方差,标准差
数学期望
数学期望(也称为平均值)是用于衡量随机变量的平均值或预期值的统计量。它表示随机变量的平均取值。数学期望的计算公式如下: 数学期望 ( μ ) ∑ i 1 N x i ⋅ P ( x i ) \text{数学期望} (\mu) \sum_{i1}^{N} x_i \cdot P(x_i)…
贝叶斯估计:Cramér-Rao下界和Fisher信息
在概率统计和信息理论领域,Cramr-Rao下界(Cramr-Rao Bound)和Fisher信息(Fisher Information)是两个重要而密切相关的概念。它们在估计理论和信息量度量中发挥着关键作用。本文将深入探讨这两个概念的定义、关系以及它…
【计量经济学】固定效应、随机效应、相关随机效应
固定效应、随机效应、相关随机效应–潘登同学的计量经济学笔记 文章目录固定效应、随机效应、相关随机效应--潘登同学的计量经济学笔记固定效应模型固定效应的假设工作培训与废弃率的例子虚拟变量回归固定效应(FE)与一阶差分(FD)随机效应模型θ\thetaθ的取值范围工资方程的例子…
Qt之基于QCustomPlot绘制直方图(Histogram),叠加正态分布曲线
一.效果 二.原理
1.正态分布
高斯分布(Gaussian distribution),又名正态分布(Normal distribution),也称"常态分布",也就是说,在正常的状态下,一般的事物,都会符合这样的分布规律。 比如人的身高为一个随机变量,特别高的人比较少,特别矮的也很少,大部分都…
【概率方法】MCMC 之 Gibbs 采样
上一篇文章讲到,MCMC 中的 HM 算法,它可以解决拒绝采样效率低的问题,但是实际上,当维度高的时候 HM 算法还是在同时处理多个维度,以两个变量 x [ x , y ] \mathbf{x} [x,y] x[x,y] 来说,也就是同时从联合…
【贝叶斯分析】计算机科学专业博士作业二
1 第一题
1.1 题目
已知变量A和B的取值只能为0或1,A⫫𝑩,且𝑝(𝐴1)0.65,𝑝(𝐵1)0.77。C的取值与A和B有关,具体关系如下图所表:
ABP(C1|A,B)000.1010.99100…
矩母函数,概率生成函数, 随机变量的变换方法
这个标题真帅 Thanks Ni Zihan. 随机变量的变换方法总结概率生成函数 (probability-generating function, PGF)矩母函数(Moment Generating Function , MGF)矩母函数详细介绍 特征函数 Thanks Ni Zihan.
随机变量的变换方法总结
࿰…
随机过程 Brown 运动(上)
文章目录 随机过程 Brown 运动(上)基本概念与性质Guass 过程Brown 运动的鞅性质Brown 运动的 Markov 性 随机过程 Brown 运动(上)
基本概念与性质
例:(随机游走)设有一个粒子在直线上随机游动…
CVE-2021-41773 Apache HTTP Server漏洞复现
存在漏洞的版本:仅影响Apache HTTP Server 2.4.49版本 推荐环境:GitHub - blasty/CVE-2021-41773: CVE-2021-41773 playground
下载后:
docker-compose build && docker-compose up如果遇到: 则进入容器,修改…
机器学习笔记之狄利克雷过程(五)——基于狄利克雷过程的预测任务
机器学习笔记之狄利克雷过程——基于狄利克雷过程的预测任务引言回顾:从概率图角度观察狄利克雷过程关于随机测度G\mathcal GG的后验概率分布从指数族分布角度观察后验分布的性质关于θd(d1,2,⋯,D)\theta_d(d1,2,\cdots,\mathcal D)θd(d1,2,⋯,D)的补充将后验分…
机器学习算法--朴素贝叶斯(Naive Bayes)
1. 朴素贝叶斯(Naive Bayes)
朴素贝叶斯的介绍
朴素贝叶斯算法(Naive Bayes, NB) 是应用最为广泛的分类算法之一。它是基于贝叶斯定义和特征条件独立假设的分类器方法。由于朴素贝叶斯法基于贝叶斯公式计算得到,有着坚实的数学基础,以及稳定…
相关系数—如何从本质上理解协方差和相关系数(一)?
相关系数—如何从本质上理解协方差和相关系数(一)?前言一、先从公式说起二、非线性函数的变量和自变量之间的相关关系三 、协方差四 、协方差公与系统前言
“只有真正理解数学了才能从本质上理解某种现象和问题”,这句话不断激励…
3.6.3数据库系统-模式分解:是否保持函数依赖、保持函数依赖分解定义、无损分解、表格法、公式法
3.6.3数据库系统-模式分解:是否保持函数依赖、保持函数依赖分解定义、无损分解、表格法、公式法是否保持函数依赖保持函数依赖分解定义例题无损分解表格法例题公式法例题是否保持函数依赖
函数依赖是通过某一个维度可以函数决定另一个部分,这里在关系模…
8.1 假设验证的基本概念
学习目标:
要学习假设检验的基本概念,我会按照以下步骤进行: 了解假设检验的基本概念:假设检验是一种统计推断方法,用于判断某个假设是否成立。一般来说,假设检验包括原假设和备择假设两个假设,…
伯努利分布,二项分布和泊松分布以及最大似然之间的关系(未完成)
首先说伯努利试验 伯努利分布
伯努利试验说的是下面一种事件情况:在生活中,有一些事件的发生只有两种可能,发生或者不发生(或者叫成功或者失败),这些事件都可以被称为伯努利试验。
伯努利试验的概率分布称…
【随机数学】2021-9-14-概率统计与随机过程的学习记录与问题总结(一)(非笔记)
一、
确定性现象与随机现象; 随机现象中的统计规律;
随机试验:(观察一定条件,而且是可重复的条件的实现结果; E; 个人理解为对讨论随机事件概率时的规范化模块化操作,形成一套流程…
DW李宏毅机器学习——Task3
1、误差的来源
Where does the error come from ? 并不是模型越复杂,误差越小 error due to ‘bias’ and error due to ‘variance’ 理论上有一个最佳的函数f^\hat ff^,但我们没办法知道。利用训练数据,我们可以找到f∗f^*f…
离散Markov Chain序列及可视化
离散Markov Chain序列及可视化 文章目录 离散Markov Chain序列及可视化[toc]1 天气预测2 赌徒问题 1 天气预测
假设仅存在三种天气:晴天、阴天和雨天,每种天气状态构成的系统满足(齐次)马氏链过程,即下一期的天气状态仅取决于当前的天气状态…
博弈论(Nim游戏)
文章目录 博弈论(Nim游戏)Nim游戏方案台阶型 博弈论(Nim游戏)
文章首发于我的个人博客:欢迎大佬们来逛逛
Nim游戏
【模板】nim 游戏 - 洛谷 题目要求:给你 n 堆石子,两个人轮流取石子&#x…
详解维吉尼亚密码(附四种攻击策略)
目录
一. 介绍
二. 破解维吉尼亚密码
2.1 频率统计
2.2 提高型频率统计法
2.3 Kasiski攻击法
2.4 重合指数攻击法(index of coincidence method)
三. 小结 一. 介绍
我们知道英语字母的出现频率是有规律的,比如像下表: 掌…
强化学习复现笔记(3)Robbins-Monro算法证明
有个不知道具体表达式(也就是黑箱)的单调递增函数 M ( x ) M(x) M(x) 满足 0 < c 1 ≤ M ′ ( x ) ≤ c 2 0<c_1\leq M(x)\leq c_2 0<c1≤M′(x)≤c2,每输入 x x x 可以得到一个观测值 Y ( x ) M ( x ) w Y(x)M(x)w Y(x)M…
ORB_SLAM3 IMU预积分PreintegrateIMU
这篇博文主要分享ORB_SLAM3中Tracking::PreintegrateIMU(),其主要包括几个部分:
获得两帧之间的IMU数据中值积分IMU状态更新
关于IMU的理论推导参考:
ORB_SLAM3_IMU预积分理论推导(预积分项)ORB_SLAM3_IMU预积分理论推导(噪声分析)ORB_SLA…
【数理统计】假设检验的基本思想(一)
文章目录 选择题选择题 在参数假设检验中,Ⅱ风险是( C )。 A. P { 拒绝 H 0 ∣ H 0 为真 } P\{拒绝H_0|H_0为真\} P{
深度学习用于医学预后-第二课第三周1-3节-生存模型,生存函数
文章目录 生存模型生存函数有效生存函数 生存模型
本周,我们将讨论生存模式(survival model)。生存模型是一种特殊的模型我们关心事件发生的时间,比如从治疗到复发的时间,或者从诊断到死亡的时间
这是一个常见的问题…
概率有向图模型(一)
文章目录 前言概率有向图模型验证回到书中隐马尔可夫模型信念网络朴素贝耶斯 总结 前言
经过前面的复习,我们把李航老师的《统计学习方法》中的监督学习部分回顾了一遍,接下来我们在此基础上,开始学习邱锡鹏老师的《神经网络与深度学习》&am…
【人工智能】— 贝叶斯网络
【人工智能】— 贝叶斯网络 频率学派 vs. 贝叶斯学派贝叶斯学派Probability(概率):独立性/条件独立性:Probability Theory(概率论):Graphical models (概率图模型)什么是图模型(Grap…
概率论_概率公式中的分号(;)、逗号(,)、竖线(|) 及其优先级
目录
1.概率公式中的分号(;)、逗号(,)、竖线(|)
2.各种概率相关的基本概念
2.1 联合概率
2.2 条件概率(定义)
2.3 全概率(乘法公式的加强版)
2.4 贝叶斯公式
贝叶斯定理的公式推导 1.概率公式中的分号(;)、逗号(,)、竖线(|) ; 分号代表前后是两类…
联合高斯分布与条件高斯分布的相关性质(贝叶斯线性模型)
文章目录贝叶斯一般线性模型(*Bayesian general linear model*)贝叶斯线性模型下的联合高斯分布和边际分布贝叶斯线性模型下的条件高斯分布结合条件高斯分布的线性模型总结贝叶斯一般线性模型(Bayesian general linear model)
贝叶斯线性模型可以表征为: yHxw(1)\b…
人工智能数学课高等数学线性微积分数学教程笔记(目录)
前言
本文是对人工智能数学课高等数学线性微积分数学教程的学习笔记。由于之前的文章《人工智能数学课高等数学线性微积分数学教程笔记》篇幅过大,导致打开的时候加载缓慢,也不利于阅读,同时由于CSDN的限制原文已经不可更改,原文…
两个复高斯分布的乘积(高维)
假设p(x)∝CN(μ1,Σ1)CN(μ2,Σ2)p(\boldsymbol x) \propto \mathcal{CN}(\boldsymbol \mu_1, \boldsymbol \Sigma_1)\mathcal{CN}(\boldsymbol \mu_2, \boldsymbol \Sigma_2)p(x)∝CN(μ1,Σ1)CN(μ2,Σ2),有 p(x)∝exp{−(x−μ1)HΣ1−1(x−μ1)−(x−…
Rotation-Invariant-Distributions浅析
文章目录定义举例说明总结定义
这里给出旋转不变分布(Rotation-Invariant-Distributions)的两个定义
第一个定义 这里的旋转矩阵R\pmb RRRR就是正交阵。该定义比较直接,也比较形象。
第二个定义 该定义所述的spherically symmetric就是指旋转不变,上…
《统计学习方法》——隐马尔可夫模型(中)
概率计算算法
直接计算法
给定模型 λ ( A , B , π ) \lambda(A,B,\pi) λ(A,B,π)和观测序列 O ( o 1 , o 2 , ⋯ , o T ) O(o_1,o_2,\cdots,o_T) O(o1,o2,⋯,oT),计算观测序列 O O O出现的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)。最直接的方法就是…
信息熵、交叉熵、KL散度公式的简单理解
整理:我不爱机器学习
1 信息量
信息量是对信息的度量,就跟时间的度量是秒一样,考虑一个离散的随机变量 x 的时候,当观察到的这个变量的一个具体值的时候,我们接收到了多少信息呢?
例如听到太阳从东方升起…
JavaScript 数据处理 · 基本统计(文末附视频)
第 5 节 基本数据处理 基本统计
学习了如何对 JavaScript 中的数组数据进行操作之后,我们就要回到刚开始选择购买这本小册的目的了:使用 JavaScript 开发灵活的数据应用。既然说是数据应用,那么便离不开统计计算,而数组就可以说…
【计量经济学】时间序列预测
时间序列回归模型–潘登同学的计量经济学笔记 文章目录时间序列回归模型--潘登同学的计量经济学笔记时间序列数据时间序列回归模型静态模型(static model)有限分布滞后项模型(finite distributed lag model)冲击倾向长期倾向经典假设下OLS性质TS.1 线性于参数TS.2 无完全共线性…
兩獨立隨機變數之和的特徵函數
兩獨立隨機變數之和的特徵函數參考機率論 特性函數(1) - Properties,特徵函數(characteristic function)的定義為:φX(t)E(eit(X))\varphi_{X}(t)\operatorname{E}\left(e^{it(X)}\right)φX(t)E(eit(X))。 φXY(t)E(eit(XY))套用特徵函數的定義E…
第3章 随机变量的数字特征
第3章 随机变量的数字特征
[TOC] 随机变量的数字特征,是某些由随机变量的分布所决定的常数,它刻画了随机变量(或者说,刻画了其分布)的某一方面的性质。
3.1 数学期望(均值)与中位数
3.1.1 数…
大数定律及中心极限定理6
(今天继续努力学习!使劲学!)
目录
一、大数定律
1. 弱大数定理(辛钦大数定律)
2. 辛钦大数定律的推论-->伯努利大数定律
二、中心极限定理
1. 独立同分布的中心极限定理
2. 李雅普诺夫定理
3. 蒂莫夫-拉普…
数学基础--概率密度
首先考虑这样一个问题,你点了一个外卖,外卖说会在两个小时送达。那么送达的时间如下图(本次问题不考虑你进行催单和其他特殊情况,请勿抬杠)。 ,若外卖在第30分钟到60分钟送达那么概率是多少呢?…
多传感器融合定位九-基于滤波的融合方法Ⅰ其一
多传感器融合定位九-基于滤波的融合方法Ⅰ其一1. 滤波器的作用2. 概率基础知识2.1 概率、概率密度2.2 联合概率密度2.3 条件概率密度2.4 贝叶斯公式2.5 贝叶斯推断2.6 高斯概率密度函数2.7 联合高斯概率密度函数2.8 高斯随机变量的线性分布1. 滤波器的作用
滤波器的本质&#…
有关熵、相对熵(KL散度)、交叉熵、JS散度、Wasserstein距离的内容
写在前面
最近学了一些关于熵的内容,为增强自己对这些内容的理解,方便自己以后能够温习,随手记录了相关的介绍,可能有不对的地方,敬请谅解。
信息量 任何事件都会承载一定的信息,事件发生的概率越大&…
概率论:数字特征与极限定理——方差与标准差
方差是怎样产生的?:
由此得出方差的标准定义: 可以这样简记:E(x)只是常数,直接拿出来.x^2*f(x)就是在求E(x^2),所以是E(x^2)-E(x)^2。 方差的一些性质: 可以这样证:D(xy)E(xy-E(xy))^2E(x-E(x)…
rank(A)=rank(A^TA)
Let x∈N(A)x\in N(A)x∈N(A) where N(A)N(A)N(A) is the null space of AAA. Hence Ax0⇒ATAx0⇒x∈N(ATA)Ax0 \Rightarrow A^TAx0 \Rightarrow x\in N(A^TA)Ax0⇒ATAx0⇒x∈N(ATA)
It means that N(A)⊂N(ATA)N(A)\subset N(A^TA)N(A)⊂N(ATA). On the other hand, suppose …
统计学专业未来从事大数据方向有优势吗?
根据现在工业界的大数据就业情况来说(对于一般同学而非牛人),统计从事大数据来说优势小。对一般数据分析甚至建模有一定优势。
我这篇回答面向的是大部分水平还可以的统计本科生,他们也努力学习了专业课,编程基础一般…
【概率论】常用连续分布(一)
文章目录 选择题 选择题 设随机变量 X~N(μ, 16) , Y~N(μ, 25), 则()。 A. 对任意的μ,有 P{X≤μ-4} P{Y≥μ5}. B. 对任意的μ,有 P{X≤μ-4}<P{Y≥μ5}. C. 只对μ的个别值,有 P{X≤μ-4}P{Y≥μ5}. D. 对任意的μ,有 P{X≤…
数据分析技能点-正态分布和其他变量分布
在数据驱动的世界里,了解和解释数据分布是至关重要的。不同类型的数据分布,如正态分布、二项分布和泊松分布,具有不同的特性和应用场景。这些分布不仅在统计学和数据科学中有广泛应用,而且在日常生活和商业决策中也起着关键作用。 文章目录 正态分布正态分布和偏差其他常见…
正态分布的概率密度函数|多种正态分布检验|Q-Q图
正态分布的概率密度函数(Probability Density Function,简称PDF)的函数取值是指在给定的正态分布参数(均值 μ 和标准差 σ)下,对于特定的随机变量取值 x,计算得到的概率密度值 f(x)。这个值表示…
alpha-beta滤波
The alpha - beta - gamma filter
import numpy as np
import matplotlib.pyplot as plt
import randommid, sigma 0, 0.1
totalTimeStep 300
noise np.random.normal(mid, sigma, totalTimeStep) * 100dt 1
v 0
x_lf 0
# 测量值
x 0
x_lf_list []
x_list []
# 估计值…
偏度系数与偏态系数的简要阐述
偏度系数:描述分布偏离对称性程度的一个特征数。当分布左右对称时,偏度系数为0;当偏度系数大于0时,即重尾在右侧时,称该分布为右偏(正偏态);当偏度系数小于0,即重尾在左侧…
@[计算方法]蒙特卡罗投点
蒙特卡洛方法:
from random import random
from math import sqrtDARTS 1000
hits 0.0
for i in range(1,DARTS1):x,y random(),random()dist sqrt(x ** 2y **2)if dist < 1.0:hits hits 1
pi 4 * (hits/DARTS)
print("Pi值是{}".format(pi))解…
朴素贝叶斯,支持向量积,Fisher分类器的简单数学原理推导
1.朴素贝叶斯算法(Naive Bayes) 2.支持向量机(Support Vector Machine,SVM)的wolf对偶模型 3.Fisher分类器or线性判别分析(Linear Discriminant Analysis,LDA)
入门机器学习(西瓜书+南瓜书)贝叶斯分类器总结(python代码实现)
入门机器学习(西瓜书南瓜书)贝叶斯分类器总结(python代码实现)
一、贝叶斯分类器
1.1 通俗理解
先来看两个公式 P(AB)P(A)P(B)(1)P(AB)P(A)P(B) (1)P(AB)P(A)P(B)(1&a…
如何理解对数差异、比对数几率
文章目录 对数几率逻辑回归“对数差异比”(或常称为对数几率,log odds)是一种表示和处理概率的方法。 对数差异比(对数几率): 对于一个概率值 ( p ),它的对数几率定义为: [ \text{log odds} = \log \left( \frac{p}{1-p} \right) ] 这里,( p ) 是某事件发生的概率,而 (…
AI算法岗面试问题记录1
记录一下面试算法岗过程中问到的问题,部分想不起了。
1.交叉熵是怎么回事?公式是什么?
在机器学习中,我们需要评估label和predicts之间的差距,使用KL散度刚刚好,即 由于KL散度中的前一部分−H(y)不变&…
SPSS两独立样本t检验
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件请点击此链接下…
雅克比矩阵在机器人运动学中的应用
以六轴机械臂为例,设机械臂关节空间为q,位置矩阵为p,速度矩阵为v q [ q 0 , q 1 , q 2 , q 3 , q 4 , q 5 ] q[q_0,q_1,q_2,q_3,q_4,q_5] q[q0,q1,q2,q3,q4,q5] p [ x , y , z ] T [ f x ( q ) f y ( q ) f z ( q ) ] p[x,y,z…
优思学院|六西格玛真题讲解:泊松分布的计算方法
优思学院在早前的文章曾经介绍过二项分布,二项分布是离散型机率模型中最有名的一个,其次就是泊松分布(Poisson Distribution),它可以看成为二项分布的一种极限情形,由法国数学家西莫恩德尼泊松在1838年时发…
【考研数学】概率论与数理统计 | 第一章——随机事件与概率(2)
文章目录 引言四、概率基本公式4.1 减法公式4.2 加法公式4.3 条件概率公式4.4 乘法公式 五、事件的独立性5.1 事件独立的定义5.1.1 两个事件的独立5.1.2 三个事件的独立 5.2 事件独立的性质 写在最后 引言
承接上文,继续介绍概率论与数理统计第一章的内容。 四、概…
【博弈论】混合策略纳什均衡
上一章中遇到了划线法无法找到均衡的情况,例如盖硬币博弈,盖方盖硬币,猜方猜正反。那是因为考虑的都是纯策略,就是每个策略要么选,要么不选。本章考虑混合策略,就是每个策略都有一个选择的概率。 考虑还是这…
【数据处理】Python:实现求条件分布函数 | 求平均值方差和协方差 | 求函数函数期望值的函数 | 概率论
猛戳订阅! 👉 《一起玩蛇》🐍 💭 写在前面:本章我们将通过 Python 手动实现条件分布函数的计算,实现求平均值,方差和协方差函数,实现求函数期望值的函数。部署的测试代码放到文后了&…
11.10~11.15置信区间,均值、方差假设检验,正态,t,卡方,F分布,第一第二类错误
置信度,置信区间
给定一个置信度,就可以算出一个置信区间。
如果给的置信度越大,那么阿尔法就越小
给的置信度越小,那么α就越大,那么
考虑精确性,希望区间长度尽可能小,所以是取正态的中间…
[第一章]1.1 样本空间与随机事件
样本空间与随机事件 今日听课状态:心不在焉,但是没关系,如我开头所说,只要习题会做就行。 今天的这部分内容带有大量的高中的集合论的知识。因此从道理上来说,这门课的学习难度并不会很大。但是这也是相对的,如果不学当…
机器学习课后习题 ---数学基础回顾
(一)选择题
1.函数y=1/(x+1)是
A.偶函数 B.奇函数 C.单调函数 D.无界函数 2.设f(sin(x/2)=cosx+1,则f(x)为()
A.2x-2 B.2-2x C.1+2 …
中心极限定理|独立同分布|大数定律
中心极限定理(Central Limit Theorem,CLT)是统计学中的一个重要概念,它描述了当从总体中抽取大量独立随机样本,并计算这些样本的均值时,这些均值的分布将近似于正态分布,无论原始总体的分布形状…
【AI】机器学习——朴素贝叶斯
文章目录 2.1 贝叶斯定理2.1.1 贝叶斯公式推导条件概率变式 贝叶斯公式 2.1.2 贝叶斯定理2.1.3 贝叶斯决策基本思想 2.2 朴素贝叶斯2.2.1 朴素贝叶斯分类器思想2.2.2 条件独立性对似然概率计算的影响2.2.3 基本方法2.2.4 模型后验概率最大化损失函数期望风险最小化策略 2.2.5 朴…
数理统计的基本概念(二)
文章目录 抽样分布几个重要分布 Γ \Gamma Γ 分布 β \beta β 分布 χ 2 \chi^2 χ2 分布 t t t 分布 F F F 分布 分位数 参考文献 抽样分布
所谓抽样分布是指统计量的概率分布。确定统计量的分布是数理统计学的基本问题之一。
几个重要分布 Γ \Gamma Γ 分布 若随机变量 …
朋友圈大佬都去读研了,这份备考书单我码住了
作者简介: 辭七七,目前大二,正在学习C/C,Java,Python等 作者主页: 七七的个人主页 文章收录专栏: 七七的闲谈 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖…
(一)探索随机变量及其分布:概率世界的魔法
文章目录 🍋引言🍋什么是随机变量?🍋离散随机变量🍋连续随机变量 🍋随机变量的概率分布🍋离散概率分布🍋0-1分布(Bernoulli分布)🍋二项分布&#…
19. 概率与统计 - 频率派贝叶斯派
文章目录 频数和频率频率派视角下的概率贝叶斯派视角下的概率Hi, 您好。我是茶桁。
本节课,咱们开始学习「概率&统计」的部分,说实话,这个部分是我觉得最有意思的地方。
在之前的课程中,除了导论课给大家过了一遍通识性的各个领域的一些知识之外,我们已经上过了关于…
PT@古典概型@等概率模型
文章目录 abstract等可能概型(古典概型)🎈古典型概率公式基本性质导出性质例 抽样方式放回抽样不放回抽样 m m m次取求不放回和一次性取 m m m个球例:取色球和古典概型 古典概型经典问题放球问题两人同一天生日问题 超几何分布概型整除取数问题 抽签问题取最大号球问…
概率论与数理统计(第一章 概率论的基本概念)
文章目录 第一章 概率论的基本概念一、随机试验二、事件的概率 第一章 概率论的基本概念
一、随机试验
随机试验特点: ①可以在相同的条件下重复进行 ②每次试验的可能结果不止一个,并且能提前预测所有的可能结果 ③在未进行试验前不知道哪一个结果会出…
大数据HCIE成神之路之数学(3)——概率论
概率论 1.1 概率论内容介绍1.1.1 概率论介绍1.1.2 实验介绍 1.2 概率论内容实现1.2.1 均值实现1.2.2 方差实现1.2.3 标准差实现1.2.4 协方差实现1.2.5 相关系数1.2.6 二项分布实现1.2.7 泊松分布实现1.2.8 正态分布1.2.9 指数分布1.2.10 中心极限定理的验证 1.1 概率论内容介绍…
MATLAB实现相关性分析
目录 一.基本理论 二.两类相关系数的对比
三.相关系数的假设检验
四.MATLAB的相关操作
五.其他有关的一些列技巧
六.案例展示
七.实战操作 一.基本理论
所谓相关系数,本质上是来衡量两组数据的关系大小——对应呈现函数关心的两种变量,那么我们可以…
优思学院|什么是精益生产管理?从一个生活上的故事出发来说明。
你关掉电脑,离开办公室。
一个小时后,你进入家门和孩子们在一起。
你和家人一起吃晚饭。
你的老板打电话来查看你的项目进展。
你哄孩子入睡并给他们读个故事。 作为一个负责任的父母,你想要与孩子们的互动时间增加并提高生活的质量&…
回归算法优化过程推导
假设存在一个数据集,包含工资、年龄及贷款额度三个维度的数据。我们需要根据这个数据集进行建模,从而在给定工资和年龄的情况下,实现对贷款额度的预测。其中,工资和年龄是模型构建时的两个特征,额度是模型输出的目标值…
概率论小课堂:伯努利实验(正确理解随机性,理解现实概率和理想概率的偏差)
文章目录 引言I 伯努利试验1.1 伯努利分布(二项式分布)1.2 数学期望值(简称期望值)1.3 平方差(简称方差)1.4 标准差1.5 小结引言
假设买彩票中奖的概率是一百万分之一,如果要想确保成功一次,要买260万次彩票。你即使中一回大奖,花的钱要远比获得的多得多。
很多人喜…
模式识别 —— 第二章 参数估计
模式识别 —— 第二章 参数估计 文章目录模式识别 —— 第二章 参数估计最大似然估计(MLE)最大后验概率估计(MAP)贝叶斯估计最大似然估计(MLE)
在语言上:
似然(likelihood…
“手撕“ BootStrap 方法
文章目录Part.I IntroductionChap.I bootstrap 方法简介Chap.II 预备知识Part.II 非参数 bootstrap 方法Chap.I 估计量标准误差的bootstrap估计Chap.II bootstrap 置信区间Chap.III bootstrap-t 法Chap.IV 一个实例Part.III 参数 bootstrap 方法Chap.I 一个实例Part.I Introduc…
卡尔曼滤波 - 状态空间模型中的状态方程
卡尔曼滤波 - 状态空间模型中的状态方程
flyfish
状态方程和观测方程统称为状态空间模型
位移 位移Δxxf−x0\text { 位移}\Delta xx_f-x_0位移Δxxf−x0 x0x_0x0 是起始位置 xfx_fxf 是终止位置 在坐标轴里,右边是正,左边是负
面积等于物体…
干货分享:小红书商业化+微信社区运营,引流自动裂变拓客方案
干货分享:小红书商业化微信社区运营,引流自动裂变拓客方案 背景:2023为止小红书基本已是当代年轻人都会下载和使用的软件了,小红书是生活方式平台和消费决策入口,通过智能机器人学习和对用户的精准智能匹配走红&#x…
贝叶斯统计中的边缘分布
概率论与数理统计中的边缘分布
假设有二维随机变量 ( X , Y ) (X,Y) (X,Y)具有分布函数 F ( x , y ) F(x,y) F(x,y),其中 X , Y X,Y X,Y都是随机变量,也有各自的分布函数,将它们各自的分布函数分别记为 F X ( x ) , F Y ( y ) F_X(x),F_Y(y)…
马尔可夫链蒙特卡罗算法(MCMC方法)
MCMC方法是什么
具体而言,假设我们要计算积分 μ ∫ S h ( θ ) π ( θ ∣ x ) d θ \mu\int_Sh(\theta)\pi(\theta|x)d\theta μ∫Sh(θ)π(θ∣x)dθ如果后验分布 π ( θ ∣ x ) \pi(\theta|x) π(θ∣x)难以直接抽样,那么我们就可以构造一条马氏…
判断无穷积分是绝对收敛还是条件收敛---练习题
本篇文章重点讨论一般无穷积敛散性的判别。(即被积函数在所积区间符号不定,既有正的,也有负的) 不论是绝对收敛还是条件收敛,它本身一定是
收敛的。
狄利克雷判别法: 例题: 首先,将…
【结构与算法】—— 游戏概率常用算法整理 | 游戏中的常见概率设计分析
📢博客主页:肩匣与橘📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢本文由肩匣与橘编写,首发于CSDN🙉📢生活依旧是美好而又温柔的,你也是✨ …
Towards a Deep and Unified Understanding of Deep Neural Models in NLP
这篇文章比较难,需要较多的概率论和信息论知识,论文中公式推导给的不是特别多,有些过程并没有做推导,因此不是太能理解,不过大概意思是能懂的。 论文提出了一种知识量计算方法,通过计算每个输入的知识量&am…
随机过程——马尔科夫链
Markov过程
已知现在的状态,未来状态与过去的状态无关。 P(X(tn1)≤xn1∣X(t1)x1,...,X(tn)xn)P(X(tn1)≤xn1∣X(tn)xn)P(X(t_{n1})≤x_{n1}|X(t_1)x_1,...,X(t_n)x_n) P(X(t_{n1})≤x_{n1}|X(t_n)x_n)P(X(tn1)≤xn1∣X(t1)x1,...,X(tn)xn)P(X(tn1)…
Kalman滤波(Part-2:标量形式)
在开始之前,先回顾一下正交、不相关和独立之间的联系与差别 正交 随机变量:R(x,y)E[xy]\mathcal R(x, y) \mathbb E[xy]R(x,y)E[xy]为相关函数,若R(xy)0\mathcal R(xy)0R(xy)0,则认为x,yx,yx,y正交。(类比内积,注意&a…
2023年计算机考研数学一考试大纲
2022年计算机考研数学一考纲对外公布时间在2021年11月30日,2022年考研之前考纲基本使用的是2017年版本的考研数学大纲,预计2023年计算机考研数学一也会继续使用2022年考纲,下文就是2022年计算机考研数学一的考纲详情,可供参考。
…
2023年计算机考研数学考一还是二?考研数学一二三区别
2023年计算机专业考研数学基本是考数学一,除此之外,计算机专业考研科目有英语一、政治和专业课,共计四门,总分是500分,录取分基本在300分以上。
2023年计算机专业考研科目是什么呢?
计算机科学与技术学科采用全国统…
Advanced ML Chapter12-Multi-Task Learning
下面的要训练m次。 假设所有任务之间,有共同的一个参数ω0. ωi ω0 Δωi的意思是ωi在ω0的基础上,有一个变化量 Δωi λ Δ||ω||2加了正则想,如果多任务的相关性比较强,那么loss就比较低,训练的比较好。但是…
彻底搞明白概率论:事件间的关系与运算;频率与概率
文章目录事件间的关系事件间的运算事件间的运算法则概率描述性定义统计性定义频率频率的性质频率是否能够作为概率呢?公理化定义概率的重要性质事件间的关系 注意互斥关系和对立关系: 互斥关系是:只要 A,BA,BA,B 不同时发生(不存在…
5003笔记 Statistic Chapter9-Tree and Ensemble methods
R1,R2,R3就是leaf node页节点。internal node内节点,就是判断的条件。 决策树的评价指标是RSS,对于决策树来说,我们如何找他的预测值呢?对于回归树而言,我们会通过recursive binary splitting和greedy algorithm 树…
概率统计·大数定律及中心极限定理【大数定律、中心极限定律】
这一章的学习更多的是为后面的知识作铺垫,所以内容比较少🍘🍘🍘(当然也减轻一点复习的负担🤗🤗🤗)
依概率收敛 需要概率P极限趋近于1
切比雪夫不等式的特殊情况
前提&…
机器学习中的数学基础(二)
机器学习中的数学基础(二)2 线代2.1 矩阵2.2 矩阵的秩2.3 内积与正交2.4 特征值与特征向量2.5 SVD矩阵分解2.5.1 要解决的问题2.5.2 基变换2.5.3 特征值分解2.5.4 奇异值分解(SVD)在看西瓜书的时候有些地方的数学推导(…
t-SNE数据降维可视化
t-SNE数据降维可视化 – 潘登同学的Machine Learning笔记 文章目录t-SNE数据降维可视化 -- 潘登同学的Machine Learning笔记t-SNE的基本思想SNE(Stochastic Neighbor Embedding)SNE的主要缺点距离不对称存在拥挤现象如何确定σ\sigmaσ总结t-sne代码实现对比t-sne与UMAP是最近遇…
变分自编码器VAE的数学原理
变分自编码器(VAE)是一种应用广泛的无监督学习方法,它的应用包括图像生成、表示学习和降维等。虽然在网络架构上经常与Auto-Encoder联系在一起,但VAE的理论基础和数学公式是截然不同的。本文将讨论是什么让VAE如此不同,并解释VAE如何连接“变…
计算方法 2.非线性方程和方程组的数值解法
主要是学习各种近似解法。 求根步骤: 二分法: 迭代法: 就是把f(x)0变幻成了xu(x),我解出后面那个方程也就是解出了f(x)0.而后面那个很经典,就是不懂点嘛。 P阶收敛就是wi1wi^p*C(这个c就是歌姬吧,主要是p&a…
机器学习笔记之生成模型综述(三)生成模型的表示、推断、学习任务
机器学习笔记之生成模型综述——表示、推断、学习任务引言生成模型的表示任务从形状的角度观察生成模型的表示任务从概率分布的角度观察生成模型的表示任务生成模型的推断任务生成模型的学习任务引言
上一节介绍了从监督学习、无监督学习任务的角度介绍了经典模型。本节将从表…
非参数检验方法,核密度估计简介
在20世纪,统计学还处于起步阶段计算机还不是那么流行的时候,假设正态分布是生成数据的标准。这主要是因为在那个所有结果都是手工计算的时代,正态分布可以使计算不那么繁琐。 但在这个大数据时代,随着计算能力的提高,数…
机器学习100天(三十五):035 贝叶斯公式
《机器学习100天》完整目录:目录 机器学习100天,今天讲的是:贝叶斯公式!
好了,上一节介绍完先验概率、后验概率、联合概率、全概率后,我们来看这样一个问题:如果我现在挑到了一个瓜蒂脱落的瓜,则该瓜是好瓜的概率多大?
显然,这是一个计算后验概率的问题,根据我们之…
Stochastic Approximation 随机近似方法的详解之(一)
随机近似的定义:它指的是一大类随机迭代算法,用于求根或者优化问题。 Stochastic approximation refers to a broad class of stochastic iterative algorithms solving root finding or optimization problems. temporal-difference algorithms是随机近…
ML | 4.朴素贝叶斯
基于概率论的分类方法:朴素贝叶斯 文章目录 基于概率论的分类方法:朴素贝叶斯概述条件概率贝叶斯公式 朴素贝叶斯分类器2个假设Example:文本分类欢迎关注公众号【三戒纪元】 概述
朴素贝叶斯可以处理多类别问题,在数据较少的情况下仍然有效&…
概率论小课堂:泊松分布(完善你对随机性的认识,特别是对风险防范的认识)
文章目录引言I 泊松分布1.1 概率计算公式1.2 应对随机性,需要的冗余比平均值要大1.3 池子越大,越能抵消随机性带来的误差引言
伯努利试验:解释了随机事件的发生概率在理论和现实中的差距泊松分布:进一步完善你对随机性的认识&…
3D数学系列之——再谈特卡洛积分和重要性采样
目录一、前篇文章回顾二、积分的黎曼和形式三、积分的概率形式(蒙特卡洛积分)四、误差五、蒙特卡洛积分计算与收敛速度六、重要性采样七、重要性采样方法和过程八、重要性采样的优缺点一、前篇文章回顾 在前一篇文章3D数学系列之——从“蒙的挺准”到“蒙…
概率统计_协方差的传播 Covariance Propagation
1. 方差的传播 误差的传播是指分析在形如的关系中,参量误差(x)对变量误差(y)的影响有多大。误差的传播与函数的微分紧密相关,本质是在利用当Δ x 不大时,。 方差计算公式: X为变量,为总体均值,N为总体例数。求变量X与均值的差的平方再求平均值,即得到方差。方差…
概率统计Python计算:一元线性回归应用——控制
对一元线性回归模型x{x1,x2,⋯,xn}x\{x_1,x_2,\cdots,x_n\}x{x1,x2,⋯,xn},Y{Y1,Y2,⋯,Yn}Y\{Y_1,Y_2,\cdots,Y_n\}Y{Y1,Y2,⋯,Yn},YiY_iYi~N(axib,σ2),i1,2,⋯,nN(ax_ib, \sigma^2),i1,2,\cdots,nN(axib,σ2)&a…
概率统计Python计算:一元线性回归回归系数a=0的假设检验
设试验样本数据x(x1,x2,⋯,xn)x(x_1,x_2,\cdots,x_n)x(x1,x2,⋯,xn),Y(Y1,Y2,⋯,Yn)Y(Y_1,Y_2,\cdots,Y_n)Y(Y1,Y2,⋯,Yn),若拒绝假设 H0:a0(H1:a̸0)H_0: a0(H_1:a\not0)H0:a0(H1:a0) 则诸YiY_iYi~N(axb,σ2)N(axb, \sigma^2)N(a…
概率统计Python计算:双因素无重复试验方差分析
双因素无重复试验方差分析的数据模型XXX是一个rsr\times srs的矩阵,XijX_{ij}Xij~N(μij,σ2)N(\mu_{ij},\sigma^2)N(μij,σ2)。令X‾1rs∑i1r∑j1sXij\overline{X}\frac{1}{rs}\sum\limits_{i1}^r\sum\limits_{j1}^{s}X_{ij}Xrs1i1∑rj1∑sXij&#x…
概率统计Python计算:双因素等重复试验方差分析
双因素等重复试验的数据模型XXX是一个结构为rstr\times s\times trst的3-维矩阵(张量),其中XijkX_{ijk}Xijk取自于总体指标N(μij,σ2)N(\mu_{ij},\sigma^2)N(μij,σ2),i1,2,⋯,r,j1,2,⋯,s,k1,2,⋯,ti1,2,\cdots,r,j1,2,\cd…
概率统计Python计算:双正态总体方差比双侧假设的F检验
对两个独立的正态总体XXX~N(μ1,σ12)N(\mu_1,\sigma_1^2)N(μ1,σ12)和YYY~N(μ2,σ22)N(\mu_2, \sigma_2^2)N(μ2,σ22),检验双侧假设 H0:σ12/σ221,H1:σ12/σ22̸1H_0:\sigma_1^2/\sigma_2^21,H_1:\sigma_1^2/\sigma_2^2\not1H0:σ12/σ221,H1…
概率统计Python计算:双正态总体未知总体方差总体均值差单侧假设的T检验
设总体XXX~N(μ1,σ2)N(\mu_1,\sigma^2)N(μ1,σ2),YYY~N(μ2,σ2)N(\mu_2, \sigma^2)N(μ2,σ2)相互独立,σ2\sigma^2σ2未知。为检验右侧假设H0:μ1−μ2≤δ,H1:μ1−μ2>δH_0:\mu_1-\mu_2\leq\delta,H_1:\mu_1-\mu_2>\deltaH0:μ1−μ…
概率统计Python计算:单个正态总体均值单侧假设的T检验
正态总体的方差σ2\sigma^2σ2未知的情况下,对总体均值μ≤μ0\mu\leq\mu_0μ≤μ0(或μ≥μ0\mu\geq\mu_0μ≥μ0)进行显著水平α\alphaα下的假设检验,检验统计量X‾−μ0S/n\frac{\overline{X}-\mu_0}{S/\sqrt{n}}S/nX−…
概率统计Python计算:单个正态总体均值双侧假设的Z检验
用p值法计算假设H0H_0H0的双侧检验,设aaa,bbb分别是检验统计量分布对应显著水平α\alphaα的左、右分位点,F(x)F(x)F(x)和S(x)S(x)S(x)分别为检验统计量的分布函数和残存函数。若检验统计量观测值γ\gammaγ落在其分布的均值右边࿰…
【深度学习笔记】04 概率论基础
04 概率论基础 概率论公理联合概率条件概率贝叶斯定理边际化独立性期望和方差模拟投掷骰子的概率随投掷次数增加的变化 概率论公理
概率(probability)可以被认为是将集合映射到真实值的函数。 在给定的样本空间 S \mathcal{S} S中,事件 A \m…
【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布(2,常见的二维随机变量及二维变量的条件分布和独立性)
文章目录 引言四、常见的二维随机变量4.1 二维均匀分布4.2 二维正态分布 五、二维随机变量的条件分布5.1 二维离散型随机变量的条件分布律5.2 二维连续型随机变量的条件分布 六、随机变量的独立性6.1 基本概念6.2 随机变量独立的等价条件 写在最后 引言
有了上文关于二维随机变…
正态分布的概率密度函数|正态分布检验|Q-Q图
正态分布的概率密度函数(Probability Density Function,简称PDF)的函数取值是指在给定的正态分布参数(均值 μ 和标准差 σ)下,对于特定的随机变量取值 x,计算得到的概率密度值 f(x)。这个值表示…
Z检验scipy.stats.norm的相关计算
Z检验(Z-test)是一种用于检验一个样本的均值是否与已知的总体均值相等的统计方法。它通常用于以下情况: 总体参数已知: 当总体的均值和标准差已知时,可以使用Z检验来确定样本均值是否与总体均值相等。 大样本ÿ…
多组试验时正态分布标准差估计公式
本文介绍如何通过多组试验数据来估计正态总体的标准差. 一,各组试验次数相等 设正态总体X~N(μ,σ),其中均值μ和标准差σ未知.今有m组样本,每组样本大小n相等,其试验数据如下:求标准差σ的估计σ. 多组试验时正态分布标准差估计公式 - 百度学术
【总结】两个独立同分布的随机变量相加还是原来的分布吗?
二项分布,泊松分布,正态分布,卡方分布,具有独立可加性。 图源自没咋了,面哥课程。
【什么是高斯分布?还有什么分布?他们的用途是什么?】
高斯分布
高斯分布,也被称为正态分布或钟形曲线,是统计学中最为常见和重要的连续概率分布之一。高斯分布的概率密度函数(PDF)是: 其中: ( x ) 是变量( \mu ) 是分布的均值(mean)( \sigma ) 是标准差(standard deviation)( \sigma^2 ) 是方差(variance)以下是关于高…
积分表二(高等数学同济版中所有的积分公式)
文章目录 含有 x − a x a \sqrt{\pm \frac{x-a}{xa}} xax−a 或者 ( x − a ) ( b − x ) \sqrt{(x-a)(b-x)} (x−a)(b−x) 的积分含有三角函数函数的积分含有反三角函数的积分 (其中 a > 0 a>0 a>0)含有指数函数的积分含有对数函数的积分含有双曲函数的…
概率测度理论方法(第 2 部分)
一、说明 欢迎回到这个三部曲的第二部分!在第一部分中,我们为测度论概率奠定了基础。我们探索了测量和可测量空间的概念,并使用这些概念定义了概率空间。在本文中,我们使用测度论来理解随机变量。 作为一个小回顾,在第…
【知识串联】概率论中的值和量(随机变量/数字特征/参数估计)【考研向】【按概率论学习章节总结】
就我的概率论学习经验来看,这两个概念极易混淆,并且极为重点,然而,在概率论的前几章学习中,如果只是计算,对这方面的辨析不清并没有问题。然而,到了后面的参数估计部分,却可能出现问…
moea中return, risk的计算
M - np.sum(np.dot(x.T, r))为什么return的定义是这样的?其中x是一个向量,表示对每个股份的投资比例,r是各个股份的回报return的均值 V np.sum(np.dot(x, x.T) * np.dot(s, s.T) * c)为什么risk的定义是这样的?其中x是一个向量&…
MBA-数学题概念和公式
{}公差大于零的等差数列:多个数字组成的数列,两两之间差相等,且后值减前值大于0,如:{-2,0,2,4}为公差数列为2的等差数列.因数是指整数a除以整数b(b≠0) 的商正好是整数而没有余数,10的因数为 2和5圆柱体表面积 2πr 2πrh球体表名…
Gumbel 重参数化相关性质证明
Gumbel 的采样过程: z a r g m a x i { g i l o g ( π i ) } , g i − l o g ( − l o g ( u i ) ) , u i ∼ U ( 0 , 1 ) zargmax_i \{g_i log(\pi_i)\}, g_i -log(-log(u_i)),u_i\sim U(0, 1) zargmaxi{gilog(πi)},gi−log(−log(ui)),ui∼U(0…
为啥$p(w|D)=p(y|X,w)$?
为啥 p ( w ∣ D ) p ( y ∣ X , w ) p(w|D)p(y|X,w) p(w∣D)p(y∣X,w)? p ( w ∣ X , y ) p ( w ∣ D ) p(w|X,y)p(w|D) p(w∣X,y)p(w∣D), p ( w ∣ D ) p ( D , w ) / p ( D ) p(w|D)p(D,w)/p(D) p(w∣D)p(D,w)/p(D)为啥 p ( D ∣ w ) p ( y ∣ X , w ) p(D|…
概率中的50个具有挑战性的问题[03/50]:轻率的陪审员
一、说明 我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克莫斯特勒(Frederick Mosteller)的《概率论中的五十个具有挑战性的问题与解决方案》(Fifty Challenge Problems in Probability with Solutions)一书。我认为…
概率中的50个具有挑战性的问题[02/50]:连续获胜
一、说明 我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克莫斯特勒(Frederick Mosteller)的《概率论中的五十个具有挑战性的问题与解决方案》(Fifty Challenge Problems in Probability with Solutions)一书。我认为…
数理统计的基本概念(一)
文章目录 总体、样本与统计量总体及其分布样本及其分布统计量统计量概念样本矩顺序统计量及其分布样本中位数与样本极差经验分布函数 参考文献 总体、样本与统计量
总体及其分布
在数理统计中,称所研究的对象的全体为总体,总体中的元素称为个体。若总体…
大数定律中心极限定理
1.切比雪夫不等式
切比雪夫不等式可以对随机变量偏离期望值的概率做出估计,这是大数定律的推理基础。以下介绍一个对切比雪夫不等式的直观证明。
1.1 示性函数
对于随机事件A,我们引入一个示性函数 I A { 1 , A发生 0 , A不发生 I_A\begin{cases} 1&…
SPSS相关统计学知识精要回顾-大家都来做做
很多学生问我,学SPSS如果想深入学,那么统计学原理应该掌握到什么样的水准,我想说的是,如果真的想融会贯通,而不是短暂过关,那么应该具备一定的统计学基础,但是统计学知识也不是面面俱到都要去学…
Csiszár divergences
Csiszr divergences
熵函数
熵函数(entropy function) φ : R → R \varphi: \mathbb{R}_{} \to \mathbb{R}_{} φ:R→R,他是凸函数,正的(?),下半连续函数,并且 φ ( 1 ) …
概率论与数理统计————古典概型、几何概型和条件概率
一、古典概型
特点
(1)有限性:试验S的样本空间的有限集合
(2) 等可能性:每个样本点发生的概率是相等的
公式:P(A) A为随机事件的样本点数;S是样本…
一文梳理金融风控建模全流程(Python)
▍目录
一、简介 风控信用评分卡简介 Scorecardpy库简介
二、目标定义与数据准备 目标定义 数据准备
三、安装scorecardpy包
四、数据检查
五、数据筛选
六、数据划分
七、变量分箱 卡方分箱 手动调整分箱
八、建立模型 相关性分析 多重共线性检验VIF KS和AUC …
概率统计Python计算:双正态总体方差比的单侧区间估计
对计算双正态总体方差比的双侧区间估计的函数sigma2RatioBounds(详见博文《双正态总体方差比的双侧区间估计》)稍加修改,可得下列计算双正态总体方差比的单侧区间估计的函数sigma2RatioBound。
def sigma2RatioBound(d, dfn, dfd …
概率统计Python计算:双正态总体均值差的单侧区间估计
与计算双正态总体均值差的双侧区间估计相仿,我们可以调用单正态总体均值的单侧置信区间的计算函数muBound(详见博文《单个正态总体均值的单侧区间估计》)计算双正态总体均值差的单侧区间估计:只需对参数mean传递样本均值差x‾−y‾…
概率统计Python计算:单个正态总体均值的单侧区间估计
计算单个总体XXX~N(μ,σ2)N(\mu,\sigma^2)N(μ,σ2)的参数μ\muμ对给定置信水平1−α1-\alpha1−α的单侧置信区间,方法与计算双侧置信区间大同小异。
计算枢轴量分布(已知σ2\sigma^2σ2为N(0,1)N(0,1)N(0,1),未知σ2\sigma^2σ2为t(n−1…
✨概率论期末速成(三套卷)——试卷①✨
✨博主:命运之光 ✨专栏:概率论期末速成(三套卷) 目录 ✨一、填空题(在下列各题填写正确答案,不填、填错,该题无分,每小题3分,共36分)✨二、计算题(本大题6小…
概率统计Python计算:经典分布的方差计算
与数学期望计算相同,scipy.stats包中提供的经典分布对象都拥有函数var,计算服从该分布的随机变量的方差。常用分布的var函数调用接口如下表所列
分布调用接口参数bernoulli(0-1分布)var( p)p:分布参数pppbinom&#x…
概率统计Python计算:学生分布分位点计算
设XXX~N(0,1)N(0,1)N(0,1),YYY~χ2(n)\chi^2(n)χ2(n),且XXX与YYY相互独立,则XY/n\frac{X}{\sqrt{Y/n}}Y/nX~t(n)t(n)t(n)。即XY/n\frac{X}{\sqrt{Y/n}}Y/nX服从自由度为nnn的学生分布,其密度函数为 h(x)Γ(n12)nπΓ(n2)…
概率统计Python计算:卡方分布分位点计算
nnn个相互独立,均服从N(0,1)N(0,1)N(0,1)的随机变量X1,X2⋯,XnX_1, X_2\cdots,X_nX1,X2⋯,Xn的平方和X12X22⋯Xn2X_1^2X_2^2\cdotsX_n^2X12X22⋯Xn2服从自由度为nnn的χ2\chi^2χ2分布,其密度函数为 f(x){12n/2Γ(n/2)xn2−1e−x2x≥00x<…
概率统计Python计算:连续型变量的独立性及约会问题解法
设(X,Y)(X, Y)(X,Y)的联合密度函数为f(x,y)f(x, y)f(x,y),联合分布函数为F(x,y)F(x, y)F(x,y),XXX和YYY的边缘密度分别为fX(x)f_X(x)fX(x)和fY(y)f_Y(y)fY(y),边缘分布函数分别为FX(x)F_X(x)FX(x)和FY(y)F_Y(y)FY(y)。我们知道&#…
概率统计Python计算:连续型随机向量边缘分布或条件分布概率计算
对于连续型随机向量(X,Y)(X,Y)(X,Y)的边缘分布和条件分布而言,密度函数都是一元函数。为计算随机变量取值落入指定区间I(a,b)I(a, b)I(a,b)的概率P(X∈I)∫abf(x)dxP(X\in I)\int_{a}^{b}f(x)dxP(X∈I)∫abf(x)dx,可以调用scipy.integrate包中的quad函…
概率统计Python计算:按条件设置随机事件
作为样本空间子集的随机事件可以由样本空间中的样本点满足一定的条件来确定。为方便应用,我们设计如下的函数来为指定样本空间设置指定条件的随机事件:
def subSet(S, condition): #设置符合条件condition的事件A set() …
概率统计Python计算:排列组合——构造样本空间
当试验的样本空间中样本点结构比较复杂时,需要仔细构造样本空间。例如,向目标射击3枪,观察每一枪是否击中目标的试验,如果将射中目标记为1,未击中目标记为0,则一个样本点可表示为一个3元组(i,j,k)(i,j,k)(i…
【概率论】连续型随机变量的分布函数及数学期望(一)
文章目录 选择题 选择题 已知F₁(x)和F₂(x)是分布函数,若 aF₁(x)-bF₂(x)也是分布函数,则下列关于常数a,b的选项中正确的是()。 A.a 3 5 \frac{3}{5} 53,b − 2 5 -\frac{2}{5} −52 B.a 2 3 \frac{2}{3} 32,b 2 3 \frac{2}{3} 32 C.a − 1 2 …
统计学_贾俊平——思考题第9章 分类数据分析
1.简述列联表的构造与列联表的分布。 答:列联表是将两个以上的变量进行交叉分类的频数分布表。 列联表的分布可以从两个方面看,一个是观察值的分布,又称为条件分布,每个具体的观察值就是条件频数;一个是期望…
概率论与数理统计(3.5) 两个随机变量函数的分布
文章目录一、离散型随机变量函数的分布1.结论2.例题二、连续性随机变量函数的分布1.ZXY例题2. ZX/Y 、ZXY例题3. Mmax{X,Y} Nmin{X,Y}例题一、离散型随机变量函数的分布
1.结论 解题思路 这也是对结论的解释。 首先确定由二维随机变量经过函数变化构造出来的新变量。 然后对应…
【SCI征稿】1区计算机算法和概率类,SCIEEI在检,CCF-C类
算法类SCI&EI
【期刊简介】IF:5.0-6.0,JCR1区,中科院3区
【检索情况】SCI&EI 双检,CCF-C类
【参考周期】走期刊部系统,3个月左右录用
【截稿日期】10篇版面
【征稿领域】概率模型、概率密度函数、模糊逻辑…
【统计学习方法】2021-10-08-统计学习方法学习记录(二)【章节一:统计学习与监督学习概论(2)】
1. 统计学习的分类:
【接上一篇文章】
1.2:按模型分类
1.2.1:概率模型与非概率模型(确定性模型) 【关于概率模型与非概率模型,可能目前的问题就是生成与判别的意义辨析;概论里追究细则意义不…
【随机数学】2021-09-15-概率统计与随机过程的学习记录与问题总结(四)(不完全是笔记)【待修改】
本来想再仔细看看但是今晚心情太差,先放上去笔记,明天早上在看吧。
【数理统计】三大抽样分布(二)
文章目录 选择题选择题 设随机变量 X ∼ N ( 0 , 1 ) , Y ∼ N ( 0 , 1 ) X\sim N(0,1),Y\sim N(0,1)
【小呆的概率论学习笔记】正态分布的代数运算
文章目录 1. 正态分布简介1. 正态分布的数字特征2. 正态分布的代数运算a. 单随机变量的代数运算b. 两个正态分布随机变量的和c. 多个正态分布随机变量的线性组合 1. 正态分布简介
正态分布应该是概率论和数理统计中最重要的一类概率分布,最早的完整论述是由数学王子…
【随机数学】2021-09-15-概率统计与随机过程的学习记录与问题总结(三)(不完全是笔记)
一
频率定义; 频率与概率关系; 有关概率的定理;(有限可加性) 公理化定义; 概率的一些性质; 加奇减偶公式;
好像没什么好说的,笔记上记了一笔我当时在写这里的题目的时候…
破圈丨2023年绿色积分消费返利:云联惠3.0升级版【循环购】商业模式
破圈丨2023年绿色积分消费返利:云联惠3.0升级版【循环购】商业模式 京东供应链商品/自营商品/供应商商品
平台上面产品超过300w款产品,均为京东供应链货品,由京东统一仓储和配送,从源头上面杜绝假冒伪劣产品的存在,然…
统计学_贾俊平——思考题第14章指数
1.什么是指数?它有哪些性质? 指数,或称统计指数,是分析社会经济现象数量变化的一种重要统计方法。它有如下一些性质: (1)相对性。指数是总体各变量在不同场合下对比形成的相对数,它可…
麦克内马尔检验(McNemar‘s Test)
麦克内马尔检验(McNemar’s Test)
配对标称数据的麦克内马尔检验(McNemar’s Test)
from mlxtend.evaluate import mcnemar
概述
McNemar的检验[1](有时也称为“受试者内卡方检验”)是对配对名义数据的统计检验。在机器学习中,我们可以使…
机器学习——Word2Vec
参考资料:
https://zhuanlan.zhihu.com/p/114538417https://www.cnblogs.com/pinard/p/7243513.html
1 背景知识
1.1 统计语言模型
统计语言模型是基于语料库构建的概率模型,用来计算一个词串 W ( w 1 , w 2 , ⋯ , w T ) W(w_1,w_2,\cdots,w_T) W…
一文了解参数检验和非参数检验
一文了解参数检验和非参数检验:
前言
假设检验
概念:是一种根据样本数据来推断总体的分布或均值、方差等总体统计参数的方法。
根据样本来推断总体的原因:
总体数据不可能全部收集到。如:质量检测问题收集到总体全部数据要耗…
置信度是干什么用的 - 通俗解释
目录1.统计是干什么用?2.举个例子3.置信度的定义1.统计是干什么用?
解释:统计是为了用测量值估计总体的 真实值;
2.举个例子
你打枪打了10次,命中了几次呢,比如平均值是8次;总体的期望&#…
概率论与数理统计之事件间的关系
1.1.3 事件间的关系
包含:A发生必导致B发生。记为:。空集包含于任何集合。相等:若,则AB并(和):A,B中至少有一个发生。记为:或交(积):A,B同时发生。记为:&…
5328笔记 Advanced ML Chapter5-Dictionary Learning and Non-negative Matrix Factorisation
求argmin||x - Dα||2 最小,本就是让Dα和x无限的逼近。当我们找到α的时候,就可以用Dα来表示x,即为将x做了矩阵分解,也就是字典学习dictionary leanring。 用NLP的word2vec来解释字典学习。D就是单词的字典,α就是检…
5003笔记 Statistic Chapter8- Feature Selection
Best subset selection:计算成本太高了、可能产生过拟合的模型 注意Forward和Backward都是考点 注意,并不是Mp模型是最好的,因为添加新的模型时候,可能不是增加模型准确率,而是降低。当出现降低的时候,我…
5003笔记 Statistic Chapter7-Missing data and class imbalance
Deterministic imputation就是回归预测,可以看出预测的点其实都在回归线上。 Random imputation也不是完全随机,而是符合原始数据的分布,或者可以理解成在回归线上加了一个error。 p0是accuracy,pe是随机分类器出的随机正…
概率论--数学期望与方差--协方差(详解)
目录
数学期望与方差
离散型随机变量的数学期望
注意
连续型随机变量的数学期望 方差 常用随机变量服从的分布 二项分布
正态分布
随机向量与随机变量的独立性
随机向量
随机变量的独立性
协方差
协方差的定义
协方差的意义
协方差矩阵 数学期望与方差
离散型随机…
5003笔记 Statistic Chapter4-High dimentional visulization and analytics
常见的聚类算法: Hierarchical, K-means, Gaussian mixture, Density 5003的K-means和5318的不同。 1)选取cluster个数K 2)给所有点随机分配不同的Kth 3)计算每个Kth中心点的位置 4)计算所有点和K个中心点的距离&am…
5328笔记 Advanced ML Chapter3-Hypothesis Complexity and Generalisation
预先定义的假设类:我们假设是最好的模型 Predefined hypothesis class 机器学习的本质就是找x到y的映射函数h。h就是我们说的模型。H就是所有映射方式的集合。 Pretrained Model都是我们认为的可能适合数据集的预定义模型,但是不一定真的适用。 矩形…
贝塔分布与狄利克雷分布
文章目录0. 补充知识0.1 贝塔函数 B(P,Q)\Beta(P, Q)B(P,Q)0.2 伽马函数 Γ(x)\Gamma(x)Γ(x)1. 贝塔分布 (Beta Distribution)1.1 概率密度函数PDF1.2 累积分布函数CDF1.3 数字特征2. 狄利克雷分布 (Dirichlet Distribution)2.1 概率密度函数PDF2.2 数字特征0. 补充知识
0.1 …
贝叶斯定理与人工智能_人工智能贝叶斯定理能力问题(MCQ)
贝叶斯定理与人工智能1) Bayesian Theorem was named after its inventor. Who invented the Bayesian theorem? Reverend Thomas BayesStuart Bayes HamiltonBayes CanneyNone of the above. Answer & Explanation Correct answer: 1Reverend Thomas Bayes Bayes’ theor…
非标准分布随机数生成 - 逆变换ITM与舍选法Rejection
统计学 - 非标准分布随机数生成
最近做了几道有关随机数生成的实验,记录下来写个总结吧,其中核心证明略。 —— 2020.3.24: 20:50
首先明白一些概念,这里随机数是指服从某种分布的随机变量,比如高斯(标准正态)分布 X…
《深度学习》数学知识基础
由于之前我学习过高等代数和解析几何,所有在此只列举不熟悉或容易忘记的知识点。目录如下: 一、 线性代数 二、概率与信息论 三、数值计算
一、线性代数
张量:一般的,一个数组中的元素分布在若干维坐标的规则网格中,…
概率论:多维随机变量
首先我们要知道,什么是多维随机变量?: 意思就是,w是样本空间里的一个事件,这个w对应着两个属性(平时都是一个w对应一个属性)这个X(w)就是一个常数,也就是概率了。 我们过去的样本空间…
联合概率和条件概率区别
为什么从定义上看,觉得联合概率和条件概率是一个意思?
P(A|B) 和 P(AB) 这俩真的不是一个东西吗??
碎碎念开始,正文请跳往第2分割线
虽然我产生了这种疑问,但我的直觉告诉我:大概是个傻逼。于…
机器学习数学基础之四多维高斯分布
多维高斯分布
概率密度函数
首先给出多维高斯分布的概率密度函数: p(x∣μ,Σ)1(2π)p2∣Σ∣12exp{−12(x−μ)TΣ−1(x−μ)}p(x|\mu,\Sigma)\frac{1}{(2\pi)^{\frac{p}{2}}|\Sigma|^{\frac{1}{2}}}exp\{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\}p(x∣μ,Σ)(…
概率统计Python计算:随机变量的线性回归
若随机向量(X,Y)(X,Y)(X,Y)存在相关系数ρXY\rho_{XY}ρXY,由 E[(Y−(aXb))2]D(Y)a2D(X)−2aCov(Y,X)(E(Y)−aE(X)−b)2D(Y)(1−ρXY2)D(X)(a−ρXYD(Y)D(X))2(E(Y)−aE(X)−b)2E[(Y-(aXb))^2]D(Y)a^2D(X)-2a\text{Cov}(Y, X)(E(Y)-aE(X)-b)^2\\ D(Y)(1-\rho_{XY}…
概率统计Python计算:解古典概型问题
假定以SSS为样本空间的随机试验是一个等概模型,事件A⊆SA\subseteq SA⊆S。若能算得∣S∣n|S|n∣S∣n,∣A∣m|A|m∣A∣m,我们知道P(A)m/nP(A)m/nP(A)m/n。我们把这样的计算方法定义成下列的Python函数。
from sympy import Rational #导入R…
概率统计Python计算:随机事件的Python表示
随机试验有确定的样本空间,样本空间是试验的所有样本点的集合,随机事件是样本空间的子集合。所以,要在计算机上表示随机试验和随机事件,应能表示集合。Python 为我们提供了一个表示集合的数据结构set。这个set 类的对象和数学中的…
82、美团算法题---最长回文子串
最长回文子串 力扣
一、题目
给你一个字符串 s,找到 s 中最长的回文子串。 二、思路
我们知道回文串一定是对称的,所以我们可以每次循环选择一个中心,进行左右扩展,判断左右字符是否相等即可。
由于存在奇数的字符串和偶数的字…
81、美团算法题---最小路径和(动态规划)
一、题目
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。 二、思路 三、实现
/*** param {number[][]} grid* return {number}*/
var min…
微积分中计算椭圆面积的几种方法
Find the area enclosed by the ellipse x2a2y2b21\frac{x^2}{a^2}\frac{y^2}{b^2}1a2x2b2y21 Trigonometric Substitutions yb1−x2a2yb \sqrt[]{1-\frac{x^2}{a^2}}yb1−a2x2 let xasinθxa\sin\thetaxasinθ then ybcosθyb\cos\thetaybcosθ , dxacosθdθdx…
markdown 数学公式Latex语法
在输入数学公式的时候,需要在数学公式的前后加入$符号,将需要输入的公式加入到$中间。
行内公式
$行内公式$行间公式
?
行间公式
?角标(上下标)
上标 ^下标 _
名称数学表达式markdown公式上标aba^bab$a^b$下标aba_bab$a_…
圆周上任意取三点组成直角三角形的概率为0
圆周上任意取三点组成直角三角形的概率为0!不失一般性,我们在一个单位圆上做分割,下图中两点之间的弧长用对应的字母表示: 这时,根据圆周角与所夹弧长的关系可以把该问题转化为几何概型:
三角形为锐角三角…
关于语言模型中的平滑
在语言模型计算概率的时候,我们会碰到概率为0的情况,即计算的单词在语言模型中并没有出现过。这个时候会使用平滑的方法计算概率,一般分为以下几种:
Add-One Smoothing
Add-K Smoothing
其中Add-One Smoothing可以看作Add-K Sm…
三门问题(一个有趣的概率题)
::: CJK UTF8gbsn
三门问题是一个十分有趣的问题。 它讲述的是这样一个问题。 假如有一档节目。 节目里面有设置有三道门, 其中一道门里面有奖品。 主持人会让你选一道门。当你做出选择之后, 主持人会将你没有选择的两扇门中选择一个空门打开࿰…
数学分析第七课(复数)
The Complex Field. We firstly introduce the definition of complex numbers.
Definiton: A complex numbers is an ordered pair (a,b)(a,b)(a,b) of real numbers. (a,b)(a,b)(a,b) and (b,a)(b,a)(b,a) are regarded as distinct if a≠ba\ne bab. Let x(a,b),y(c,d)…
数学分析第六课(域以及域的性质)
In this lecture, we shall introduce an important concept which is called field.
Definition: A field is a set FFF with two operations, called addtion and multiplication, which satisfy the following so-called field axionms. Axioms for addition ∀x,y(x,y∈F)…
回溯法——总结(是否包含重复元素,是否全排列)
回溯法 主要要考虑三种情况:
如果是输出的是全排列,即元素顺序不一样,也属于不一样的结果: 设置循环: for (int i 0; i < nums.length; i) ,不需要记录当前下标,例如:idx&#…
P2801 教主的魔法 —— 分块+sort+暴力
P2801 教主的魔法 写分块的时候一定要注意什么时候用l, r 什么时候用bel[x],bel[y],一不注意就容易出错 // Decline is inevitable,
// Romance will last forever.
#include <bits/stdc.h>
using namespace std;
#define mst(a, x) memset(a, x…
朴素贝叶斯(Naive Bayes)
目录
1 概念
1.1 概率论基础
1.2 贝叶斯公式
1.3 朴素贝叶斯分类器
2 算法的优缺点
3 MATLAB代码
参考文献 1 概念
1.1 概率论基础
(1)条件概率公式
设A,B是两个事件,且P(A)>0,P(B)>0,由图1可知,在事件…
【考研数学】概率论与梳理统计 | 第一章——随机事件与概率(1)
文章目录 一、随机试验与随机事件1.1 随机试验1.2 样本空间1.3 随机事件 二、事件的运算与关系2.1 事件的运算2.2 事件的关系2.3 事件运算的性质 三、概率的公理化定义与概率的基本性质3.1 概率的公理化定义3.2 概率的基本性质 写在最后 一、随机试验与随机事件
1.1 随机试验 …
统计动力学笔记(一)动态系统随机信号在时域中的变换(自留用)
动态系统随机信号在时域中的变换 1. 系统工作质量的表征及若干统计学概念2. 各态遍历性3. 相关函数的性质4. 确定相关函数的实验方法5. 通过线性动态系统的静定随机信号的特性6. 系统输出的均方误差计算 1. 系统工作质量的表征及若干统计学概念
设一个动态系统的输入为 u ( t …
朴素贝叶斯==基于样本特征来预测样本属于的类别y
目录
朴素贝叶斯基于样本特征来预测样本属于的类别y
朴素贝叶斯算法的基本概念与核心思想 假设两个特征维度之间是相互独立的
拉普拉斯平滑增加出现次数保证0不出现
编辑 基于样本特征来预测样本属于的类别y
什么是拉普拉斯平滑 朴素贝叶斯基于样本特征来预测样本属于的…
Thanos and Avengers playing roulette
Today I found an interesting revision of Avengers: Endgame. It says: 初代复仇者六人组,每人带一宝石手套,去找灭霸决战,到了草屋,七人围圈而坐,六对一,互相打响指意图消灭对方。灭霸人少,给…
Python快速检验数据分布
假设检验的前提是确定数据的分布,本文介绍Python检验数据样本是否服从一定分布。使用方法是柯尔莫可洛夫-斯米洛夫检验(Kolmogorov–Smirnov test,K-S test),K-S检验方法适用于探索连续型随机变量的分布,对…
蒙特卡洛量化分析方法
蒙特卡洛方法主要思想:对于一个随机系统,输出随输入变化是随机的,那么通过重复采样的方法可以得到输出的具体分布,进而再对输出分布形式进行分析。
大数定律:当在试验不变的条件下,重复试验多次࿰…
运用谱分解定理反求实对称矩阵
文章目录 谱分解定理定理的运用 谱分解定理
设三阶实对称矩阵 A A A,若矩阵 A A A 的特征值为 λ 1 , λ 2 , λ 3 \lambda_1,\lambda_2,\lambda_3 λ1,λ2,λ3,对应的特征向量分别为 α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α1,α…
概率论好题:洛谷P5389 [Cnoi2019]数学课
题目大意
给定一个序列 aaa ,满足 an123...na_{n}123...nan123...n,根据题目给定的概率选择其中两个(可相同)的元素 v1,v2v1,v2v1,v2 ,我们记录 a∈[1...v1]a \in [1...v1]a∈[1...v1],b∈[1...v2]b \in…
每周学点数学 2:概率论基础1
泊松分布、正态分布、二项分布 文章目录 1.概率论学习中的重难点2.主要工具介绍1. Python2. MATLAB3. R4. Octave5. Microsoft Excel6. 统计软件 3.理论内容概览(前两点)1. 概率2. 概率分布 注:本文适用于在在数学建模的应用中,回…
如何深刻理解从二项式分布到泊松分布
泊松镇贴
二项分布和泊松分布的表达式
二项分布: P ( x k ) C n k p k ( 1 − p ) n − k P(xk) C_n^kp^k(1-p)^{n-k} P(xk)Cnkpk(1−p)n−k
泊松分布: P ( x k ) λ k k ! e − λ P(xk) \frac{\lambda^k}{k!}e^{-\lambda} P(xk)k!λke−…
业余爱好-生物信息学/生物化学/物理/统计学/政治/数学/概率论/AI/AGI/区块链
生物信息学 高等数学—元素和极限-实数的定义高等数学—元素和极限-实数的元素个数高等数学—元素和极限-自然数个数少于实数个数高等数学—元素和极限-无穷大之比较高等数学—元素和极限-级数的收敛高等数学—元素和极限-极限的定义数学分析与概率论人工智能AI数学基础——全套…
【深度学习】概率图模型(一)概率图模型理论简介
文章目录 一、概率图模型1. 联合概率表2. 条件独立性假设3. 三个基本问题 二、模型表示1. 有向图模型(贝叶斯网络)2. 无向图模型(马尔可夫网络) 三、学习四、推断 概率图模型(Probabilistic Graphical Model࿰…
【线性代数与矩阵论】矩阵的谱半径与条件数
矩阵的谱半径与条件数
2023年11月18日 文章目录 矩阵的谱半径与条件数1. 矩阵的谱半径2. 谱半径与范数的关系3. 矩阵的条件数下链 1. 矩阵的谱半径
定义 设 A ∈ C n n {A\in \mathbb C^{n \times n} } A∈Cnn , λ 1 , λ 2 , ⋯ , λ n { \lambda_1,\lambda_2…
链式法则(Chain Rule)
定义
链式法则(Chain Rule)是概率论和统计学中的一个基本原理,用于计算联合概率分布或条件概率分布的乘积。它可以用于分解一个复杂的概率分布为多个较简单的条件概率分布的乘积,从而简化概率分析问题。
链式法则有两种常见的形…
决策树算法——C4.5算法
目录
1.ID3算法
2.C4.5算法
3.信息增益率
(1)信息增益率
(2)案例
4.决策树的剪枝
5.总结
(1)优点与改进
(2)缺点
(3) 总结及展望 近年来决策树方…
【论文笔记】A theory of learning from different domains
防盗 https://www.cnblogs.com/setdong/p/17756127.html domain adaptation 领域理论方向的重要论文. 这篇笔记主要是推导文章中的定理, 还有分析定理的直观解释. 笔记中的章节号与论文中的保持一致.
1. Introduction
domain adaptation 的设定介绍: 有两个域, source domain…
汤姆·齐格弗里德《纳什均衡与博弈论》笔记(7)博弈论与概率论
第十一章 帕斯卡的赌注——博弈、概率、信息与无知 在与费马就这个问题的通信过程中,帕斯卡创造出了概率论。另外,帕斯卡在进行严谨的宗教反思中,得出了概率这个概念,它在此几百年后,成为一个关键的、对博弈论的提出有…
概率论第二章作业题-3.27
计算概率分布的时候,以第四题为例,假设我们第二次命中,那么该事件发生的前提是第一次没有命中
计算概率分布的时候把每一个概率计算出来,最后用一个表格罗列所有情况即可
像第八题一样是二项分布,把公式套进去计算即…
python计算概率分布
目录 1、泊松分布
2、卡方分布
3、正态分布
4、t分布
5、F分布 1、泊松分布
泊松分布是一种离散概率分布,描述了在固定时间或空间范围内,某个事件发生的次数的概率分布。该分布以法国数学家西蒙德尼泊松的名字命名,他在19世纪早期对这种…
26版SPSS操作教程(初级第十四章)
前言
#由于导师最近布置了学习SPSS这款软件的任务,因此想来平台和大家一起交流下学习经验,这期推送内容接上一次第十三章的学习笔记,希望能得到一些指正和帮助~
粉丝及官方意见说明
#针对官方爸爸的意见说的推送缺乏操作过程的数据案例文件…
概率论中的全概率公式、贝叶斯公式解析
全概率公式
定义 全概率公式是用来计算一个事件的概率,这个事件可以通过几个互斥事件的并集来表示。这几个互斥事件称为“完备事件系”。实质是由原因推结果。
公式 用途 全概率公式通常用于计算一个事件的总概率,特别是当这个事件与几个不同的因素相关…
概率论中,相关性和独立性的关系
相关性和独立性是概率统计中两个关键的概念。 相关性(Correlation): 定义: 相关性衡量两个变量之间的线性关系程度。如果两个变量的值在某种趋势下同时变化,我们说它们是相关的。相关性的取值范围在 -1 到 1 之间&…
蒙特霍尔问题(选择三扇门后的车与羊)及其贝叶斯定理数学解释
1. 蒙特霍尔问题
有一个美国电视游戏节目叫做“Let’s Make a Deal”,游戏中参赛者将面对3扇关闭的门,其中一扇门背后有一辆汽车,另外两扇门后是山羊,参赛者如果能猜中哪一扇门后是汽车,就可以得到它。
通常…
【RL】Bellman Equation (贝尔曼等式)
Lecture2: Bellman Equation
State value
考虑grid-world的单步过程: S t → A t R t 1 , S t 1 S_t \xrightarrow[]{A_t} R_{t 1}, S_{t 1} StAt Rt1,St1 t t t, t 1 t 1 t1:时间戳 S t S_t St:时间 t t t时所处的sta…
离散型概率密度函数的分布列⇔分布函数
目录
一、super误区
1.分布函数的定义
二、分布列⇒分布函数
二、分布列⇐分布函数 一、super误区
我在读定义的时候陷入了一个误区,与大家分享一下。
1.分布函数的定义 由于是离散型的概率密度函数,我把他抽象到数轴上理解:
如下分布…
python 实现 AIGC 大模型中的概率论:生日问题的公式推导
在前两节中,我们推导了生日问题的求解算法,但在数学上的最终目标就是希望能针对问题推导出一个简洁漂亮的公式,就像爱因斯坦著名的质能方程 E MC^2 那样,毕竟数学是以符号逻辑来看待世界本质的语言,所以絮絮叨叨不是数…
利用条件概率进行事件预测与分析
条件概率是概率论中的重要概念,它描述了在已知某一事件发生的条件下,另一事件发生的概率。利用条件概率进行事件的预测与分析在各个领域中都有着重要的应用,包括金融、医学、工程、社会科学等。本文将探讨条件概率的定义、性质以及它在现实生…
朴素贝叶斯(NBM,Naive Bayesian Model), NB 算法 简介
朴素贝叶斯(NBM,Naive Bayesian Model), NB 算法
分类算法
在贝叶斯原理的基础上,预先假定了特征与特征之间的相互独立。
贝叶斯的原理:当不知道这个事物实际情况的时候,我们可以根据一些相关的条件来判…
机器学习之朴素贝叶斯(Naive Bayes)附代码
概念
朴素贝叶斯(Naive Bayes)是一种基于贝叶斯定理的机器学习算法,它被广泛用于分类和文本分析任务。该算法的"朴素"体现在对特征之间的条件独立性的假设,即给定类别,特征之间是相互独立的。尽管这个假设在实际情况中并不总是成立,但这种简化有助于降低计算复…
概率中的 50 个具有挑战性的问题 [05/50]:正方形硬币
一、说明 我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克莫斯特勒(Frederick Mosteller)的《概率论中的五十个具有挑战性的问题与解决方案》)一书。我认为创建一个系列来讨论这些可能作为面试问题出现的迷人问题会很有趣。每篇…
Full-RNS CKKS
参考文献:
[HS13] Halevi S, Shoup V. Design and implementation of a homomorphic-encryption library[J]. IBM Research (Manuscript), 2013, 6(12-15): 8-36.[BEHZ16] Bajard J C, Eynard J, Hasan M A, et al. A full RNS variant of FV like somewhat homomo…
python统计学卡方,t,F分布
卡方分布(Chi-square distribution)是一种常见的概率分布,通常用于统计推断和假设检验中。它是通过将标准正态分布的平方和进行自由度调整而得到的。卡方分布的自由度决定了分布的形状。t分布(Students t-distribution)…
【小白学机器学习5】MSE, RMSE,MAE, MAPE, WMAPE
目录
1 评价误差的各种度量指标
2 从误差的评价开始捋这个问题
2.1 误差问题的由来:回归模型预测值和真实值的差距
2.2 如何评价某函数的预测值是否足够好? 如何比较不同的预测函数的预测值的好坏呢?
2.3 最小二乘法:应该叫最…
泊松分布与二项分布的可加性
泊松分布与二项分布的可加性
泊松分布的可加性 例 : 设 X , Y X,Y X,Y 相互独立 , X ∼ P ( λ 1 ) X\sim P(\lambda_1) X∼P(λ1) , Y ∼ P ( λ 2 ) Y\sim P(\lambda_2) Y∼P(λ2) , 求证 Z X Y ZXY ZXY 服从参数为 λ 1 λ 2 \lambda_1 \lambda_2 λ1λ2 …
[数理统计]中国科技技术大学缪柏其
中国科学技术大学 数理统计 缪柏其
笔记正在不断完善中,博主还有其他上万字精品笔记 编辑P10 前言1-统计思想 41:33 介绍了数理统计的重要性和应用领域。主讲人强调了统计学与数学的区别,指出统计学是以数据为研究对象的一门科学,强调了统计思想的重…
Excel·VBA二维数组组合函数的应用实例之概率计算
看到一个视频《李永乐老师的抖音 - 骰子概率问题》,计算投出6个骰子恰好出现1、2、3、4、5、6这6个点数的概率
李永乐老师的计算方法是,第1个概率为1即6/6,第2个不与之前相同的概率为5/6,第3个同理概率为4/6,因此该问…
第二部分 离散型随机变量
目录 求分布律里的未知数 例1 例2 根据X的分布律写Y的分布律 例3 根据(X,Y)的分布律写Z的分布律 例4 根据(X,Y)的分布律写边缘分布律 例5 X与Y相互独立时的联合分布律 例6 根据分布律求期望、方差 例7 求分布律里的未知数 例1 已知X的分布律为 X-202P0.40.3k ,试求k 解 0.40…
概率图模型--贝叶斯网络
概率图模型–贝叶斯网络 – 潘登同学的Machine Learning笔记 文章目录概率图模型--贝叶斯网络 -- 潘登同学的Machine Learning笔记概率图模型什么是概率图概率图模型的三要素--表示、推理、学习概率图模型的表示概率图模型的推理概率图模型的学习三者的联系贝叶斯网络朴素贝叶斯…
技术学习|CDA level I 描述性统计分析(常用的数据分布)
推断性统计分析方法的基础理论——常用的分布(两点分布、二项分布、正态分布[含标准正态分布]、χ2分布、t分布、F分布。
随机试验:结果不确定的实验,例如,进行一次抛硬币实验,结果是不确定的。对于随机试验的结果&am…
【机器学习前置知识】共轭分布
贝叶斯概率公式的组成
贝叶斯定理的概率公式: P ( θ ∣ X ) P ( X ∣ θ ) P ( θ ) P ( X ) P(θ|X){P(X|θ)P(θ)\over{P(X)}} P(θ∣X)P(X)P(X∣θ)P(θ) 先验分布 P ( θ ) P(θ) P(θ) :参数的先验分布是指在观测到新的数据之前,根…
excel统计分析——两因素无重复方差分析
参考资料:生物统计学 从严格意义上讲,两因素试验都应当设置重复观测值,以便检验交互作用是否真实存在,对试验误差有更准确的估计,从而提高检验效率。但根据专业知识或先前的试验已经证明两个因素不存在交互作用时&…
python实现常见一元随机变量的概率分布
一. 随机变量
随机变量是一个从样本空间 Ω \Omega Ω到实数空间 R R R的函数,比如随机变量 X X X可以表示投骰子的点数。随机变量一般可以分为两类:
离散型随机变量:随机变量的取值为有限个。连续型随机变量:随机变量的取值是连…
概率密度函数及其在信号方面的简单理解(上)概率密度函数
概率密度函数及其在信号方面的简单理解(上)概率密度函数 上篇 概率密度函数1 离散随机变量与连续型随机变量2 离散随机变量的分布函数2.1 概率函数2.2 概率分布2.3 概率分布函数(累积分布函数!) 3 连续型随机变量的概率…
检测概率与目标状态相关时的PHD滤波器
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1. 影响目标状态相关检测概率的因素2. 更新步骤的修改2.1 权重更新公式2.2 权重的归一化 3. 应用实例——相控阵雷达多目标跟踪3.1 问题建模3.2 实现方法 4. 结语 声…
概率基础——极大似然估计
概率基础——极大似然估计
引言
极大似然估计(Maximum Likelihood Estimation,简称MLE)是统计学中最常用的参数估计方法之一,它通过最大化样本的似然函数来估计参数值,以使得样本出现的概率最大化。极大似然估计在各…
【算法小记】——机器学习中的概率论和线性代数,附线性回归matlab例程
内容包含笔者个人理解,如果错误欢迎评论私信告诉我 线性回归matlab部分参考了up主DR_CAN博士的课程 机器学习与概率论
在回归拟合数据时,根据拟合对象,可以把分类问题视为一种简答的逻辑回归。在逻辑回归中算法不去拟合一段数据而是判断输入…
简单随机抽样之区间估计
中心极限定理
中心极限定理(CLT):求独立随机变量的近似的和的分布,它近似服从正态分布例如:当n趋于无穷时,可以用正态分布去近似二项分布 设 Φ ( x ) 为 N ( 0 , 1 ) 的分布函数,对一切的 − …
5328笔记 Advanced ML Chapter7-Learning with Noisy Data
第二行,最左边第一张图是高斯噪点,第二张是椒盐噪点,第三张是块噪点block noise。 下边右边,是由于人的动作因素或者眼睛等环境因素,造成的噪点。 Large noise是outlier,它们的数据和我们的数据本身分布已…
5003笔记 Statistic Chapter3-Density Estimation
Density Estimation:密度估计 Cumulative distribution:累计分布函数F(x) 注意,均值mean E(x) np, Var(x) np(1-p) Continuous distribution:连续分布 连续的边界不重要,离散的边界重要 这里连续变量的PD…
ppt学习日记:L4-图片实战技巧
目录
一、图片的两个作用
1.1 佐证事实
1.2 烘托气氛
二、如何找好看的图片
2.1 3W联想法
2.2 三位老师换词法
三、挑选图片的三张网
3.1 符合主题
3.2 符合气质
3.3 高清留白
四、图片的5种设计方法
4.1 为图片增加渐变蒙版
4.2 墨迹效果
4.3 布尔运算
4.4 …
马尔可夫预测(Python)
马尔科夫链(Markov Chains)
从一个例子入手:假设某餐厅有A,B,C三种套餐供应,每天只会是这三种中的一种,而具体是哪一种,仅取决于昨天供应的哪一种,换言之&#…
【机器学习】【概率论】【损失熵】【KL散度】信息量、香农熵和KL散度的计算
1、信息量(Amount of Information)
对于一个事件: 小概率 --> 大信息量 大概率 --> 小信息量 独立事件的信息量可以相加 I ( x ) l o g 2 ( 1 p ( x ) ) − l o g 2 ( p ( x ) ) I(x)log_2(\frac{1}{p(x)})-log_2(p(x)) I(x)log2…
蒙特卡洛原理及实例(附Matlab代码)
文章目录一、理论基础1.1 伯努利大数定理1.2 辛钦大数定理1.3 切比雪夫大数定理1.4 三者区别和联系二、蒙特卡洛法2.1 蒙特卡洛的起源2.2 蒙特卡洛的解题思路2.2 蒙特卡洛法的应用三、几个小栗子3.1 求解定积分3.1.1 解析法3.1.2 蒙特卡洛法3.2 求解六边形面积3.2.1 解析法3.2.…
【概率论】关于为什么样本标准偏差分母是n-1的进一步理解
上接物理实验引发的思考:总体标准偏差和样本标准偏差的区别是什么?标准偏差和标准误的区别是什么?,现在系统地学了概率论与数理统计,有了新的理解。 首先我们再回顾一些概念。设总体为XXX,样本为X1,X2,⋯,X…
概率统计Python计算:单因素试验总偏差平方和的分解
单因素试验模型XXX是一个数组的数组:X{X1,X2,⋯,Xs}X\{X_1,X_2,\cdots,X_s\}X{X1,X2,⋯,Xs},其中Xi{Xi1,Xi2,⋯,Xini}X_i\{X_{i1},X_{i2},\cdots,X_{in_i}\}Xi{Xi1,Xi2,⋯,Xini},i1,2⋯,si1,2\cdots,si1,2⋯,s(诸…
概率统计Python计算:双正态总体未知总体方差总体均值差双侧假设的T检验
对两个独立正态总体XXX~N(μ1,σ2)N(\mu_1,\sigma^2)N(μ1,σ2)及YYY~N(μ2,σ2)N(\mu_2,\sigma^2)N(μ2,σ2),其中σ2\sigma^2σ2未知而要对双侧假设H0:μ1−μ2δ,H1:μ1−μ2̸δH_0:\mu_1-\mu_2\delta,H_1:\mu_1-\mu_2\not\deltaH0:μ1−μ2δ,H1:μ…
概率统计Python计算:双正态总体已知总体方差总体均值差单侧假设的Z检验
设XXX和YYY相互独立且XXX~N(μ1,σ12)N(\mu_1,\sigma_1^2)N(μ1,σ12),YYY~N(μ2,σ22)N(\mu_2,\sigma_2^2)N(μ2,σ22),其中σ12\sigma_1^2σ12和σ22\sigma_2^2σ22是已知的。来自XXX和YYY的容量分别为n1n_1n1和n2n_2n2的样本均值为X‾…
概率统计Python计算:单个正态总体均值单侧假设的Z检验
对正态总体参数的单侧假设检验,可以用如下的p值法进行。设显著水平为α\alphaα,考虑假设H0H_0H0的右侧检验。首先,注意到检验统计量的分布对应显著水平α\alphaα的右分位点bbb,实际上就是其残存函数S(x)S(x)S(x)(1…
概率统计Python计算:单个正态总体方差的双侧区间估计
计算指定置信水平下正态总体方差σ2\sigma^2σ2的置信区间,涉及样本方差s2s^2s2,样本容量nnn和置信水平1−α1-\alpha1−α等三个因素。计算步骤为
计算χ2(n−1)\chi^2(n-1)χ2(n−1)分布概率为1−α1-\alpha1−α的双侧分位点aaa和bbb;计算…
概率统计Python计算:连续型总体未知参数的最大似然估计
设(X1,X2,⋯,Xn)(X_1,X_2,\cdots,X_n)(X1,X2,⋯,Xn)是来自总体XXX的样本,(x1,x2,⋯,xn)(x_1,x_2,\cdots,x_n)(x1,x2,⋯,xn)为样本的一个观测值。已知XXX的分布,其中含有mmm个未知参数θ1,θ2,⋯,θm\theta_1,\theta_2,\cdots,\theta_mθ1,…
概率统计Python计算:总体未知参数的矩估计
设样本(X1,X2,⋯,Xn)(X_1,X_2,\cdots,X_n)(X1,X2,⋯,Xn)来自XXX,XXX的分布中含有mmm个未知参数θ1,θ2,⋯,θm\theta_1,\theta_2,\cdots,\theta_mθ1,θ2,⋯,θm。设XXX存在直到mmm阶的原点矩E(X),E(X2),⋯,E(Xm)E(X),E(X^2),\cdots,E(X^m)E(X),E(X2),⋯…
概率统计Python计算:样本数据的经验分布函数
设(x1,x2,⋯,xn)(x_1,x_2,\cdots,x_n)(x1,x2,⋯,xn)是总体XXX的一个样本观测值。与绘制直方图相仿,记amin{x1,x2,⋯,xn}amin\{x_1,x_2,\cdots,x_n\}amin{x1,x2,⋯,xn},bmax{x1,x2,⋯,xn}bmax\{x_1,x_2,\cdots,x_n\}bmax{x1,x2,⋯,xn}。…
概率统计Python计算:中心极限定理的验证
中心极限定理告诉我们,独立同分布的随机变量序列X1,X2,⋯,Xn,⋯X_1,X_2,\cdots,X_n,\cdotsX1,X2,⋯,Xn,⋯,若E(Xi)μE(X_i)\muE(Xi)μ,D(Xi)σ2D(X_i)\sigma^2D(Xi)σ2,i1,2,⋯i1,2,\cdotsi1,2,⋯。则 limn→∞P(∣∑…
概率统计Python计算:F分布分位点计算
设XXX,YYY相互独立,且分别服从χ2(m)\chi^2(m)χ2(m)和χ2(n)\chi^2(n)χ2(n),则XY\frac{X}{Y}YX~F(m−1,n−1)F(m-1, n-1)F(m−1,n−1),即XY\frac{X}{Y}YX服从自由度为mmm和nnn的FFF分布。服从F(m−1,n−1)F(m-1, n-1)F(m−1…
概率论与数理统计(3.1)二维随机变量
二维随机变量1.二维随机变量的定义2.二维随机变量分布函数(联合分布函数)的定义3.分布函数F(x,y)的基本性质(4条)4.二维离散型随机变量1).定义2).二维离散型随机变量的分布律3).二维离散型随机变量的分布函数4).二维离散型随机变量分布律和分布函数求解例…
机器学习_15_贝叶斯算法
文章目录 1 贝叶斯定理相关公式2 朴素贝叶斯算法2.1 朴素贝叶斯算法推导2.2 朴素贝叶斯算法流程 3 高斯朴素贝叶斯4 伯努利朴素贝叶斯5 多项式朴素贝叶斯6 贝叶斯网络6.1 最简单的一个贝叶斯网络6.2 全连接贝叶斯网络6.3 “正常”贝叶斯网络6.4 实际贝叶斯网络:判断…
人工智能之大数定理和中心极限定理
大数定律
大数定律:是一种描述当试验次数很大时所呈现的概率性致的定律,由概率统计定义“频率收敛于概率”引申而来。换而言之,就是n个独立分布的随机变量其观察值的均值依概率收敛于这些随机变量所属分布的理论均值,也就是总体均…
《统计学简易速速上手小册》第9章:统计学在现代科技中的应用(2024 最新版)
文章目录 9.1 统计学与大数据9.1.1 基础知识9.1.2 主要案例:社交媒体情感分析9.1.3 拓展案例 1:电商销售预测9.1.4 拓展案例 2:实时交通流量分析 9.2 统计学在机器学习和人工智能中的应用9.2.1 基础知识9.2.2 主要案例:预测客户流…
《统计学简易速速上手小册》第10章:案例研究和未来趋势(2024 最新版)
文章目录 10.1 统计学成功案例分析10.1.1 基础知识10.1.2 主要案例:药物临床试验10.1.3 拓展案例 1:市场趋势分析10.1.4 拓展案例 2:社会行为研究 10.2 统计学的伦理考量10.2.1 基础知识10.2.2 主要案例:个性化医疗研究10.2.3 拓展…
【深度学习】S2 数学基础 P4 概率论
目录 基本概率论概率论公理随机变量 处理多个随机变量联合概率条件概率贝叶斯定理边际化独立性应用 期望与方差 未完待续
基本概率论
概率论公理
随机变量
处理多个随机变量
联合概率
条件概率
贝叶斯定理
边际化
独立性
应用
期望与方差
伯努利分布、二项分布、概念辨析
伯努利分布
伯努利分布是二项分布的一种特殊情况,它描述的是单次随机试验中,只有两种结果的概率分布。其中,一种结果的概率为 ppp,另外一种结果的概率为 1−p1-p1−p。伯努利分布的概率质量函数如下: f(k;p){pif k1,1…
Huggingface的GenerationConfig 中的top_k与top_p详细解读
Huggingface的GenerationConfig 中的top_k与top_p详细解读 Top_kTop_p联合共用 Top_k
top-k是指只保留概率最高的前k个单词,然后基于剩余单词的概率进行归一化,从中随机抽取一个单词作为最终输出。这种方法可以限制输出序列的长度,并仍然保持…
两个高斯分布之间的KL散度
一元高斯分布的概率分布函数为 f ( x ) 1 2 π σ e − ( x − μ ) 2 2 σ 2 . (1.1) f\left( x \right) \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}}}.\tag{1.1} f(x)2π σ1e−2σ2(x−μ)2.(1.1)
给定两…
【感知算法】Dempster-Shafer理论(上)
Dempster-Shafer理论
三个概念Mass Belief Plausibility 一个论断的置信度,表达为一个区间,上下界为plausibility\belief, b e l i e f < p l a u s i b i l i t y belief < plausibility belief<plausibility. mass是各个论断子集…
假设检验/T检验/F检验/Z检验/卡方检验
****显著性水平: 一个概率值,原假设为真时,拒绝原假设的概率,表示为 alpha 常用取值为0.01, 0.05, 0.10
****什么是P值? p值是当原假设为真时样本观察结果及更极端结果出现的概率。 如果P值很小,说明这种情…
机器学习系列-生成模型和判别模型
文章目录 前言1.生成模型和判别模型2.常见的生成模型和判别模型3.判别式模型和生成式模型的优缺点 前言
监督学习模型可以分为生成模型(generative model)和判别模型(discriminative model)
1.生成模型和判别模型
判别模型由数据直接学习决策函数 f ( x ) f(x) f(x)或者条件…
充分统计量和因子分解定理
充分统计量 定义: 设样本 X X X的服从分布 f ( X ∣ θ ) f(X|\theta) f(X∣θ), θ ∈ Θ \theta\in\Theta θ∈Θ,设 T T ( X ) TT(X) TT(X)为一统计量,若在已知 T T T的条件下,样本 X X X的条件分布与参数 θ \the…
高数考研 -- 公式总结(更新中)
1. 两个重要极限
(1) lim x → 0 sin x x 1 \lim _{x \rightarrow 0} \frac{\sin x}{x}1 limx→0xsinx1, 推广形式 lim f ( x ) → 0 sin f ( x ) f ( x ) 1 \lim _{f(x) \rightarrow 0} \frac{\sin f(x)}{f(x)}1 limf(x)→0f(x)sinf(x)1. (2) lim …
Jensen‘s inequality(詹森不等式)
Jensen’s inequality(詹森不等式)是数学中的一条重要不等式,由丹麦数学家Johan Jensen于1906年提出。它是凸分析和概率论中的一个基本工具,对于理解和证明许多理论概念如期望值、方差、熵以及各种不等式都具有重要作用。 Jensen’…
25高数考研张宇 -- 公式总结(更新中)
1. 两个重要极限
(1) lim x → 0 sin x x 1 \lim _{x \rightarrow 0} \frac{\sin x}{x}1 limx→0xsinx1, 推广形式 lim f ( x ) → 0 sin f ( x ) f ( x ) 1 \lim _{f(x) \rightarrow 0} \frac{\sin f(x)}{f(x)}1 limf(x)→0f(x)sinf(x)1. (2) lim …
概率论与数理统计 P6 条件概率
文章目录 P6 条件概率一.条件概率二.乘法定理三.全概率公式 & 贝叶斯公式3.1 全概率公式(由因求果)3.2 贝叶斯公式(由果导因) P6 条件概率
一.条件概率
1.Def:设A、B是两个事件,且 P ( A ) > 0 P(…
概率论与数理统计(随机事件与概率)
1随机事件与概率
1.1随机事件及其运算规律
1.1.1运算
交换律结合律分配律德摩根律
1.2概率的定义及其确定方法
1.2.1概率的统计定义
频率 设在 n 次试验中,事件 A 发生了(A)次,则称为事件 A 发生的频率。
1.2.2概率的统计定义
在一组恒定不变的条…
贝叶斯定理,先验信念,似然,后验概率
贝叶斯定理形式如下: P ( H ∣ D ) P ( H ) ⋅ P ( D ∣ H ) P ( D ) P(H|D) \frac{P(H) \cdot P(D|H)}{P(D)} P(H∣D)P(D)P(H)⋅P(D∣H)
回顾一下,这个公式包含 3 个有特殊名称的要素: P ( H ∣ D ) P(H|D) P(H∣D) 是后验概率…
贝叶斯定理(Bayes‘ rule)
bayes’ rule本质上是在讲什么
贝叶斯定理(Bayes’ rule)是概率论中的一个基本定理,它描述了在获得新证据后更新先验概率的过程。该定理以托马斯贝叶斯(Thomas Bayes)的名字命名,尽管他并没有以公式的形式…
【状态估计】概率论基础
《机器人学的状态估计》是入行SLAM的经典书籍之一,其中有大量的公式相关的内容,看起来还是比较艰涩的。最近重新读一遍,顺便将其中的一些内容记录下来,方便以后回看。 概率密度函数
定义
定义 x x x为区间 [ a . b ] [a.b] [a.b…
概率论与数理统计 Chapter3. 随机变量的数字特征
概率论与数理统计 Chapter3. 随机变量的数字特征 1. 重要定义 & 定理 1. 数学期望(均值) 1. 定义2. 性质 2. 中位数3. 方差 & 标准差 1. 定义2. 性质 4. 协方差 & 相关系数 1. 协方差2. 相关系数 5. 大数定理 1. 大数定理2. 马尔可夫不等式3…
概率论与数理统计 Chapter2. 随机变量及概率分布
概率论与数理统计 Chapter2. 随机变量及概率分布 1. 离散分布 1. 二项分布 1. 概率密度函数2. 典型应用场景 2. 负二项分布(帕斯卡分布) 1. 概率密度函数2. 典型应用场景 3. 多项分布 1. 概率密度函数2. 典型应用场景 4. 超几何分布 1. 概率密度函数2. 典…
概率论与数理统计——事件间的关系
包含
事件A发生必然导致事件B发生。 代数中经常用这种方法证明两个事件相等。
事件的并(和)
A与B至少有一个发生
事件的交(积)
A与B同时发生 无限可列个:能按某种规律能把他排成一个序列(实变函数…
CRPS:贝叶斯机器学习模型的评分函数
连续分级概率评分(Continuous Ranked Probability Score, CRPS)或“连续概率排位分数”是一个函数或统计量,可以将分布预测与真实值进行比较。
机器学习工作流程的一个重要部分是模型评估。这个过程本身可以被认为是常识:将数据分…
机器学习笔记之狄利克雷过程(六)预测任务求解
机器学习笔记之狄利克雷过程——预测任务求解引言回顾:基于狄利克雷过程的预测过程预测任务的求解过程引言
上一节引出了基于狄利克雷过程的预测任务,本节将对该预测任务进行求解。
回顾:基于狄利克雷过程的预测过程
在已知隐变量样本集合…
通过机器学习预测电网平均总负荷
文章目录0 概述1 研究动机2 相关工作3 统计学处理3.1 数据预处理3.2 季节性分析4 算法4.1 支持向量回归SVR4.2 聚类Clustering4.3 神经网络Neural Networks4.4 高斯过程回归 Gaussian Process Regression5 实施6 实验结果7 未来方向8 结论参考文献0 概述 该研究基于比利时Elia …
机器学习之模型评估与选择
一、模型评估与选择 分为五部分:1、经验误差及过拟合;2、评估方法‘;3、性能度量’;4、比较检验;5、偏差与方差。
1、经验误差与过拟合 错误率(error rate):分类错误的样本数占总样…
【计量经济学】虚拟变量
虚拟变量–潘登同学的计量经济学笔记 文章目录虚拟变量--潘登同学的计量经济学笔记对定性信息的描述只有一个虚拟变量的情形虚拟变量系数的解释虚拟变量的作用效果检验工资性别歧视因变量为对数形式的情况多个虚拟变量的情形虚拟变量系数的解释使用虚拟变量包含序数信息虚拟变量…
概率图模型--因子图
概率图模型–因子图 – 潘登同学的Machine Learning笔记 文章目录概率图模型--因子图 -- 潘登同学的Machine Learning笔记简单回顾概率图模型回顾贝叶斯网络简单回顾马尔可夫随机场(MRF)因子图将贝叶斯网络用因子图表示将马尔科夫随机场用因子图表示总结简单回顾概率图模型
概…
概率图模型--马尔可夫随机场
概率图模型–马尔可夫随机场 – 潘登同学的Machine Learning笔记 文章目录概率图模型--马尔可夫随机场 -- 潘登同学的Machine Learning笔记由贝叶斯网络过渡到马尔可夫链简单回顾贝叶斯网络由head-to-tail导出马尔可夫链马尔可夫随机场(MRF)马尔可夫随机场与马尔可夫链的关系马…
多分类任务ovo、ovr及softmax回归
多分类任务OVO、OVR及softmax回归 – 潘登同学的Machine Learning笔记 文章目录多分类任务OVO、OVR及softmax回归 -- 潘登同学的Machine Learning笔记简单回顾Logistic回归Logistic回归实现多分类问题One-vs-all(one-vs-rest)实战OVR对上次的鸢尾花数据进行多分类OVO(One vs On…
對隨機變數做線性變換後的期望值和協方差
對隨機變數做線性變換後的期望值和協方差假設X,b∈Rn,A∈Rmn\textbf{X},b \in \R^n, A \in R^{m \times n}X,b∈Rn,A∈Rmn,那麼使用A,bA,bA,b對X\textbf{X}X做線性變換後,其期望值如下: E[AX]AE[X]\operatorname{E}[A\textbf{X}] A \oper…
关于 CSP - J 和区间 dp 入门注意事项
1. 首先,复赛的时候
注意时间复杂度和空间大小 1.看题目时必须仔细,例如数组的大小在空间允许的情况下,多开10倍 2.如果采用暴力算法,记得剪枝或者记忆化 2.关于区间dp
常规模版:
for ...//枚举区间长度for ...//枚举左右两个端…
《推荐系统实践》 第三章 推荐系统冷启动问题 读书笔记
如何在没有大量用户数据的情况设计个性化推荐系统并且让用户对推荐结果满意从而愿意使用推荐系统,就是冷启动问题
冷启动问题简介
用户冷启动 用户冷启动主要解决如何给新用户做个性化推荐的问题。当新用户到来时,我们没有他的行为数据,所以也无法根据…
贝叶斯公式与全概率公式合并的理解
贝叶斯公式
贝叶斯的公式为: P(A∣B)P(AB)P(B)P(A | B) \frac{P(AB)}{P(B)} P(A∣B)P(B)P(AB) 若变为乘法那么就是 P(AB)P(B)∗P(A∣B)P(AB) P(B) * P(A | B) P(AB)P(B)∗P(A∣B) 也就是表示AB两件事情要一起发生的话,那么需要一件事(这…
R大数定律(Python切比雪夫不等式验证大数定律)模拟圆周率
大数定律
在概率论中,大数定律 (LLN) 是描述大量执行相同实验的结果的定理。 根据规律,大量试验所得结果的平均值应接近预期值,并随着试验次数的增加而趋于接近预期值。
LLN 很重要,因为它保证了一些随机事件的平均值的长期稳定…
数学杂谈:限制条件下的均匀分布考察
数学杂谈:限制条件下的均匀分布考察 1. 问题描述2. 问题解答 1. 答案2. 解析3. 蒙特卡洛模拟 3. 离散情况延拓 1. 正整数的情况2. 整数的情况3. N→∞N \to \inftyN→∞的情况 4. 误区分析 1. 问题描述
假设x1,...,xnx_1, ..., x_nx1,...,xn均为0∼10 \sim 10…
概率论与数理统计 Chapter4. 参数估计
概率论与数理统计 Chapter4. 参数估计 1. 基础概念 1. 总体2. 样品3. 统计量 1. 样本方差2. k阶原点矩3. k阶中心矩 2. 参数的点估计 1. 矩估计 1. 正态分布2. 指数分布3. 均匀分布4. 二项分布5. 泊松分布 2. 极大似然估计 1. 正态分布2. 指数分布3. 二项分布4. 均匀分布5. 泊…
为什么十赌九输?赌博中怎么才能使获胜概率最大?
1685年,伯努利也是以研究赌博术为目的开始写作一部真正奠定“概率论”基础的历史性巨著《猜度术》,在这本著作当中,他创立了概率论中的第一极限定理:“伯努利大数定律”。“大数定理“与“中心极限定理”一起,成为了现…
CF1781F Bracket Insertion(2700*) 题解(括号匹配DP)
题目
题面 简要题意: 你需要执行一下步骤 n n n 次来构建括号序列: ⋅ \cdot ⋅ 等概率选择一个空位(若当前有 k k k 个字符,则有 k 1 k 1 k1 个空位)。 ⋅ \cdot ⋅ 以 p p p 的概率插入字符…
Jellyfish and EVA
这道题目实在没有什么好的办法去描述状态空间,只能感性理解一下,等对概率的理解更深了再来吧。。。 发现这是一道概率DP,而且满足拓扑序,我们直接倒序转移就好了 设\(f_i\)表示从第\(i\)个点到第\(n\)个点的概率,我们发…
完全平方数(蓝桥杯,acwing,数论)
题目描述:
一个整数 a 是一个完全平方数,是指它是某一个整数的平方,即存在一个整数 b,使得 ab^2。
给定一个正整数 n,请找到最小的正整数 x,使得它们的乘积是一个完全平方数。
输入格式:
输…
聚类算法的先验基础知识
聚类算法的先验基础知识 1. 瑞利商2. 谱定理3. 联合概率4. 条件概率分布5. 边缘分布6. 贝叶斯定理7. 有向图8. 拉格朗日乘子定理 下一篇将介绍整理各种聚类算法,包括k-means,GMM(Guassian Mixture Models, 高斯混合),EM(Expectation Maximiza…
概率论和数理统计(二) 数字特征与大数定律
前言
有了“概率”数据,怎么反应情况.数学期望与方差,大数,极限
数学期望
期望是数字特征之一,其描述的是随机试验在同样的机会下重复多次,所有那些可能状态的平均结果.
平均数和加权平均数 离散型随机变量期望 连续型随机变量期望 随机变量函数的期望 g ( x , …
两个状态的马尔可夫链
手动推导如下公式。
证明:
首先将如下矩阵对角化: { 1 − a a b 1 − b } \begin {Bmatrix} 1-a & a \\ b & 1-b \end {Bmatrix} {1−aba1−b}
(1)求如下矩阵的特征值: { 1 − a a b 1 − b } { x 1 x 2 } λ { x 1 x 2 }…
机器学习:隐马尔可夫模型(HMM)
后续会回来补充代码 1 隐马尔可夫模型 隐马尔可夫模型(Hidden Markov Model,HMM)是可用于标注问题的统计学模型,描述由隐藏的马尔可夫链随机生成观测序列的过程。
1.1 数学定义 隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成…
【TODO】米哈游20230813笔试第三题
是计算抽中什么当期五星的期望。 现在的程序结果是99.6087。结果不对,有时间再调。 #include <iostream>
#include <bits/stdc.h>
typedef long long LL;
using namespace std;int n 90;
double p;
// double min_p 1e-7;
double min_p 0.0000000000…
【考研数学】概率论与数理统计 —— 第二章 | 一维随机变量及其分布(1,基本概念与随机变量常见类型)
文章目录 引言一、一维随机变量及其分布1.1 随机变量1.2 分布函数 二、随机变量常见类型及分布2.1 离散型随机变量2.2 连续型随机变量及概率密度函数 写在最后 引言
暑假接近尾声了,争取赶一点概率论部分的进度。 一、一维随机变量及其分布
1.1 随机变量
设随机试…
【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布(1,二维连续型和离散型随机变量基本概念与性质)
文章目录 引言一、二维随机变量及分布1.1 基本概念1.2 联合分布函数的性质 二、二维离散型随机变量及分布三、多维连续型随机变量及分布3.1 基本概念3.2 二维连续型随机变量的性质 写在最后 引言
隔了好长时间没看概率论了,上一篇文章还是 8.29 ,快一个…
利用百分位点函数ppf计算置信区间上下限
百分位点函数(Percent Point Function,PPF),也称为逆分布函数或分位数函数,是概率分布函数的逆运算。它的作用是根据给定的累积概率值,计算随机变量的值,使得该值以下的累积概率等于给定的概率。…
概率论--随机事件与概率--贝叶斯公式--随机变量
目录
随机事件与概率
概念
为什么要学习概率论
随机事件与随机事件概率
随机事件
随机事件概率
贝叶斯公式
概念
条件概率
概率乘法公式
贝叶斯公式
举个栗子
随机变量 随机变量的定义
随机变量的分类
离散型随机变量
连续型随机变量 随机事件与概率
概念 …
强化学习之Makov决策
离散时间Makov决策过程
离散时间的Markov决策过程模型可以在离散时间的智能体/环境接口的基础上进一步引入具有Markov性的概率模型得到。
奖励,汇报和价值函数
对于回合制任务,驾驶某一回合在第t步达到终止状态,则从步骤t(t<T)以后的回报ÿ…
利用norm.ppfnorm.interval分别计算正态置信区间[实例]
scipy.stats.norm.ppf用于计算正态分布的累积分布函数CDF的逆函数,也称为百分位点函数。它的作用是根据给定的概率值,计算对应的随机变量值。scipy.stats.norm.interval:用于计算正态分布的置信区间,可指定均值和标准差。scipy.st…
利用t.ppft.interval分别计算T分布置信区间[实例]
scipy.stats.t.interval用于计算t分布的置信区间,即给定置信水平时,计算对应的置信区间的下限和上限。
scipy.stats.t.ppf用于计算t分布的百分位点,即给定百分位数(概率)时,该函数返回给定百分位数对应的t…
极大似然估计概念的理解——统计学习方法
目录 1.最大似然估计的概念的理解1
2.最大似然估计的概念的理解2
3.最大似然估计的概念的理解3
4.例子 1.最大似然估计的概念的理解1 最大似然估计是一种概率论在统计学上的概念,是参数估计的一种方法。给定观测数据来评估模型参数。也就是模型已知,参…
第2章 随机变量及概率分布
# 第2章 随机变量及概率分布 [TOC]
2.1 一维随机变量
2.1.1 随机变量的概念
随机变量就是“其值随机会而定”的变量。 用随机变量加限制的方法,可以表示一个事件。 按取值全体的性质,随机变量分为两大类: - 离散型随机变量 - 连续型随…
【力扣面试】面试题 05.08. 绘制直线(描述恶心人)
【力扣面试】面试题 05.08. 绘制直线 文章目录题目解题思路代码题目 绘制直线。有个单色屏幕存储在一个一维数组中,使得32个连续像素可以存放在一个 int 里。屏幕宽度为w,且w可被32整除(即一个 int 不会分布在两行上),…
马尔科夫型决策以及使用python计算方法
一、马尔可夫性
考察某工厂一台自动加工机的工作状态。该机器有两种工作状态:正常状态和故障状态。在每个整数钟点的起始时刻检查机器的工作情况,若机器处于正常状态,则让它继续工作;若机器处于故障状态,则对他进行检…
数论——欧拉函数及欧拉打表
欧拉函数的功能:用于求小于n的与n互质数的个数 欧拉函数的作用:用于求小于n的与n互质数的个数
欧拉函数的公式: φ(n)n*(1-1/p1)(1-1/p2)(1-1/p3)*(1-1/p4)……(1-1/pn), 其中p1, p2……pn为n的所有质因数,n是不为0的整数。φ(1)…
概率公式中的分号、逗号、竖线
【2021-07-02更新】补充一个例子:GDAS中有这样一个公式: minαE(x′,y′)∼DV−logPr(y′∣x′;α,ωα∗)s.t. ωα∗argminωE(x,y)∼DT−logPr(y∣x;α,ωα)\begin{array}{r} \min _{\alpha} \mathbb{E}_{\left(x^{\prime}, y^{\prime…
机器学习算法基础:硬核高斯分布
提前放狠话:看不懂打si我吧,真的很细节了。 提前了解: 1、极大似然估计(MLE)、最大后验概率估计(MAP)、贝叶斯估计区别 2、正定矩阵与半正定矩阵定义性质与理解 3、马氏距离和欧式距离详解 4、参…
概率统计Python计算:样本数据直方图绘制
对总体XXX的一次具体抽样,得到一个容量为nnn的样本观测值(x1,x2,⋯,xn)(x_1,x_2,\cdots,x_n)(x1,x2,⋯,xn)。记amin{x1,x2,⋯,xn}amin\{x_1,x_2,\cdots,x_n\}amin{x1,x2,⋯,xn},bmax{x1,x2,⋯,xn}bmax\{x_1,x_2,\cdots,x_n\}bmax{x1,x2,…
【考研数学】概率论与数理统计 | 第一章——随机事件与概率(2,概率基本公式与事件独立)
文章目录 引言四、概率基本公式4.1 减法公式4.2 加法公式4.3 条件概率公式4.4 乘法公式 五、事件的独立性5.1 事件独立的定义5.1.1 两个事件的独立5.1.2 三个事件的独立 5.2 事件独立的性质 写在最后 引言
承接上文,继续介绍概率论与数理统计第一章的内容。 四、概…
概率密度函数 累积分布函数
概率密度函数:是指想要求得面积的图形表达式,注意只是表达式,要乘上区间才是概率,所以概率密度并不是概率,而是概率的分布程度。
为什么要引入概率密度,可能是因为连续变量,无法求出某个变量的…
【数学】【书籍阅读笔记】【概率论】应用随机过程概率论模型导论 by Sheldon M.Ross 第一章 概率论引总结与习题题解 【更新中】
文章目录 前言1 第一章 概率论引论 总结1.1 样本空间与事件1.2 定义在事件上的概率1.3 条件概率1.4 独立事件 2 一些有用的重要结论/公式/例题3 重要例题例 1.11 3 习题题解题1题2 4 习题总结 前言
1 第一章 概率论引论 总结 第一章从事件的角度引出样本空间、事件、概率的基本…
LabVIEW计算测量路径输出端随机变量的概率分布密度
LabVIEW计算测量路径输出端随机变量的概率分布密度
今天,开发算法和软件来解决计量综合的问题,即为特定问题寻找最佳测量算法。提出了算法支持,以便从计量上综合测量路径并确定所开发测量仪器的测量误差。测量路径由串联的几个块组成&#x…
概率论与数理统计学习笔记(7)——全概率公式与贝叶斯公式
目录 1. 背景2. 全概率公式3. 贝叶斯公式 1. 背景
下图是本文的背景内容,小B休闲时间有80%的概率玩手机游戏,有20%的概率玩电脑游戏。这两个游戏都有抽卡环节,其中手游抽到金卡的概率为5%,端游抽到金卡的概率为15%。已知小B这天抽…
Z检验|T检验|样本标准差S代替总体标准差 σ
Z检验也叫做正态分布的标准正态分布变量检验。它通常用于大样本(样本容量大于30)且总体标准差已知的情况下,用于比较样本均值与总体均值之间的差异是否显著。
Z检验的基本思想都是计算样本均值与参考值或另一个样本均值之间的差异࿰…
极限中的无穷小量和无穷大量
目录
极限中的无穷小量
无穷小量的比较
无穷小量的性质
无穷大量和无穷小量的关系 极限中的无穷小量 在高等数学数学分析中,无穷小量是一个以数0为极限的变量,即当自变量x无限接近于某个点(或绝对值无限增大)时,函…
【概率论】常用的离散分布
文章目录 选择题 选择题 设随机变量 X ∼ B ( 2 , p ) , Y ∼ B ( 3 , p ) X \sim B(2,p),Y\sim B(3, p) X∼B(2,p),Y∼B(3,p),且 P { X ≥ 1 } 5 9 P \{ X \ge 1 \} \frac {5}{9} P{X≥1}95,则P{Y≥1}()。 A. 8 27 \frac {8}{27} 278…
宋浩概率论笔记(六)样本与统计量
参数估计的入门章节,为后面的参数估计与假设检验铺垫基础,难点在于背诵公式,此外对于统计量的理解一定要清晰——本质是多个随机变量复合而成的函数~
PT@事件间的运算规律
文章目录 abstract事件间的运算规律👺基本事实全集(必然事件)&空集(不可能事件)相关运算🎭前提和相应真命题👺恒等式 自反律交换律结合律分配律👺对偶律(德摩根律)附加定理👺消去律不成立👺判定事件为空…
(二)随机变量的数字特征:探索概率分布的关键指标
文章目录 🍋1. 随机变量的数学期望🍋1.1 离散型随机变量的数学期望🍋1.2 连续型随机变量的数学期望 🍋2. 随机变量函数的数学期望🍋2.1 一维随机变量函数的数学期望🍋2.2 二维随机变量函数的数学期望 &…
Hoeffing不等式
在李航老师的统计学习方法(第一版中) H o e f f i n g 不等式 Hoeffing不等式 Hoeffing不等式是这样子给出的
设 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN是独立随机变量,且 X i ∈ [ a i , b i ] , i 1 , 2 , . . . ,…
马尔可夫链预测举例——钢琴销售的存贮策略
问题概述 一家钢琴专卖店,根据以往的销售经验,平均每周只能售出一架钢琴,现在经理指定的存贮策略是,每周末检查库存存量,仅当库存量为零时,才订购3架供下周销售;否则就不订购。试估计这种策略下…
概率论几种易混淆的形式
正态分布标准型 x − μ σ \frac{x - \mu}{\sigma} σx−μ
大数定律形式 P { X ≤ ∑ i 1 n x i − n μ n σ 2 } ∫ − ∞ X 1 2 π e − x 2 2 d x P\{X \le \frac{\sum_{i 1}^{n}x_i -n\mu}{\sqrt{n\sigma^2}} \} \int _{-\infty}^{X}\frac{1}{\sqrt{2\pi}}e^{-\fr…
统计的基本概念及抽样分布
文章目录 🍋引言🍋总体(Population)🍋总体参数 🍋样本(Sample)🍋随机样本🍋样本统计量 🍋统计量(Statistic)🍋…
【考研数学】概率论与数理统计 —— 第四章 | 随机变量的数字特征
文章目录 一、随机变量的数学期望1.1 概念1. 一维离散型随机变量的数学期望2. 一维连续型随机变量的数学期望3. 二维离散型随机变量的数学期望4. 二维连续型随机变量的数学期望 1.2 数学期望的性质 二、随机变量的方差2.1 概念2.2 计算公式2.3 方差的性质2.4 常见随机变量的数学…
估算总体标准差的极差均值估计法sigma = R/d2
总体标准差的估算值可以通过将平均极差除以合适的常数因子d2来计算。这个估算方法是用于估算总体标准差的一种常见方法,尤其在质量控制和过程监控中经常使用。
总体标准差的估算值 (平均极差) / d2
其中:
"总体标准差的估算值" 表示用极差…
Python+Gurobi求解SWTA问题
前言
静态武器目标分配(static weapon-target assignment,WTA)问题是军事领域的著名问题,也是分配问题中的研究热点之一。SWTA问题易于描述但是难以求解,自1958年提出以来,大量学者对其进行了研究…
概率论和数理统计(一)基本概念
前言
生活中对于事件的发生,可以概括为
确定现象:在一定条件下必然发生,如日出随机现象:在个别试验中其结果呈现出不确定性,在大量重复试验中其结果又具有统计规律的现象,称之为随机现象。
随机现象的特点ÿ…
深度学习——(生成模型)DDPM
前置数学知识
1、先验概率和后验概率
先验概率:根据以往经验和分析得到的概率,它往往作为“由因求果”问题中的“因”出现,如 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1)
后验概率:指在得到“结果”的信息后重新修正的概率,是…
优思学院|精益与六西格玛双剑合璧达至降本增效
降本增效是指企业通过降低成本,提高生产效率和经营效益的管理策略。具体来说,企业可以通过优化生产技术和方法、改善管理流程、提高员工效能等方式实现降本增效。
提到降本增效或提升生产效率,第一个被提出来检讨的一定是直接部门。但是如果…
Logistics 逻辑回归概念
1. sigmoid函数
逻辑回归算法的拟合函数,叫做sigmoid函数:
函数图像如下(百度图片搜到的图): sigmoid函数是一个s形曲线,就像是阶跃函数的温和版,阶跃函数在0和1之间是突然的起跳,…
累计概率分布、概率分布函数(概率质量函数、概率密度函数)、度量空间、负采样(Negative Sampling)
这里写自定义目录标题 机器学习的基础知识累计概率分布概率分布函数度量空间负采样(Negative Sampling)基于分布的负采样(Distribution-based Negative Sampling):基于近邻的负采样(Neighbor-based Negativ…
20240323-1-条件随机场面试题CRF
条件随机场面试题
1. 简单介绍条件随机场 条件随机场(conditional random field,简称 CRF)是给定一组输入随机变量条 件下另一组输出随机变量的条件概率分布模型,其特点是假设输出随机变量构成马尔可夫随机场,是一种鉴…
一个概率论例题引发的思考
浙江大学版《概率论与梳理统计》一书中的,第13章第1节例2如下:
这个解释和模型比较简单易懂。接下来,第2节的例2是一个关于此模型的题目: 在我自己的理解中,此题的解法跟上一个题目一样,第二级传输后&…
链式法则:概率论描述语言模型
目录 1.事件相互独立
2.链式法则
3.示例
4.语言模型中的链式法则 1.事件相互独立
事件相互独立就是:一个事件的发生与否,不会影响另外一个事件的发生。
当a和b两个事件互相独立时,有: P(a | b) P(a) 推广到3个事件就有下面…
Lilliefors正态性检验(一种非参数统计方法)
Lilliefors检验(也称为Kolmogorov-Smirnov-Lilliefors检验)是一种用于检验数据是否符合正态分布的统计检验方法,它是Kolmogorov-Smirnov检验的一种变体,专门用于小样本情况。与K-S检验不同,Lilliefors检验不需要假定数…
Kolmogorov-Smirnov正态性检验
Kolmogorov-Smirnov正态性检验是一种统计方法,用于检验数据集是否服从正态分布。其基本原理和用途如下:
基本原理:
假设检验:Kolmogorov-Smirnov检验基于一个假设,即待检验的数据集服从特定的理论正态分布。计算累积…
参数估计(一)(点估计)
文章目录 点估计和估计量的求法点估计概念矩估计法极大似然估计法 参考文献 参数估计是数理统计中重要的基本问题之一。通常,称参数的可容许值的全体为参数空间,并记为 Θ \Theta Θ。所谓参数估计就是由样本对总体分布所含的未知参数做出估计。另外&am…
机器学习技术栈—— 概率学基础
机器学习技术栈—— 概率学基础 先验概率、后验概率、似然概率总体标准差和样本标准差 先验概率、后验概率、似然概率
首先 p ( w ∣ X ) p ( X ∣ w ) ∗ p ( w ) p ( X ) p(w|X) \frac{ p(X|w)*p(w)}{p(X)} p(w∣X)p(X)p(X∣w)∗p(w) 也就有 p ( w ∣ X ) ∝ p ( X ∣ …
11.16~11.19绘制图表,导入EXCEL中数据,进行拟合
这个错误通常是由于传递给curve_fit函数的数据类型不正确引起的。根据你提供的代码和错误信息,有几个可能的原因: 数据类型错误:请确保ce_data、lg_data和product_data是NumPy数组或类似的可迭代对象,且其元素的数据类型为浮点数。…
SPSS多维尺度分析
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件请点击此链接下…
【数学建模】《实战数学建模:例题与讲解》第六讲-假设检验(含Matlab代码)
【数学建模】《实战数学建模:例题与讲解》第六讲-假设检验(含Matlab代码) 基本概念假设检验的步骤错误类型在数学建模中的应用三种常用的统计检验方法t检验(t-Test)方差分析(ANOVA)Kolmogorov-S…
信息检索与数据挖掘 | (七)概率检索模型
文章目录 📚基本概率论知识📚概率排序原理PRP-probability ranking principle📚二值独立模型BIM-Binary Independence Model📚Okapi BM25模型 出于一些追求完整性的强迫症,开始做考完试了梳理知识点博客的离谱行为&…
【深度学习】S2 数学基础 P6 概率论
目录 基本概率论概率论公理随机变量 多个随机变量联合概率条件概率贝叶斯定理求和法则独立性 期望与方差小结 基本概率论
机器学习本质上,就是做出预测。而概率论提供了一种量化和表达不确定性水平的方法,可以帮助我们量化对某个结果的确定性程度。
在…
趣学贝叶斯定理:贝叶斯定理的先验概率、似然和后验概率(2)
4. 比较非归一化的后验概率
首先,我们需要求出两个后验概率的比值 P ( D ∣ H 1 ) P ( D ∣ H 2 ) \frac{P(D|H1)}{P(D|H2)} P(D∣H2)P(D∣H1)
接下来,用贝叶斯定理将其中的每一项都展开。 所以这个后验概率比值告诉我们,在不知道P(D)的…
【考研数学】概率论与数理统计 | 第一章——随机事件与概率(1)
文章目录 一、随机试验与随机事件1.1 随机试验1.2 样本空间1.3 随机事件 二、事件的运算与关系2.1 事件的运算2.2 事件的关系2.3 事件运算的性质 三、概率的公理化定义与概率的基本性质3.1 概率的公理化定义3.2 概率的基本性质 写在最后 一、随机试验与随机事件
1.1 随机试验 …
【量化课程】02_4.数理统计的基本概念
2.4_数理统计的基本概念
数理统计思维导图 更多详细内容见notebook
1.基本概念
总体:研究对象的全体,它是一个随机变量,用 X X X表示。
个体:组成总体的每个基本元素。
简单随机样本:来自总体 X X X的 n n n个相互…
20231018 自然常数的存在性
1
除了使用魏尔斯特拉斯定理,还可以使用不定式的洛必达法则来证明这一极限。首先,将 lim x → ∞ ( 1 1 x ) x \lim _{x \rightarrow \infty}\left(1\frac{1}{x}\right)^x x→∞lim(1x1)x 写成以下形式: lim x → ∞ ( 1 1 x ) …
PKU 概率论+数理统计 期中考复习总结
这里写目录标题 计算条件概率计算概率(放回与不放回)生成随机数算法Uniformity (test of frequency)1.Chi-Square test2.Kolmogorov-Sminov test Independence (test of autocorrelation)Runs test Acceptance-rejection methodmethod方法1:建…
PKU 概率论+数理统计+建模 期中考复习总结
目录 计算条件概率计算概率(放回与不放回)生成随机数算法Linear Congruential Method判断是否是full period Uniformity (test of frequency)1.Chi-Square testmethodreminderexample 2.Kolmogorov-Sminov testmethodexample Independence (test of auto…
模式识别——高斯分类器
模式识别——高斯分类器 需知定义特殊情况(方差一致)Sigmoid 需知
所有问题定义在分类问题下,基于贝叶斯决策
定义
条件概率为多元高斯分布,此时观测为向量 X X 1 , X 2 , . . . , X n X{X_1,X_2,...,X_n} XX1,X2,...,Xn…
【知识串联】概率论中的值和量(随机变量/数字特征/参数估计)【考研向】【按概率论学习章节总结】(最大似然估计量和最大似然估计值的区别)
就我的概率论学习经验来看,这两个概念极易混淆,并且极为重点,然而,在概率论的前几章学习中,如果只是计算,对这方面的辨析不清并没有问题。然而,到了后面的参数估计部分,却可能出现问…
检验数据是否符合正态分布的统计方法
Shapiro-Wilk检验、Kolmogorov-Smirnov检验和Anderson-Darling检验都是常见用于检验数据是否符合正态分布的统计方法。以下是它们的简要介绍: Shapiro-Wilk检验: Shapiro-Wilk检验是一种用于小到中等样本量的检验方法。它的原假设是数据来自正态分布。如…
方差分析的核心概念“方差分解“
方差是统计学中用来衡量数据集合中数值分散或离散程度的一种统计量。它表示了数据点与数据集合均值之间的差异程度,即数据的分散程度。方差越大,表示数据点更分散,而方差越小,表示数据点更集中。
方差的计算公式如下:…
【矩阵分解】PCA - 主成分分析中的数学原理
前言
本文主要对PCA主成分分析中的数学原理进行介绍,将不涉及或很少涉及代码实现或应用,阅读前请确保已了解基本的机器学习相关知识。
文章概述
PCA主成分分析属于矩阵分解算法中的入门算法,通过分解特征矩阵来实现降维。
本文主要内容&a…
SPSS多因素方差分析
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件请点击此链接下…
【统计学】独立同分布
1. 概念
独立同分布是统计学中的一个重要概念,指的是在概率论和统计学中常见的一种假设,即一组随机变量之间相互独立,并且具有相同的概率分布。
具体来说,如果一组随机变量 {X₁, X₂, …, Xₙ} 是相互独立的,意味着…
大白话扩散模型(无公式版)
背景
传统的图像生成模型有GAN,VAE等,但是存在模式坍缩,即生成图片缺乏多样性,这是因为模型本身结构导致的。而扩散模型拥有训练稳定,保持图像多样性等特点,逐渐成为现在AIGC领域的主流。
扩散模型
正如…
概率论和数理统计(一)概率的基本概念
前言
生活中对于事件的发生,可以概括为
确定现象:在一定条件下必然发生,如日出随机现象:在个别试验中其结果呈现出不确定性,在大量重复试验中其结果又具有统计规律的现象,称之为随机现象。
随机现象的特点ÿ…
SLAM 14 notes
4.23 推导 f ( x ) f(x) f(x)在点a处的泰勒展开 f ( x ) ∑ n 0 ∞ f ( n ) a n ! ( x − a ) n f(x) \sum_{n0}^\infty \frac{f^{(n)}a}{n!}(x-a)^n f(x)∑n0∞n!f(n)a(x−a)n l n x lnx lnx的n阶导数 l n ( n ) x ( − 1 ) n − 1 ( n − 1 ) ! x n ln^{(n)}x \fr…
关于利用talib.macd函数计算macd指标与同花顺不一致的问题
首先我们来看下Macd指标计算方法:
12日EMA的计算:EMA12 前一日EMA12 * 11/13 今日收盘 * 2/13
26日EMA的计算:EMA26 前一日EMA26 * 25/27 今日收盘 * 2/27
差离值(DIF)的计算: DIF EMA12 - EMA26
…
【MATLAB】全网唯一的11种信号分解+模糊熵(近似熵)联合算法全家桶
有意向获取代码,请转文末观看代码获取方式~
大家吃一顿火锅的价格便可以拥有18种信号分解算法,绝对不亏,知识付费是现今时代的趋势,而且都是我精心制作的教程,有问题可随时反馈~也可单独获取某一算法的代码࿰…
经管博士科研基础【25】概率论中的相关基础概念
1. Support
在概率论中,"support"(支撑集)是指随机变量可能取值的集合。对于离散型随机变量,支撑集包含了所有可能的取值;而对于连续型随机变量,支撑集是指其密度函数或概率质量函数非零的区域。…
对全概率公式、贝叶斯公式的理解
目录
一、全概率公式
二、贝叶斯公式
三、综合题目 一、全概率公式 定义: 在事件A发生的前提下,事件A又作为事件B发生的条件,这样两两一组的概率总和,就为概率论公式。题目通常问的是一整个事件的概率。别急,请看例题。 1.18 …
AMP State Evolution的计算:以伯努利高斯先验为例
AMP State Evolution (SE)的计算 t 1 t1 t1时, E ( t ) E [ X 2 ] \mathcal E^{(t)} \mathbb E [X^2] E(t)E[X2],SE的迭代式为 τ r ( t ) σ 2 1 δ E ( t ) E ( t 1 ) E ∣ η ( t ) ( X Z ) − X ∣ 2 , Z ∼ N ( 0 , τ r ( t ) ) \begin{a…
概率论与数理统计-第4章 随机变量的数字特征
第4章 随机变量的数字特征
4.1数学期望
一、离散型随机变量的数学期望
定义1设离散型随机变量X的概率分布为 P{Xxi}pi,i1,2,…,如果级数绝对收敛,则定义X的数学期望(又称均值)为
二、连续型随机变量的数学期望
定义2设X是连续型随机变量…
假设检验(一)假设检验的基本概念
文章目录 假设与检验规则两类错误假设检验的一般步骤参考文献 假设检验(Test of Hypothesis)是指,先对总体或总体的性质提出某项假设,再利用样本所提供的信息对提出的假设进行检验,以判断该假设是否成立。假设检验可分…
【考研数学】概率论与梳理统计 —— 第三章 | 二维随机变量及其分布(1,二维连续型和离散型随机变量基本概念与性质)
文章目录 引言一、二维随机变量及分布1.1 基本概念1.2 联合分布函数的性质 二、二维离散型随机变量及分布三、多维连续型随机变量及分布3.1 基本概念3.2 二维连续型随机变量的性质 写在最后 引言
隔了好长时间没看概率论了,上一篇文章还是 8.29 ,快一个…
概率论与数理统计-第五章 数理统计的基础知识
第五章 数理统计的基础知识
由于大量随机现象必然呈现出它的规律性,故理论上只要对随机现象进行足够多次的观察,研究对象的规律性就一定能清楚地呈现出来,但实际上人们常常无法对所研究的对象的全体(或总体)进行观察&…
Matlab随机数的产生
1、常见分布随机数的产生
1.1 二项分布
在贝努力试验中,某事件A发生的概率为p,重复该实验n次,X表示这n次实验中A发生的次数,则随机变量X服从的概率分布律(概率密度)为
记为 binopdf(x,n,p) p…
单样本T检验|独立样本T检验|配对样本T检验(绘图)
学生 t 检验的基本思想是通过比较两组数据的均值以及它们的方差来判断是否存在显著差异。下面更详细地解释了学生 t 检验的基本思想: 均值比较:学生 t 检验的首要目标是比较两组数据的均值。我们通常有一个零假设(null hypothesis)…
假设检验(二)(正态总体参数的假设检验)
文章目录 一个正态总体的情形总体均值 μ \mu μ 的检验总体方差 σ 2 \sigma^2 σ2 的检验—— χ 2 \chi^2 χ2 检验 两个正态总体的情形两总体均值差的检验—— t t t 检验两总体方差比的检验—— F F F 检验 参考文献 在作假设检验时,若检验统计量服从正态分布…
用分布函数定义的随机变量的独立性的合理性
随机变量的独立性是这样定义的:
如果对任意 x , y x, y x,y 都有 P { X ≤ x , Y ≤ y } P { X ≤ x } P { Y ≤ y } P\{X\leq x,Y\leq y\} P\{X\leq x \}P\{Y\leq y\} P{X≤x,Y≤y}P{X≤x}P{Y≤y} 即 F ( x , y ) F X ( x ) F Y ( y ) F(x,y)F_X(x)F_Y(y) F…
【概率统计】如何理解概率密度函数及核密度估计
文章目录 概念回顾浅析概率密度函数概率值为0?PDF值大于1?一个栗子 核密度估计如何理解核密度估计核密度估计的应用 总结 概念回顾 直方图(Histogram):直方图是最直观的一种方法,它通过把数据划分为若干个区…
【论文阅读】Bayes’ Rays:神经辐射场的不确定性量化
【论文阅读】Bayes’ Rays:神经辐射场的不确定性量化 1. Introduction2. Related work3. Background3.2. Neural Laplace Approximations 4. Method4.1. Intuition4.2. Modeling perturbations4.3. Approximating H4.4. Spatial uncertainty 5. Experiments & A…
在AWS Lambda中使用FFmpeg处理m3u8视频流
大纲 1 部署有FFmpeg功能的Lambda环境1.1 部署层1.2 部署代码1.2.1 FFmpeg指令1.2.2 代码 2 配置Lambda角色权限2.1 选择角色类型2.2 设置权限2.3 保存角色2.4 绑定角色 参考文献 在直播里领域,我们经常需要对视频流进行处理。FFmpeg则是该领域中处理的利器。这篇文…
【考研数学】概率论与数理统计 —— 第五章 | 大数定律与中心极限定理
文章目录 一、切比雪夫不等式二、大数定律2.1 依概率收敛的定义2.2 常见的大数定律 三、中心极限定理写在最后 一、切比雪夫不等式
定理 1 —— (切比雪夫不等式)设随机变量 X X X 的方差存在,则对任意的 ε > 0 \varepsilon>0 ε&g…
【贝叶斯分析】计算机科学专业博士作业一
1、 1964 年,一对跨种族夫妇在洛杉矶被判抢劫罪,主要是因为他们的个人资料符合极不可能的情况,而这一资料与目击者的报告相符。据目击者所述,这两名劫匪是: 男人留着小胡子 、男人是黑人 、女人绑着马尾 、女人是金发 …
概率论之 证明 正态分布的上a 分位点的对称的性质
公式(Z(a) -Z(1-a)) 表示正态分布的上(a)分位点与下(1-a)分位点在分布曲线上关于均值的对称性。 左侧 (Z(a)): 这是分布曲线上累积概率为(a)的那个点。也就是说,这是一个使得这个点及其左侧的面积占据整个曲线下方(a)的位置。 右侧 (Z(1-a))࿱…
朴素贝叶斯(基于概率论)
释义
贝叶斯定理是“由果溯因”的推断,所以计算的是"后验概率" 其中: P(A|B) 表示在事件 B 已经发生的条件下,事件 A 发生的概率。 P(B|A) 表示在事件 A 已经发生的条件下,事件 B 发生的概率。 P(A) 和 P(B) 分别表示事…
Scott-Knott ESD test
1.官方介绍
原英文链接:https://cran.r-project.org/web/packages/ScottKnottESD/ScottKnottESD.pdf 斯科特-克诺特效应大小差异(Scott-Knott Effect Size Difference , ESD)检验是一种均值比较方法,它利用分层聚类将一组处理均值…
【自用重要】概率论中θ和θ尖的区别【计算时的一般方法】
θ就相当于x,是一个值。 θ尖就相当于X,是一个量。
在做分布函数的时候,最好把θ尖换成Z的形式,因为他们都是量,这样比较好看。 在做不等式的时候,一般把量放在中间进行计算,因为随机变量有分…
大数据机器学习 - 似然函数:概念、应用与代码实例
文章目录 大数据机器学习 - 似然函数:概念、应用与代码实例一、概要二、什么是似然函数数学定义似然与概率的区别重要性举例 三、似然函数与概率密度函数似然函数(Likelihood Function)定义例子 概率密度函数(Probability Density…
50 个具有挑战性的概率问题 [第 5 部分]:方形硬币
一、说明 你好,我最近对与概率相关的问题产生了兴趣。我偶然发现了 Frederick Mosteller 所著的《五十个具有挑战性的概率问题及其解决方案》这本书。我认为创建一个系列来讨论这些可能作为面试问题出现的迷人问题会很有趣。每篇文章仅包含 1 个问题,使其…
【概率论教程01】对贝叶斯定理的追忆
一、说明 贝叶斯定理,是一个需要反复体悟的道理,不是说公式解释清除就算Grasp,而是需要反复在实际项目中发挥,才能算掌握了。而实际应用中,并不是简单给出条件就可以套用,而是隐藏在迷雾一样的事实中&#…
一个特殊级数的敛散性判断
海涅定理
若函数 f ( x ) f(x) f(x)在 x 0 x_0 x0的去心领域 U ( x 0 , δ ) U(x_0,\delta) U(x0,δ)内有定义,则 lim x → x 0 f ( x ) A \lim_{x\rightarrow x_0}f(x)A limx→x0f(x)A的充要条件是:对任意以 x 0 x_0 x0为极限且包含于 U…
SPSS单样本K-S检验
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件请点击此链接下…
优思学院|质量工程师在汽车行业待遇好吗?
优思学院认为质量工程师在汽车行业的待遇有可能相对较好的。随着中国汽车品牌在国内市场的崛起,特别是在电动汽车领域的增长,质量工程师在保障产品质量和安全性方面变得非常重要。由于中国汽车制造商对产品质量的高度重视,质量工程师在制定和…
【概率方法】重要性采样
从一个极简分布出发
假设我们有一个关于随机变量 X X X 的函数 f ( X ) f(X) f(X),满足如下分布 p ( X ) p(X) p(X)0.90.1 f ( X ) f(X) f(X)0.10.9
如果我们要对 f ( X ) f(X) f(X) 的期望 E p [ f ( X ) ] \mathbb{E}_p[f(X)] Ep[f(X)] 进行估计࿰…
概率论和数理统计(三)数理统计基本概念
前言
“概率论”是给定一个随机变量X的分布F(x),然后求某事件A概率 P ( x ∈ A ) P(x \in A) P(x∈A)或者随机变量X的数字特征.“统计”是已知一组样本数据 { x 1 , x 2 , . . . x n } \{x_1,x_2,...x_n\} {x1,x2,...xn},去求分布F(x)
统计的基本概念
在统计中&#x…
【模糊综合评价方法】
文章目录 1. 引言简介模糊综合评价法的背景与发展模糊综合评价法的重要性与应用领域 2. 模糊综合评价法的基本原理模糊集合与模糊关系的概念模糊综合评价的基本步骤 3. 模糊综合评价法的关键技术模糊关系矩阵的构造方法权重的确定方法模糊合成的方法 4. 模糊综合评价法在电子商…
@分布之间的关系 --------从分布之间的关系来理解随机现象、进而理解概率论
分布之间的关系 --------从分布之间的关系来理解随机现象、进而理解概率论 文章目录 关系分类 关系分类
概率分布之间的关系分两类:
变换、变形 作用于随机变量、概率分布,产生新分布 例如 随机变量的和、随机变量的乘积、随机变量的函数极限分布 当某些参数取极…
考研数学一——概率论真题——自我总结题型整理(总分393)
系列文章目录
终于考完研了,本人考的是南京航空航天大学的仪器科学与技术,英一数一电路,以下是成绩单:
平时习惯整理自己的学习体系,以下是一个记录。 其实,每个人都应该训练,看到某一类题目…
参数估计(三)区间估计
文章目录 区间估计的概念一个正态总体的情形 μ \mu μ 的区间估计 σ 2 \sigma^2 σ2 的区间估计 两个正态总体的情形 μ 1 − μ 2 \mu_1-\mu_2 μ1−μ2 的区间估计 参考文献 区间估计的概念
对未知参数来说,我们除了关心它的点估计外,有时还需要…
python 实现 AIGC 大模型中的概率论:生日问题的基本推导
在上一节中,我们对生日问题进行了严谨的阐述:假设屋子里面每个人的生日相互独立,而且等可能的出现在一年 365 天中的任何一天,试问我们需要多少人才能让某两个人的生日在同一天的概率超过 50%。
处理抽象逻辑问题的一个入手点就是…
如何理解《注意力机制真的懂得“集中注意力”吗?》
在文章《从熵不变性看Attention的Scale操作》中,我们就从“集中注意力”的角度考察过Attention机制,当时我们以信息熵作为“集中程度”的度量,熵越低,表明Attention越有可能集中在某个token上。 但是,对于一般的Attent…
n维随机变量、n维随机变量的分布函数
设随机试验E的样本空间是,其中表示样本点。
设是定义在上的随机变量,由它们构成一个n维向量,叫做n维随机向量,也叫n维随机变量。 对于任意n个实数,n元函数 称为n维随机变量的分布函数,也叫联合分布函数。
概率论中的 50 个具有挑战性的问题 [第 6 部分]:Chuck-a-Luck
一、说明 我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克莫斯特勒(Frederick Mosteller)的《概率论中的五十个具有挑战性的问题与解决方案》)一书。我认为创建一个系列来讨论这些可能作为面试问题出现的迷人问题会很有趣。每篇…
概率论1:下象棋问题(3.5)
每日小语
时刻望着他人的眼色行事,是腾飞不了的。自己怎么想就积极地去做,这是需要胆量的。——广中平佑 题目
甲、乙二人下象棋, 每局甲胜的概率为a,乙胜的概率为b. 为简化问题,设没有和局的情况,这意味着a b1. 设想…
概率统计Python计算:单因素试验参数的区间估计
对单因素试验模型X{X1,X2,⋯,Xs}X\{X_1,X_2,\cdots,X_s\}X{X1,X2,⋯,Xs},其中Xi{Xi1,Xi2,⋯,Xini}X_i\{X_{i1},X_{i2},\cdots,X_{in_i}\}Xi{Xi1,Xi2,⋯,Xini},i1,2⋯,si1,2\cdots,si1,2⋯,s(诸nin_ini未必相等)…
概率统计Python计算:自定义分布的方差计算
对于自定义分布,则可根据方差的计算公式,先分别计算出XXX的1阶原点矩E(X)E(X)E(X)和2阶原点矩E(X2)E(X^2)E(X2),然后计算D(X)E(X2)−[E(X)]2D(X)E(X^2)-[E(X)]^2D(X)E(X2)−[E(X)]2。 例1 设随机变量XXX的密度函数为f(x)12e−∣x∣,x∈(−∞,…
概率论基础——拉格朗日乘数法
概率论基础——拉格朗日乘数法
概率论是机器学习和优化领域的重要基础之一,而拉格朗日乘数法与KKT条件是解决优化问题中约束条件的重要工具。本文将简单介绍拉格朗日乘数法的基本概念、应用以及如何用Python实现算法。
1. 基本概念
拉格朗日乘数法是一种用来求解…
[概率论]四小时不挂猴博士
贝叶斯公式是什么 贝叶斯公式是概率论中的一个重要定理,用于计算在已知一些先验信息的情况下,更新对事件发生概率的估计。贝叶斯公式的表达式如下: P(A|B) P(B|A) * P(A) / P(B) 其中,P(A|B)表示在事件B发生的条件下事件A发生的概…
人工智能教程(四):概率论入门
目录 前言
TensorFlow 入门
SymPy 入门
概率论入门 前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。 点击跳转到网站 在本系列的 上一篇文章 中,我们进一步讨论了矩阵和线性代数&#…
技术学习|CDA level I 描述性统计分析(数据的描述性统计分析)
技术学习|CDA level I 描述性统计分析(数据的描述性统计分析)
数据的描述性统计分析常从数据的集中趋势、离散程度和分布形态3个方面进行。
一、集中趋势
集中趋势是指数据向其中心值靠拢的趋势。测量数据的集中趋势,主要是寻找其中心值。…
机器学习——贝叶斯分类器(基础理论+编程)
目录
一、理论
1、初步引入
2、做简化
3、拉普拉斯修正
二、实战
1、计算P(c)
2、计算P(x|c)
3、实战结果
1、数据集展示
2、相关信息打印 一、理论
1、初步引入
在所有相关概率都已知的理想情形下,贝叶斯决策论考虑如何基于这些概率和误判损失来选择最…
概率论与数理统计————1.随机事件与概率
一、随机事件
随机试验:满足三个特点
(1)可重复性:可在相同的条件下重复进行
(2)可预知性:每次试验的可能不止一个,事先知道试验的所有可能结果
(3)不确定…
概率论与数理统计————3.随机变量及其分布
一、随机变量
设E是一个随机试验,S为样本空间,样本空间的任意样本点e可以通过特定的对应法则X,使得每个样本点都有与之对应的数对应,则称XX(e)为随机变量 二、分布函数
分布函数:设X为随机变量…
整理了一下常用的LaTeX数学公式语法,未完待续
为了方便对应,后面会拆一下
公式代码放入LaTeX编译环境中时,两边需要加入$$:
$$公式代码$$ 1,分解示例
L^{A}T_{E}X\,2_{\epsilon} c^{2}a^{2}b^{2} \tau\phi \cos2\pi1 f\, \,a^{x}\,\,b \heartsuit \cos^{2}\theta \sin^{2}\theta 1.0…
BGV/BFV 的统一自举算法
参考文献:
[GV23] Geelen R, Vercauteren F. Bootstrapping for BGV and BFV Revisited[J]. Journal of Cryptology, 2023, 36(2): 12.Bit Extraction and Bootstrapping for BGV/BFV 文章目录 Bootstrapping for BGV and BFVDecryption FunctionBGVBFV Bootstrapp…
趣学贝叶斯统计:量化
概率理论不仅仅是一个数学概念,更是一种对随机性和不确定性的理解方式。通过量化我们对事件发生的信念,我们能够更准确地预测和解释各种现象。在本章中,我们将探讨事件概率与信念概率,为我们的理论和分析工具箱增添新的维度。
事…
武忠祥2025高等数学,基础阶段的百度网盘+视频及PDF
考研数学武忠祥基础主要学习以下几个方面的内容:
1.微积分:主要包括极限、连续、导数、积分等概念,以及它们的基本性质和运算方法。
2.线性代数:主要包括向量、向量空间、线性方程组、矩阵、行列式、特征值和特征向量等概念,以及它们的基本…
《机器人SLAM导航核心技术与实战》第1季:第7章_SLAM中的数学基础
视频讲解 【第1季】7.第7章_SLAM中的数学基础-视频讲解 【第1季】7.1.第7章_SLAM中的数学基础_SLAM发展简史-视频讲解 【第1季】7.2.第7章_SLAM中的数学基础_SLAM中的概率理论-视频讲解 【第1季】7.3.第7章_SLAM中的数学基础_估计理论-视频讲解 【第1季】7.4.第7章_SLAM中的…
人工智能之估计量评估标准及区间估计
评估估计量的标准 无偏性:若估计量( X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn)的数学期望等于未知参数θ,即 E ( θ ^ ) = θ E(\hat\theta)=\theta E(θ^)=θ 则称 θ ^ \hat\theta θ^为θ的无偏估计量。 估计量 θ ^ \hat\theta θ^的值不一定就是…
概率论与数理统计实验 附源码及实验报告 可打包为exe
👋 Hi, I’m 货又星👀 I’m interested in …🌱 I’m currently learning …💞 I’m looking to collaborate on …📫 How to reach me … README 目录(持续更新中) 各种错误处理、爬虫实战及模…
联合概率分布-概率质量函数归一化性质-连续型变量概率分布
更多AI技术入门知识与工具使用请看下面链接: https://student-api.iyincaishijiao.com/t/iNSVmUE8/
趣学贝叶斯统计:条件概率(1)
前言
到目前为止,我们只讨论了独立事件的概率。当一个事件的结果不影响另一个事件的结果时,这两个事件就是独立事件。例如,掷硬币时出现正面并不影响掷骰子是否会掷出6点。计算独立事件的概率要比计算非独立事件的概率容易得多,但…
【初中生讲机器学习】12. 似然函数和极大似然估计:原理、应用与代码实现
创建时间:2024-02-23 最后编辑时间:2024-02-24 作者:Geeker_LStar 你好呀~这里是 Geeker_LStar 的人工智能学习专栏,很高兴遇见你~ 我是 Geeker_LStar,一名初三学生,热爱计算机和数学,我们一起加…
概率基础——多元正态分布
概率基础——多元正态分布
介绍
多元正态分布是统计学中一种重要的多维概率分布,描述了多个随机变量的联合分布。在多元正态分布中,每个随机变量都服从正态分布,且不同随机变量之间可能存在相关性。本文将以二元标准正态分布为例࿰…
python计算重要概率分布
目录 1、伯努利分布
2、二项分布
3、负二项分布
4、几何分布
5、泊松分布
6、均匀分布
7、贝塔分布
8、正态分布
9、指数分布
10、卡方分布 1、伯努利分布
伯努利分布(Bernoulli Distribution)是一种离散型概率分布,又被称为0-1分布…
例解变分自编码器(VAE)
本文通过一个回归例子介绍变分自编码器。产生训练和测试样本的代码如下:
# data
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inlinedef f(x, sigma):# y 10 * sin(2 * pi) epsilonreturn 10 * np.sin(2 * np.pi *…
概率论与数理统计 第一章 概率论的基本概念
文章目录 第一章 概率论的基本概念1.1 随机试验1.1.1 前言1.1.2 随机试验 1.2 样本空间、随机事件1.2.1 样本空间1.2.2 随机事件1.2.3 事件的关系、事件的运算、运算法则1.2.3.1 事件的关系1.2.3.2 事件的运算1.2.3.3 运算法则 1.3 频率与概率1.3.1 概率的描述性定义1.3.2 概率…
EM算法:数学推导+实例演示
EM(Expectation Maximum)算法即期望最大化算法,是一种对不完全数据(因数据缺失或有未被观测等含有隐变量的数据)估计未知变量的迭代算法。
在隐变量这篇文章里用一个例子解释了什么是隐变量,本文会在此例基础上进行扩展来引出EM算法是什么、能解决什么问题以及是如何解决问题…
贝尔曼方程【Bellman Equation】
强化学习笔记 主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程,个人觉得赵老师的课件深入浅出,很适合入门.
第一章 强化学习基本概念 第二章 贝尔曼方程 文章目录 强化学习笔记一、状态值函数贝尔曼方程二、贝尔曼方程的向量形式三、动作值…
matlab概率论例子
高斯概率模型:
[f,xi] ksdensity(x): returns a probability density estimate, f, for the sample in the vector x.
The estimate is based on a normal kernel function, and is evaluated at 100 equally spaced points, xi, that cover the range of the da…
108、3D Gaussian Splatting for Real-Time Radiance Field Rendering
简介
官网 更少训练时间的同时实现最先进的视觉质量,能在1080p分辨率下实现高质量的实时(≥30 fps)新视图合成
NeRF使用隐式场景表示,体素,点云等属于显示建模方法,3DGS就是显示辐射场。它用3D高斯作为灵活高效的表示方法&…
概率论与数理统计-第7章 假设检验
假设检验的基本概念
二、假设检验的基本思想
假设检验的基本思想实质上是带有某种概率性质的反证法,为了检验一个假设H0,是否正确,首先假定该假设H0正确,然后根据抽取到的样本对假设H0作出接受或拒绝的决策,如果样本观察值导致了…
DDPM中的 最优贝叶斯去噪(Optimal Bayesian Denoising)
最优贝叶斯去噪(Optimal Bayesian Denoising)是统计学中的一种方法,用于处理具有噪声的随机变量或数据。它的核心目标是从噪声数据中估计出最接近真实未受干扰数据的版本。这个方法基于贝叶斯统计理论,通过最小化均方误差…
《统计学简易速速上手小册》第6章:多变量数据分析(2024 最新版)
文章目录 6.1 主成分分析(PCA)6.1.1 基础知识6.1.2 主要案例:客户细分6.1.3 拓展案例 1:面部识别6.1.4 拓展案例 2:基因数据分析 6.2 聚类分析6.2.1 基础知识6.2.2 主要案例:市场细分6.2.3 拓展案例 1&…
概率基础——几何分布
概率基础——几何分布
介绍
在统计学中,几何分布是描述了在一系列独立同分布的伯努利试验中,第一次成功所需的试验次数的概率分布。在连续抛掷硬币的试验中,每次抛掷结果为正面向上的概率为 p p p,反面向上的概率为 1 − p 1-p …
趣学贝叶斯统计:概率密度分布(probability density function)
目录 1. 分布:PDF与PMFPDFPMF 2. 将概率密度函数应用于我们的问题用积分量化连续分布积分度量变化率:导数 3. R语言实践4. 小结 1. 分布:PDF与PMF
PDF
PDF定义在连续值上。在连续型随机变量的情况下,具体取某个数值的概率是0,因此PDF并不直…
贝叶斯统计——入门级笔记
绪论
1.1 引言
全概率公式 贝叶斯公式 三种信息
总体信息 当把样本视为随机变量时,它有概率分布,称为总体分布. 如果我们已经知道总体的分布形式这就给了我们一种信息,称为总体信息 样本信息 从总体中抽取的样本所提供的信息 先…
压缩感知常用的测量矩阵
测量矩阵的基本概念
在压缩感知(Compressed Sensing,CS)理论中,测量矩阵(也称为采样矩阵)是实现信号压缩采样的关键工具。它是一个通常为非方阵的矩阵,用于将信号从高维空间映射到低维空间&…
【概率论与数理统计】Chapter2 随机变量及其分布
随机变量与分布函数
随机变量
随机变量:一个随机变量是对随机现象可能的结果的一种数学抽象
分布函数
分布函数: X为随机变量, F ( x ) F(x) F(x)定义为: F ( x ) P ( X ≤ x ) F(x) P(X \leq x) F(x)P(X≤x) 定义域&#…
高创新!EI论文复现:计及源荷随机特性的综合能源系统/热电联供型微网优化运行程序代码!
适用平台:MatlabYalmipCplex
程序针对由风光机组、燃料/光伏电池、余热锅炉、燃气锅炉、蓄电池以及电/热负荷构成的热电联供型微网/综合能源系统,考虑风电、光伏功率以及热、电负荷的随机性,应用机会约束规划理论建立经济运行优化模型&#…
【概率论】中心极限定理(二)
文章目录 主观题主观题 每袋味精的净重为随机变量,平均重量为 100 克,标准差为 10 克。一箱内装 200 袋味精,求一箱味精的净重大于 20500 克的概率? 解: ① E ( X i ) = 100 , D ( X i ) = 1 0 2
概率与常见的概率分布
概率是数据分析、机器学习中最基础的知识。也是在生活中最实用的一门学科,学了很多大道理不一定能过好一生,学好概率则有一定概率会变得更好。为大概率坚持,为小概率备份。
概率与分布 要想了解概率,首先得搞清楚概率和概率分布的…
2023年考研计算机数学考什么?
不管是2022年考研还是2023年考研,计算机考研数学一般是数学一,考试题型主要是单选题、填空题和简答题。不同题型考查方向不一样,以下是小编搜集的考研计算机数学考试内容重点,可供2023年考研计算机数学备考使用。
一. 单选
选择…
概率论与数理统计:第二、三章:一维~n维随机变量及其分布
文章目录 Ch2. 一维随机变量及其分布1.一维随机变量1.随机变量2.分布函数 F ( x ) F(x) F(x)(1)定义(2)分布函数的性质 (充要条件)(3)分布函数的应用——求概率3.最大最小值函数 2.一维离散型随机变量及其概率分布(分布律)3.一维连续型随机变量及其概率分布(概率密度)4.一般类型…
SLAM 求解IPC算法
基础知识:方差,协方差,协方差矩阵 方差:描述了一组随机变量的离散程度 方差 每个样本值 与 全部样本的平均值 相差的平方和 再求平均数,记作: 例如:计算数字1-5的方差,如下 去中心化…
Redis中的HyperLogLog以及HyperLogLog原理
大家在学习redis的过程中,除了String,list,hash,set,zset这五种基本的数据结构,一定还会接触到几种高级的数据结构,比如bitmap,geo, 还有今天我们要说的hyperloglog&…
数模笔记15-马尔可夫算法
马尔可夫算法 随机过程 研究随机现象变化过程的概率规律性的学科。
定义1: 设{ξt,t∈T}是一族随机变量,T是一个实数集合,若对任意实数t∈T,ξt是一个随机变量,则称{ξt,t∈T}为随机过程。设\{…
小船过河问题解析(过度解析)
一开始输入一个数组a和一个数i(i代表人数)
然后用冒泡排序从小到大进行排列,存放在数组a中(按照从小到大的顺序进行排列的目的是为了两种解决方案的实行)
dp[i]中存放的数据代表的意思就是当有i个人过河时ÿ…

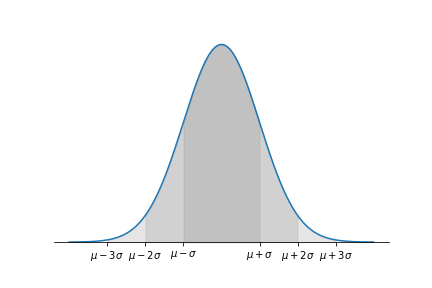







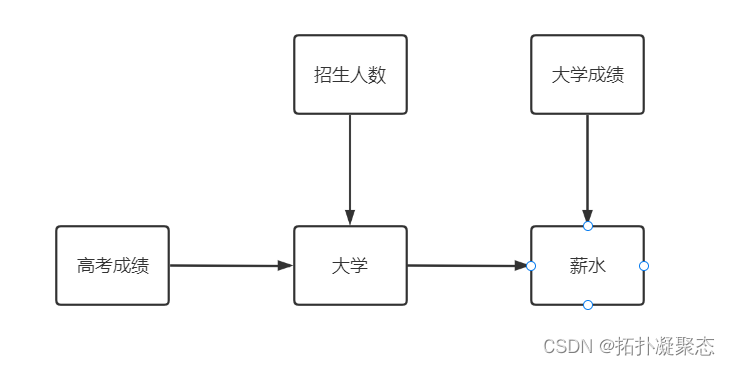









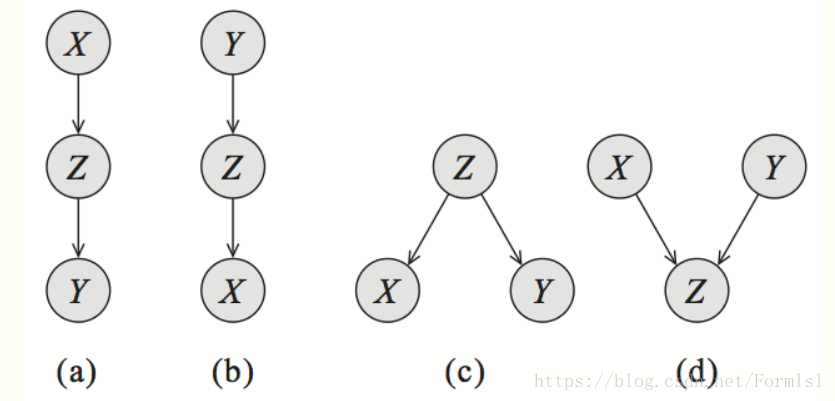
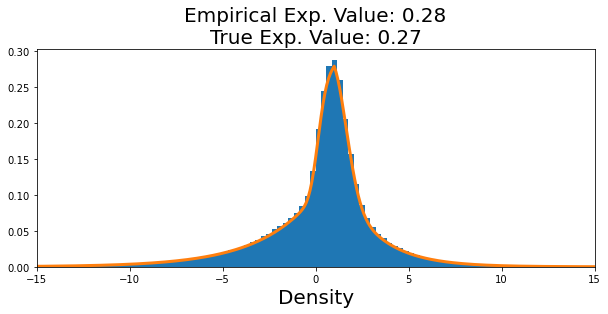

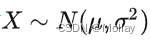
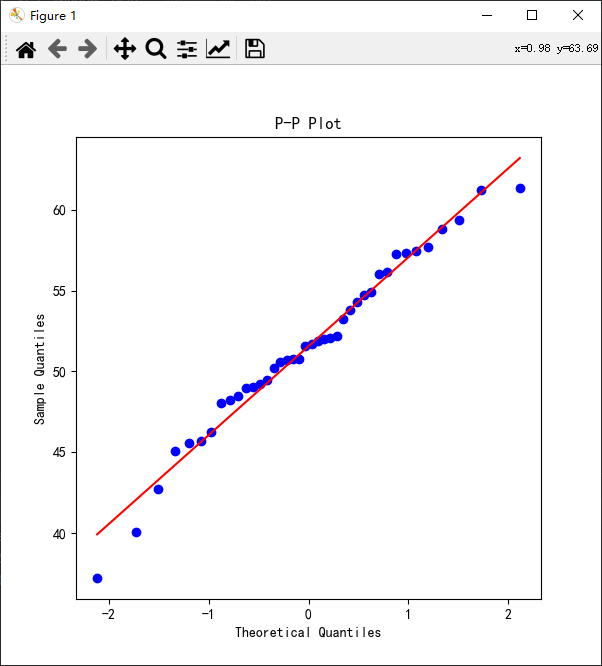

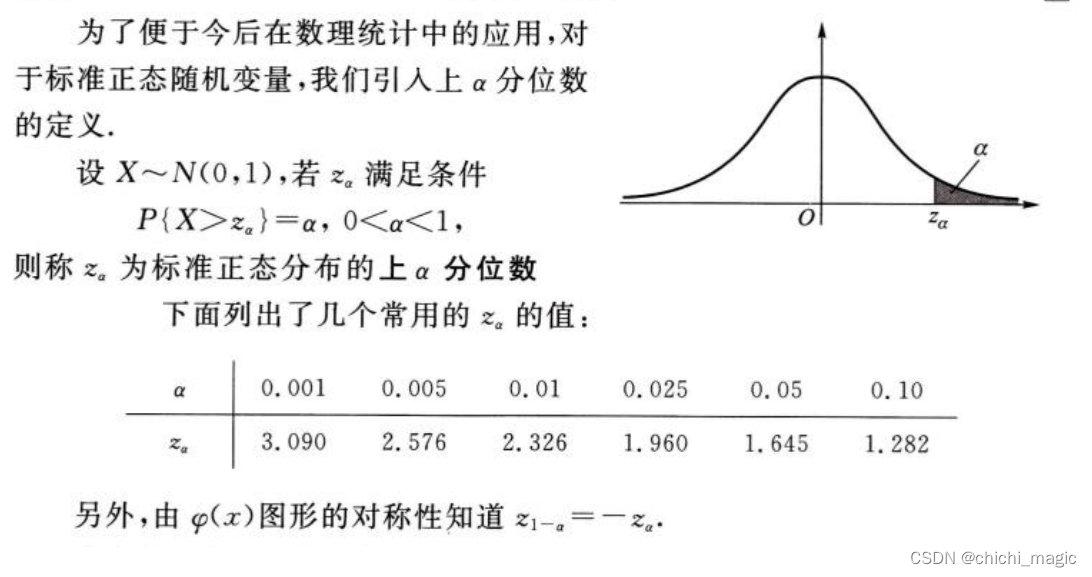











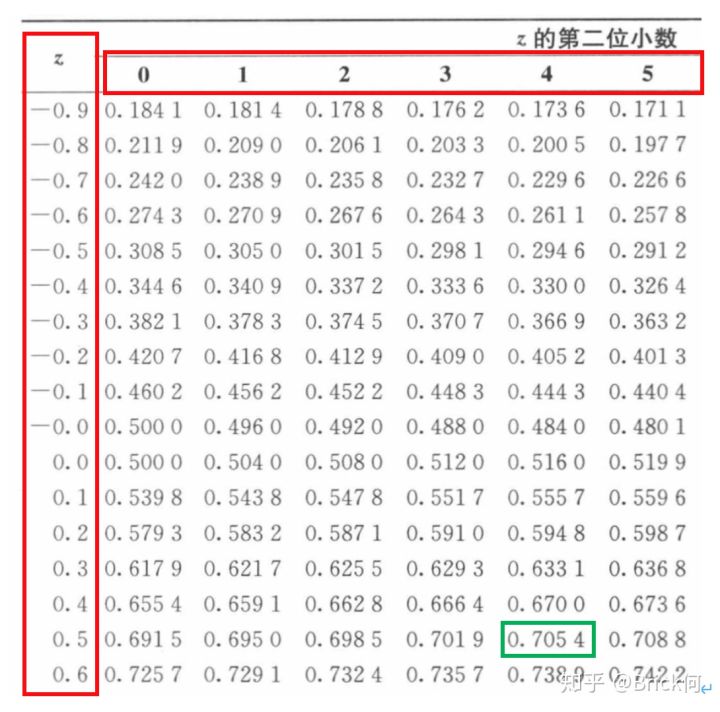






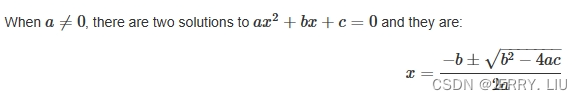
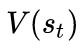
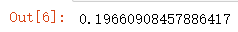


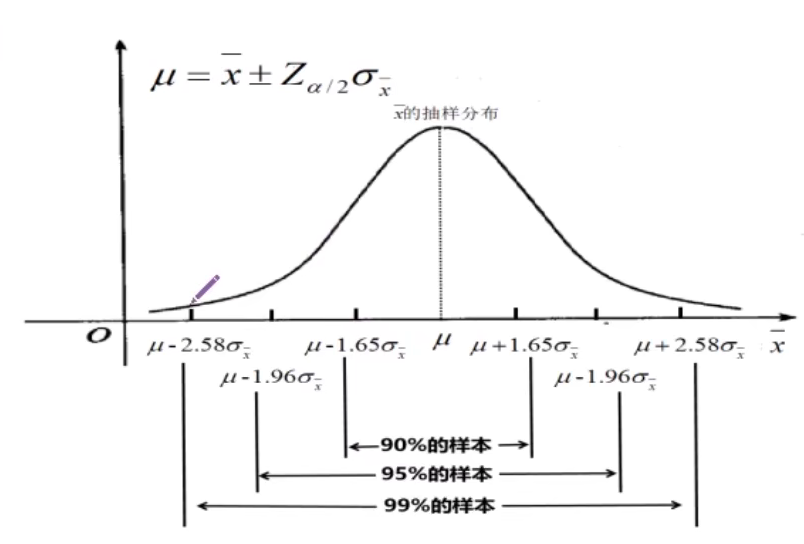



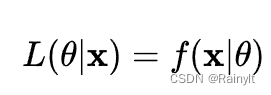






![[解题报告]《算法零基础100讲》(第1讲) 幂和对数](https://img-blog.csdnimg.cn/822e7a8a5ba24a148fb2c300dc6a6d1b.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAWGluZ2xlaUdhbw==,size_20,color_FFFFFF,t_70,g_se,x_16)
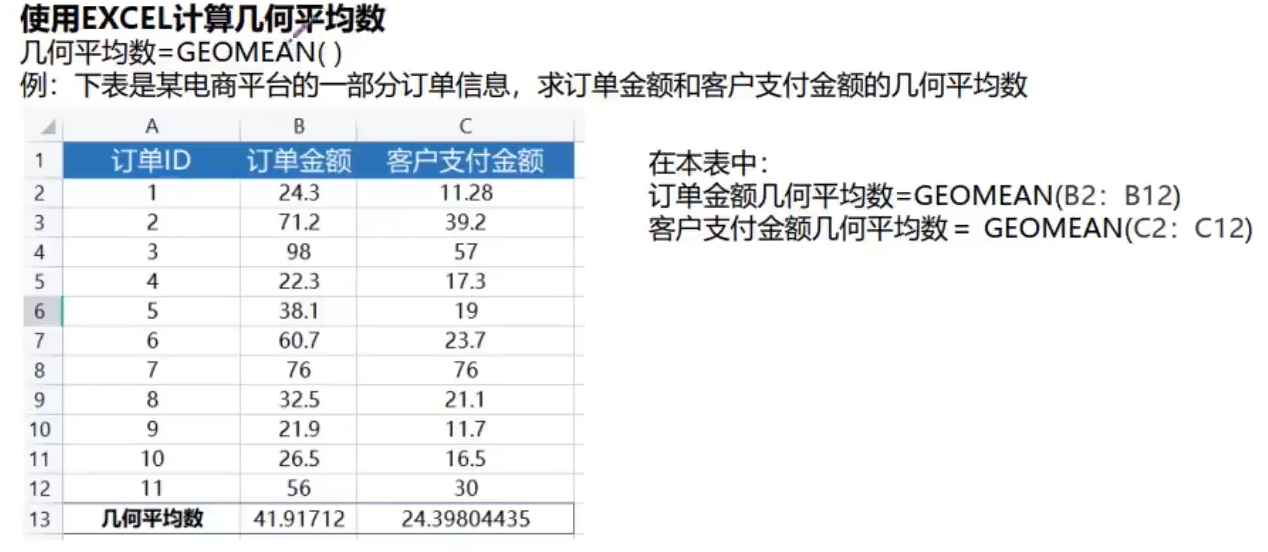
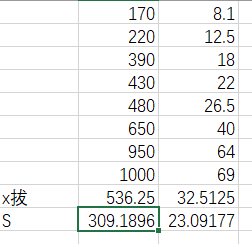
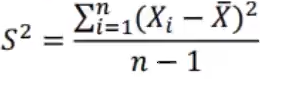
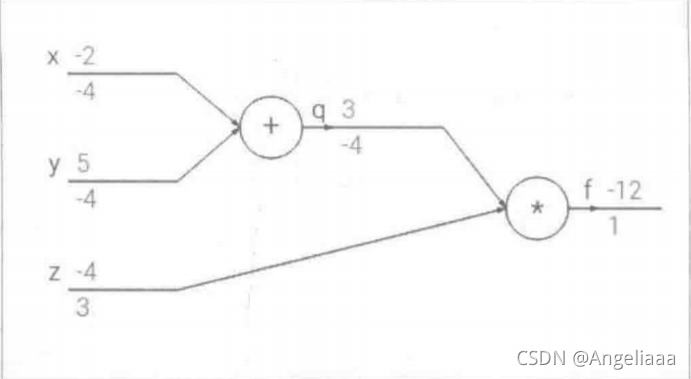
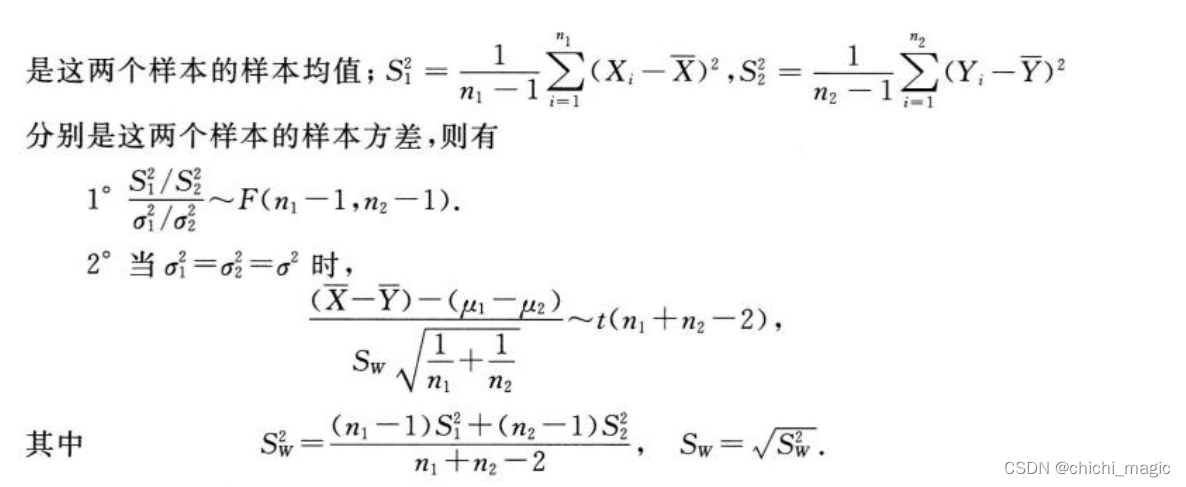
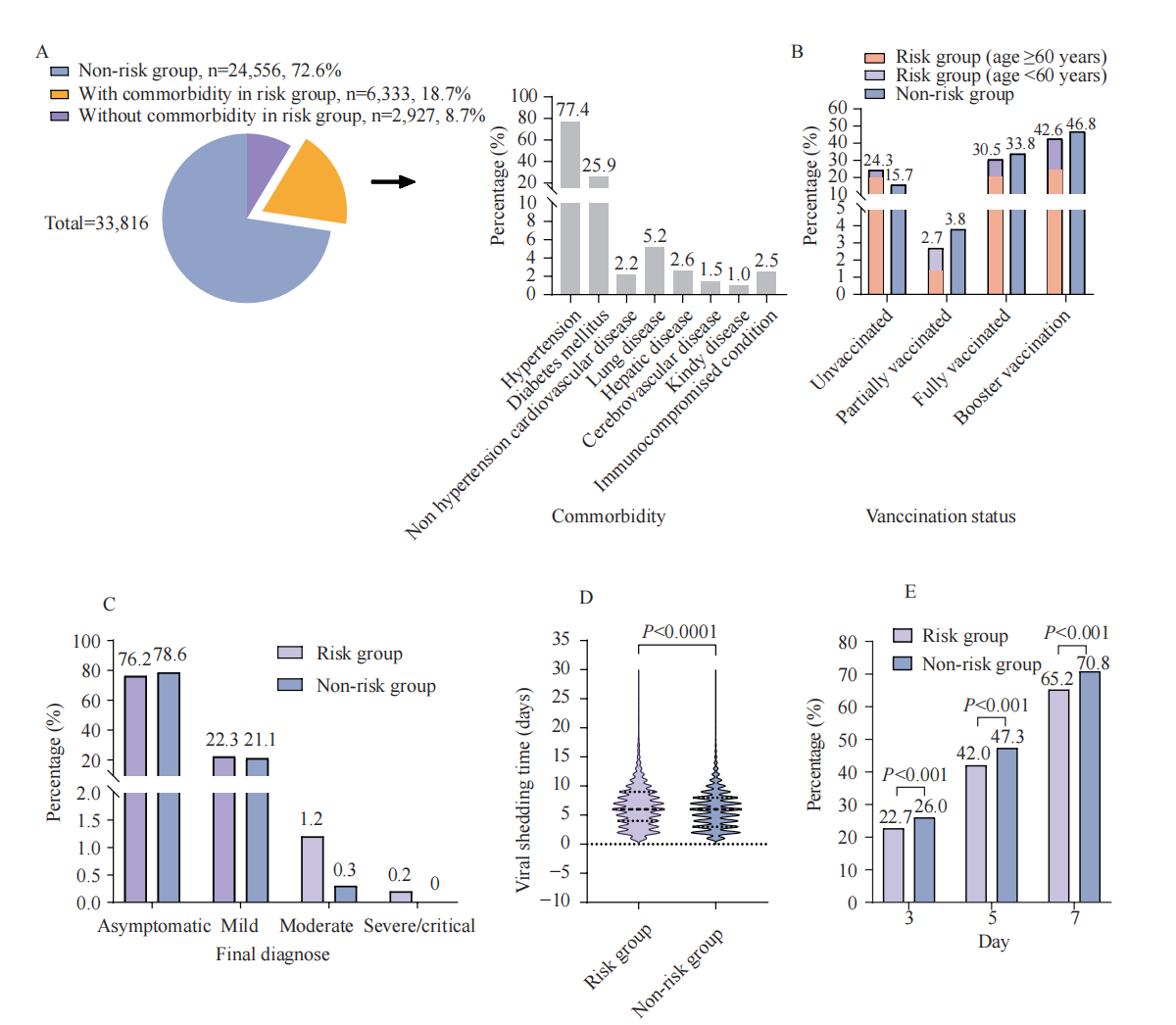
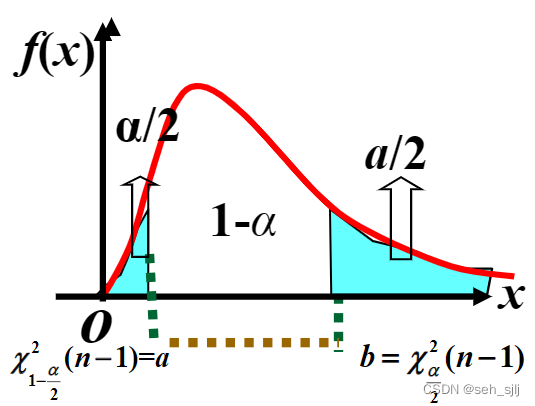
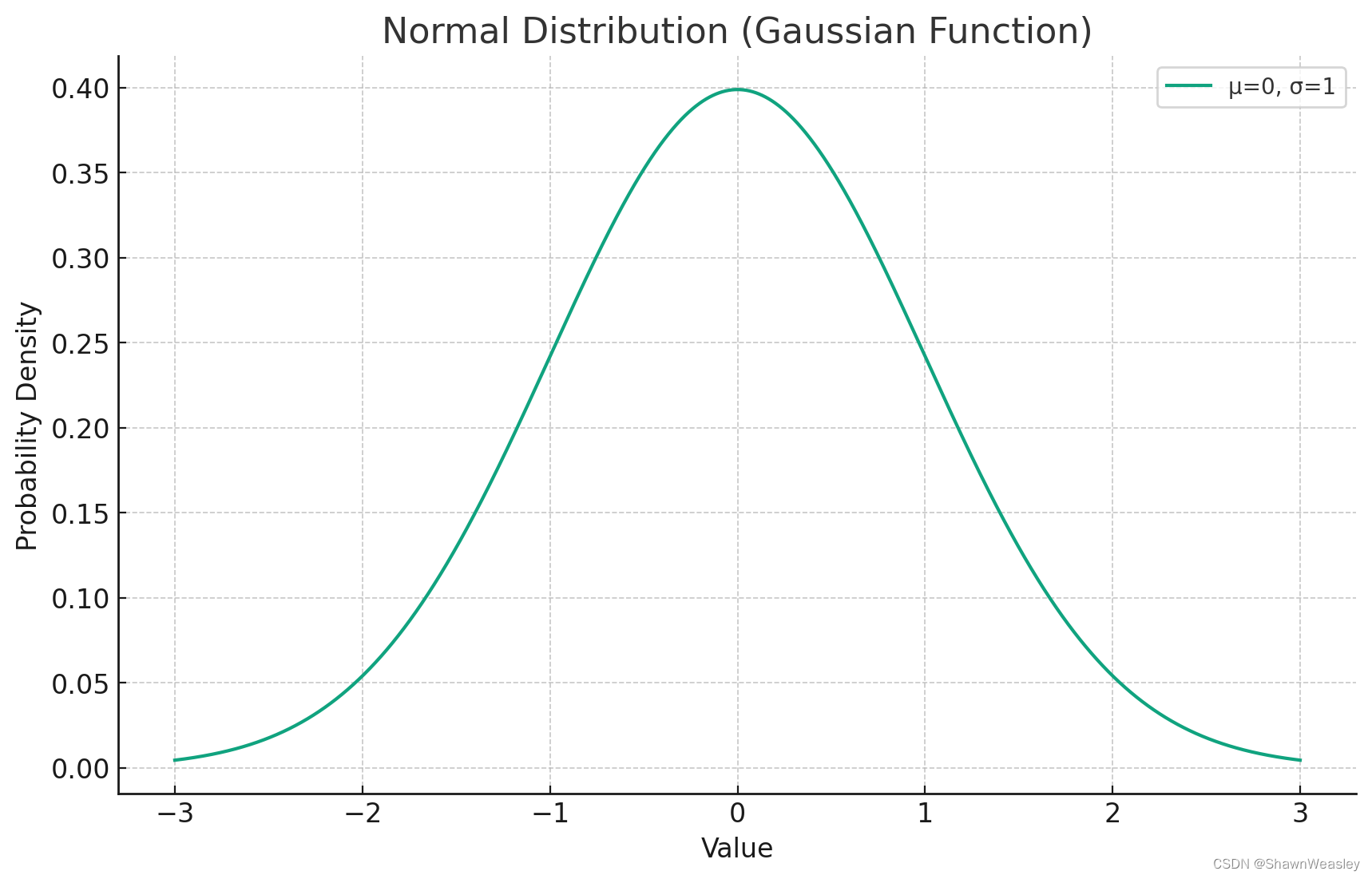






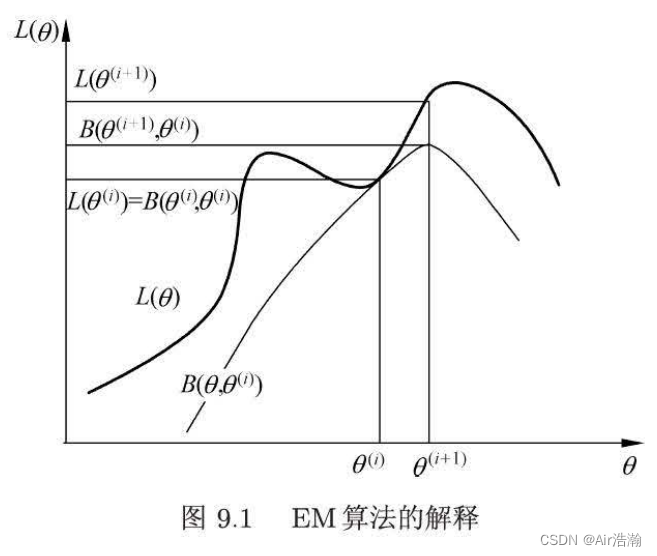
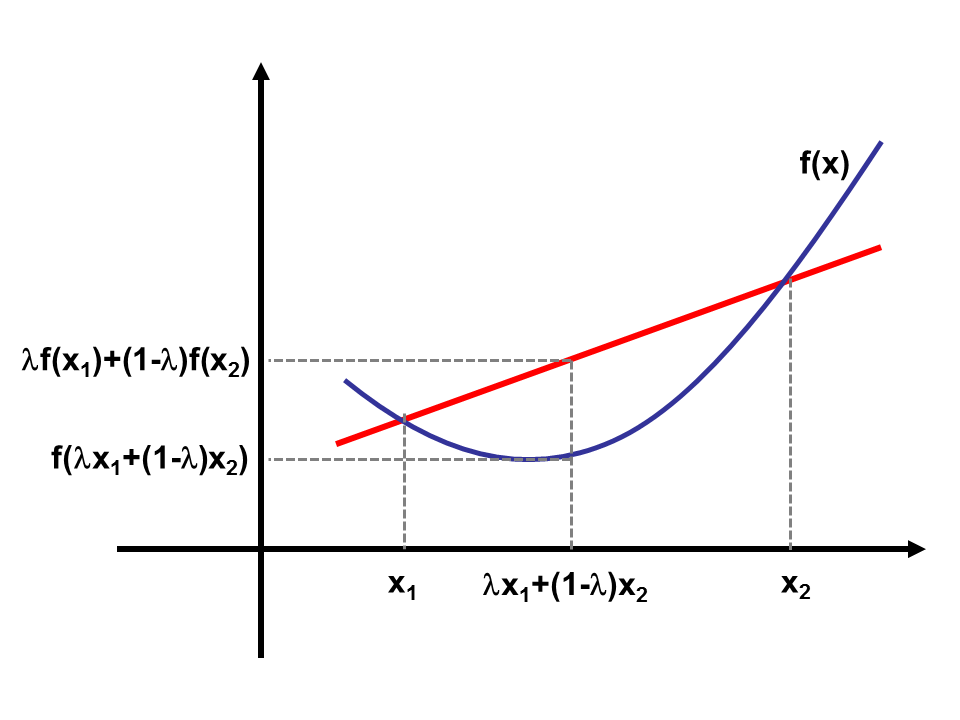








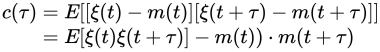
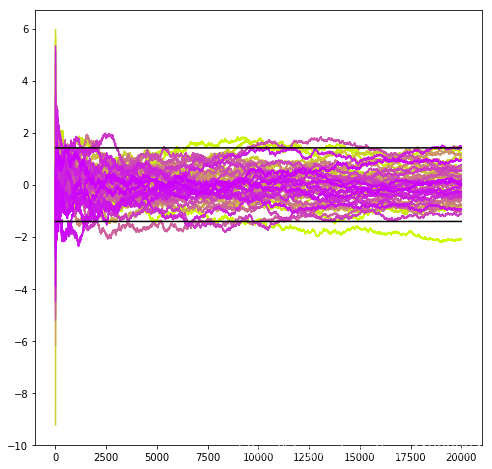




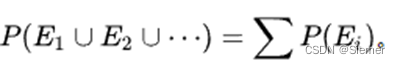

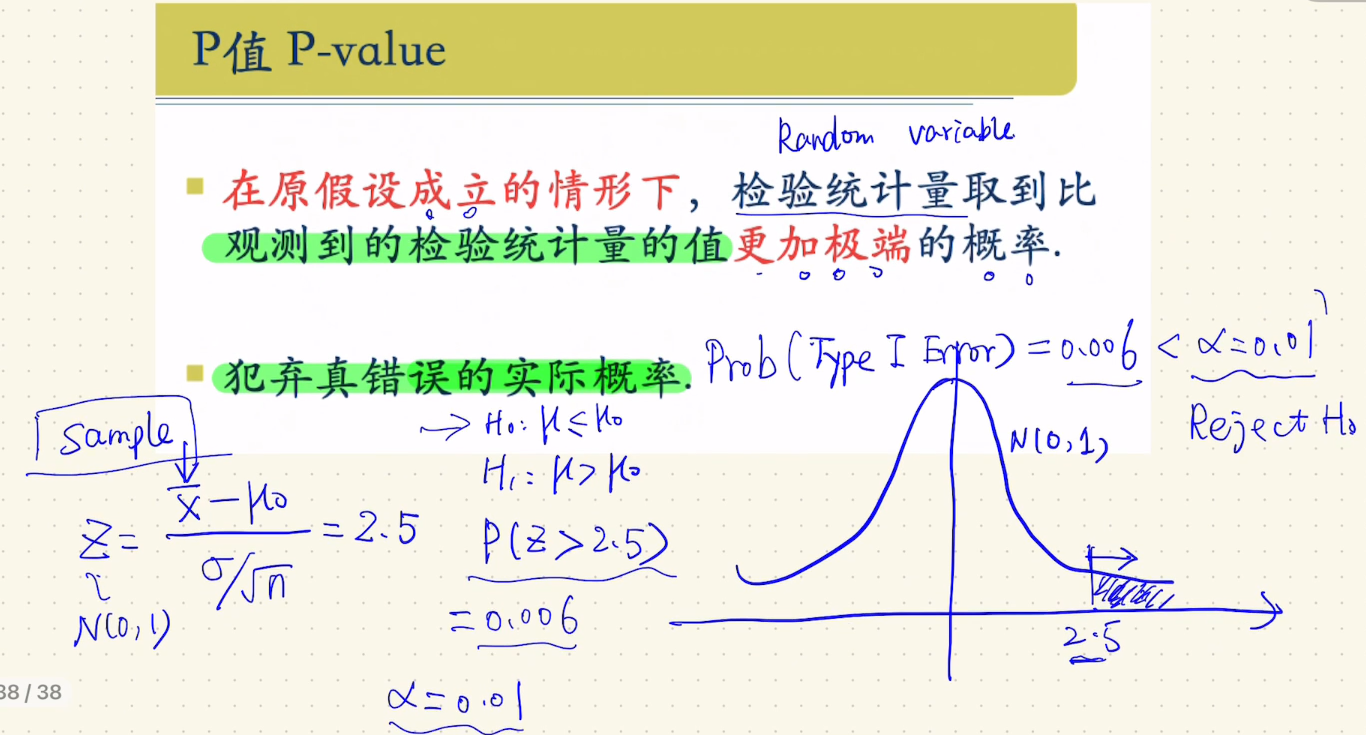

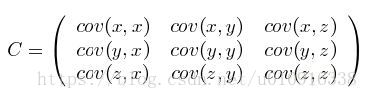


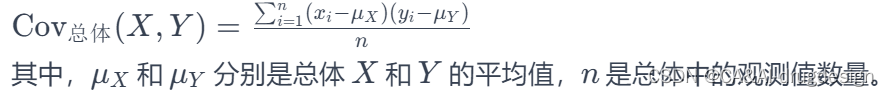

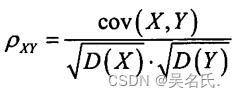

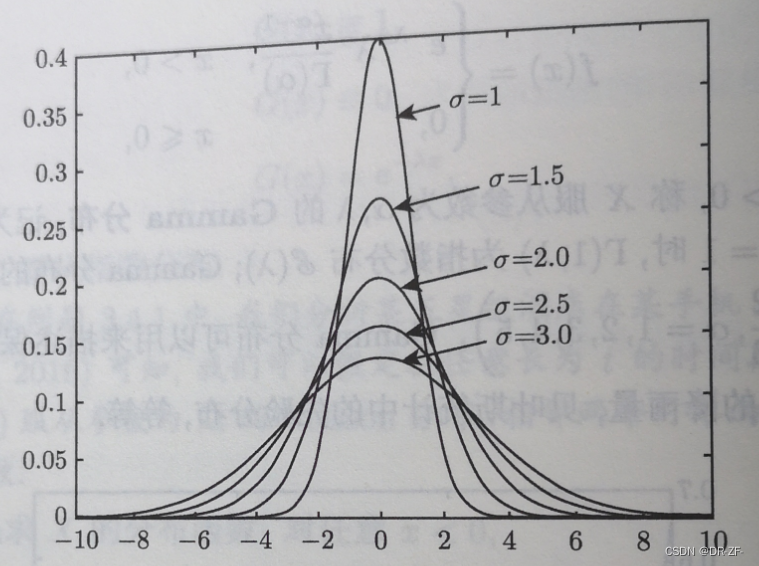


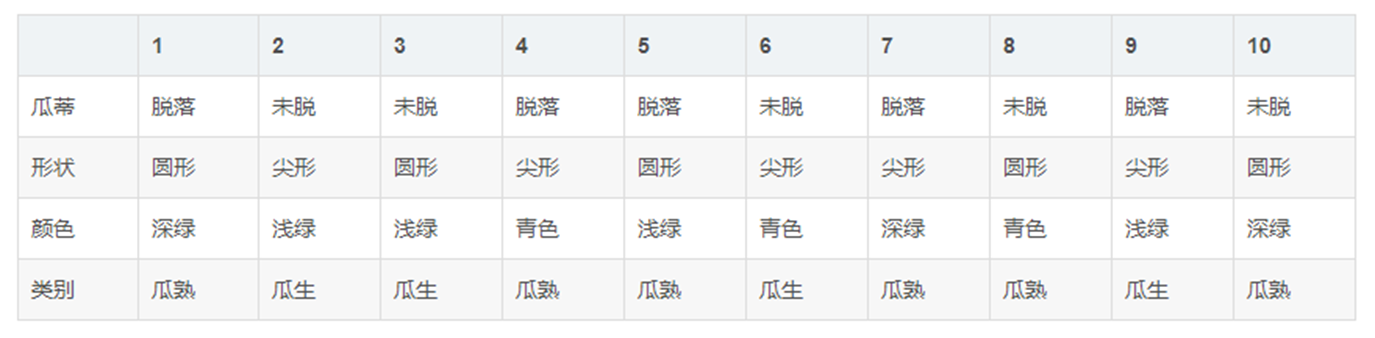



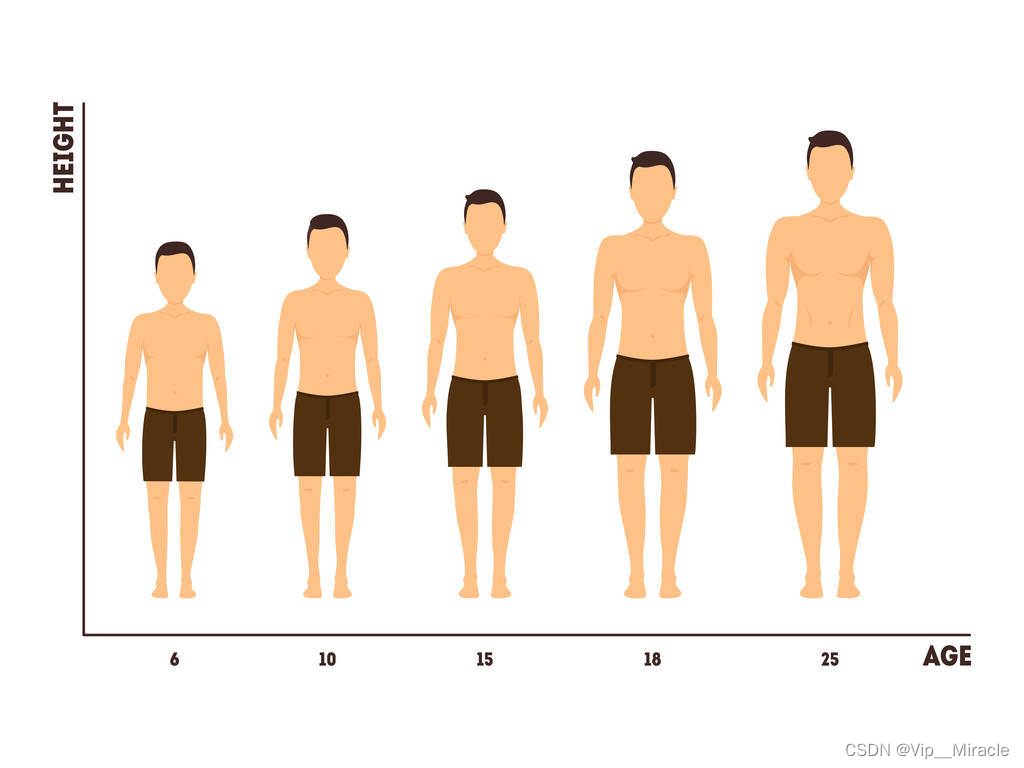




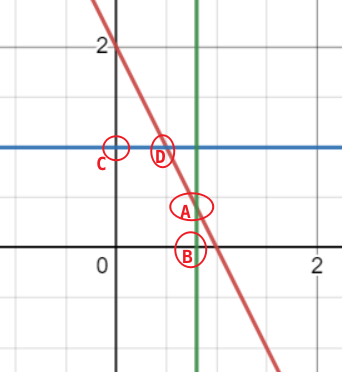



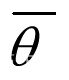






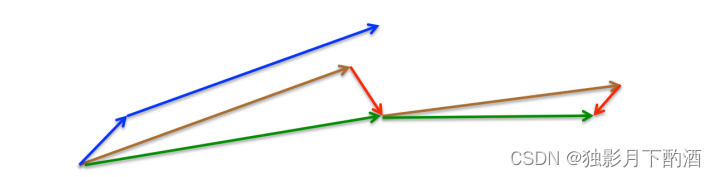


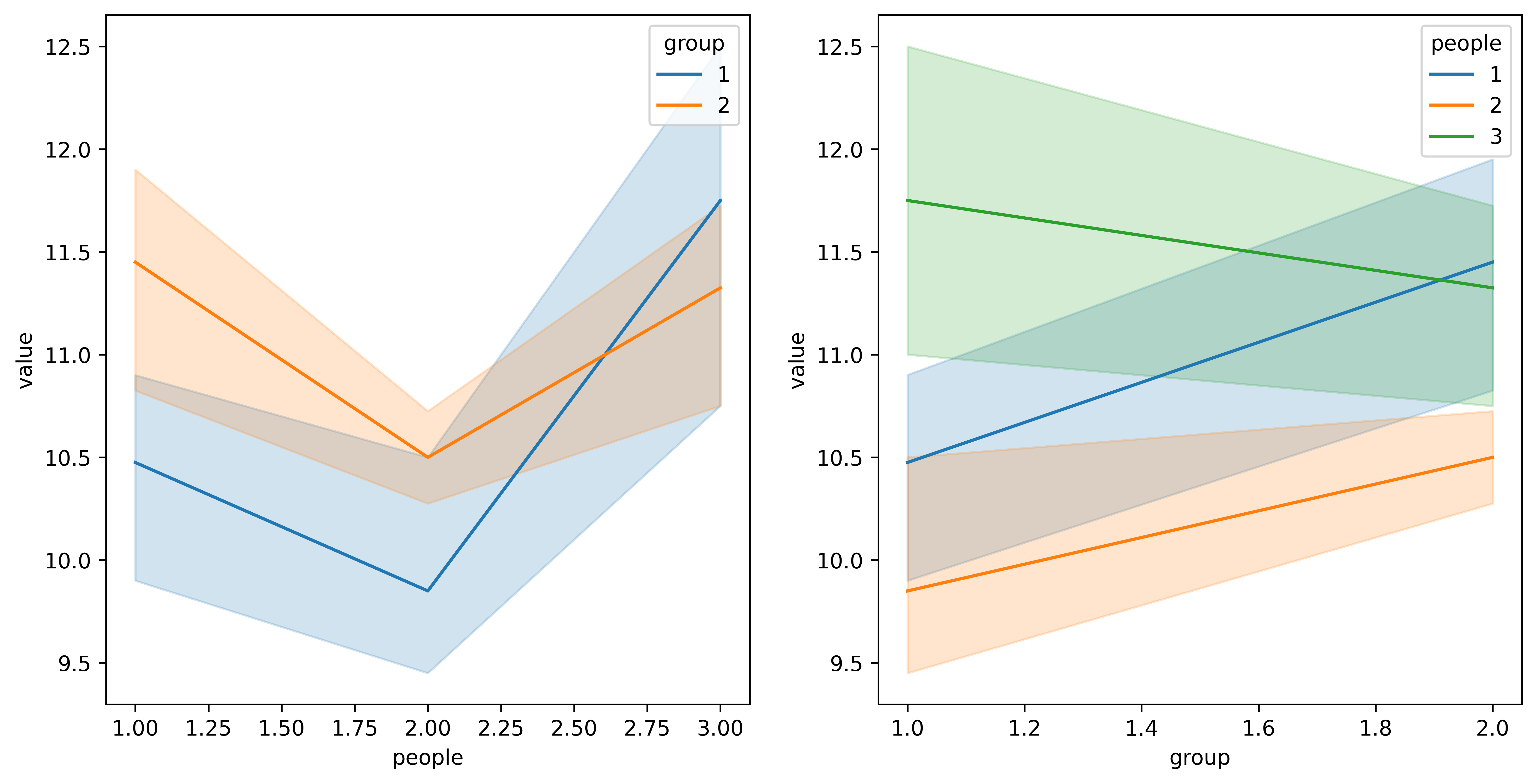

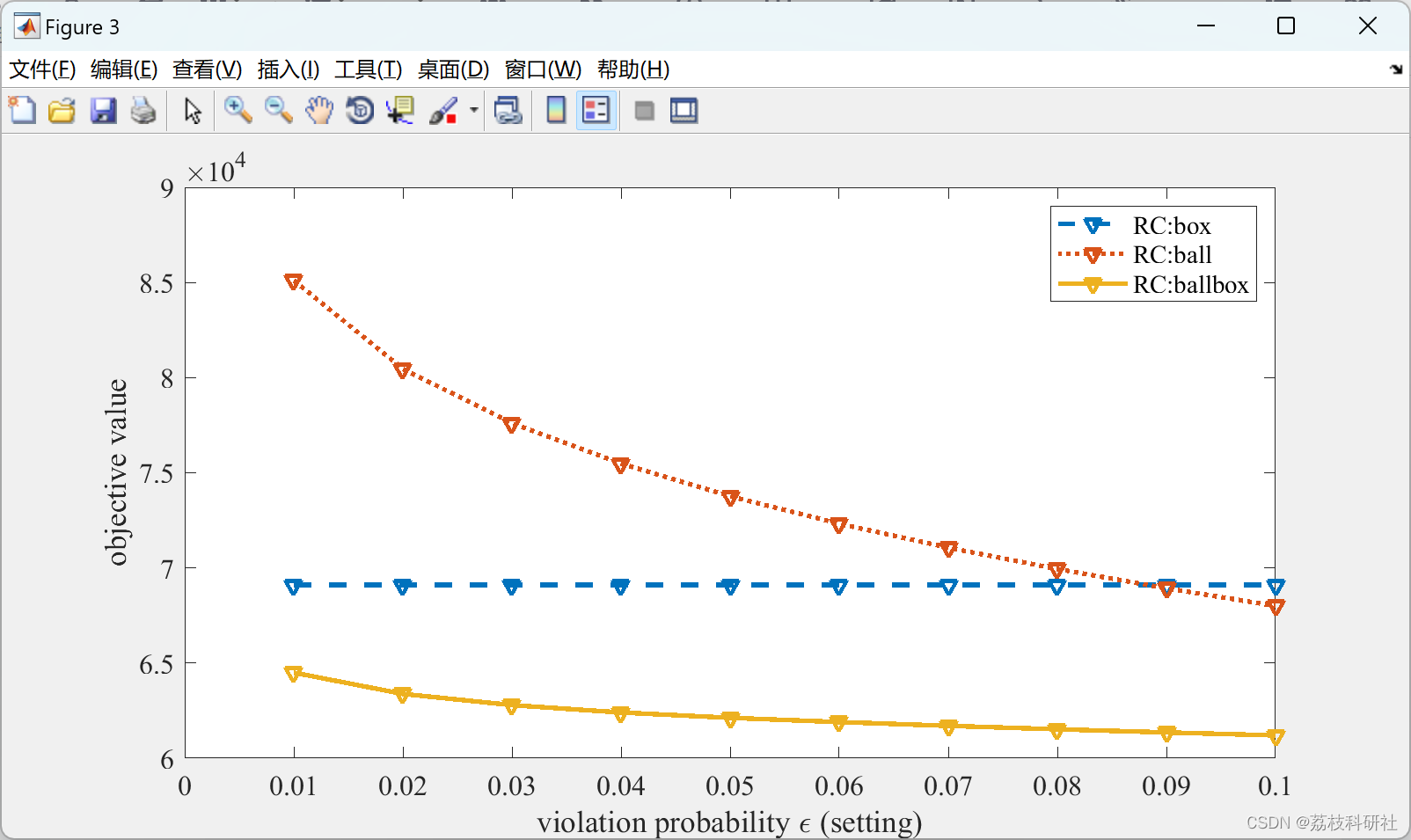
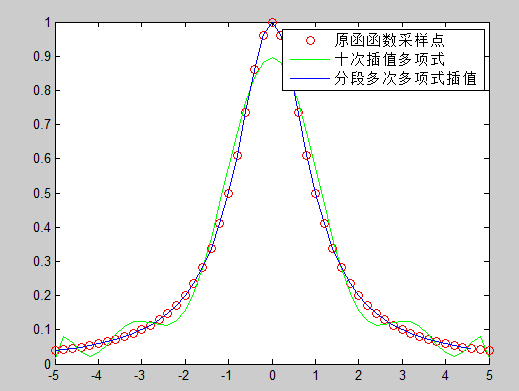


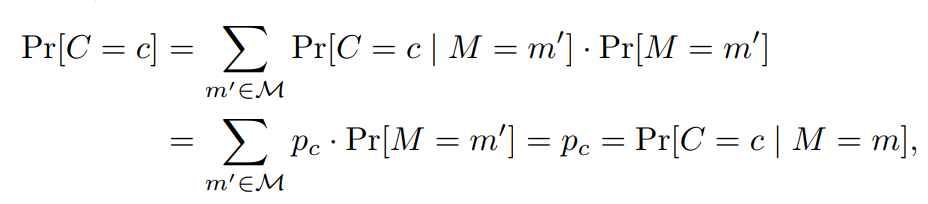
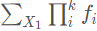

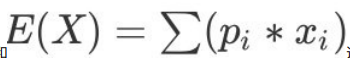
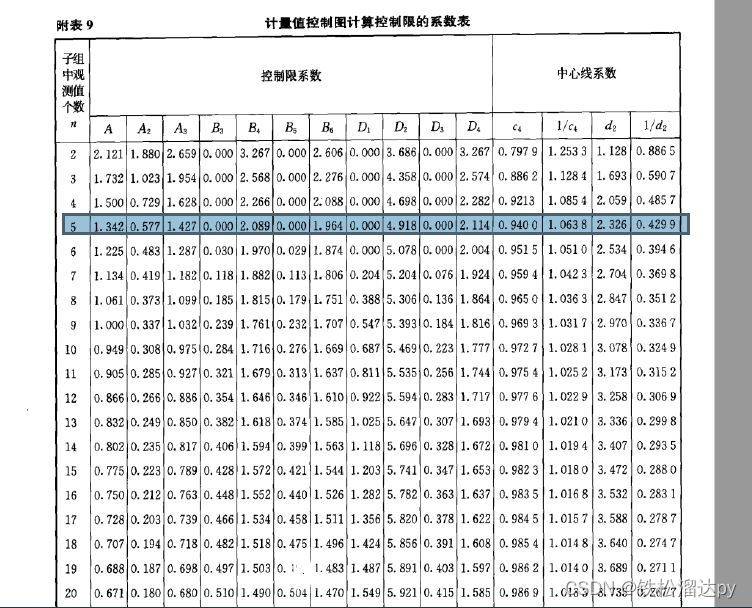

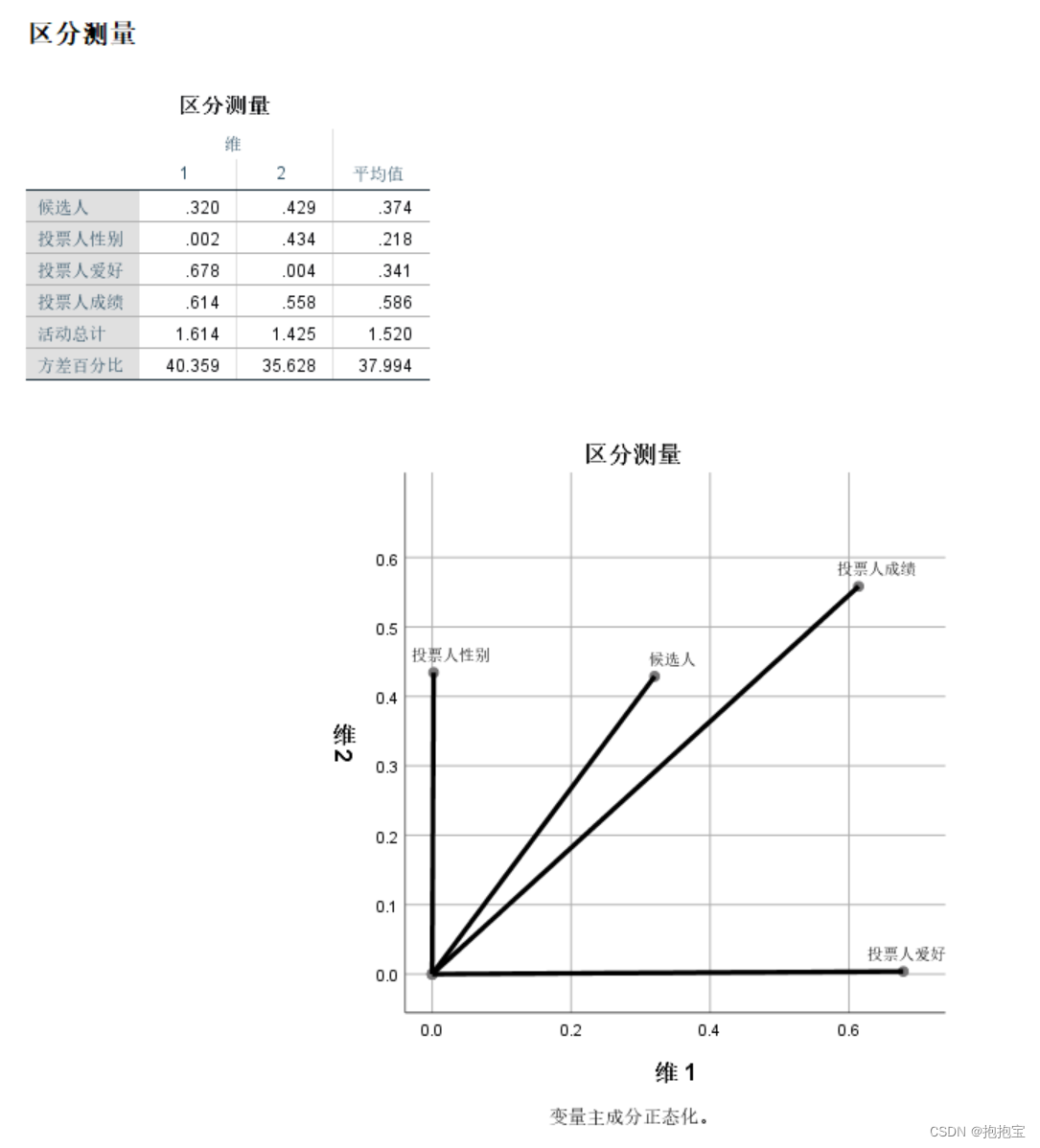
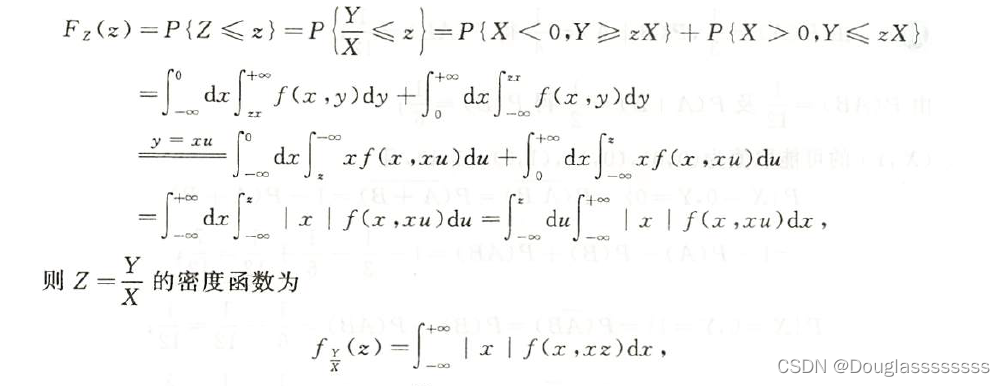
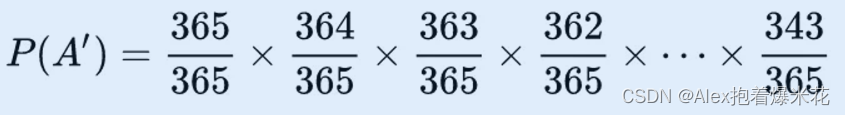
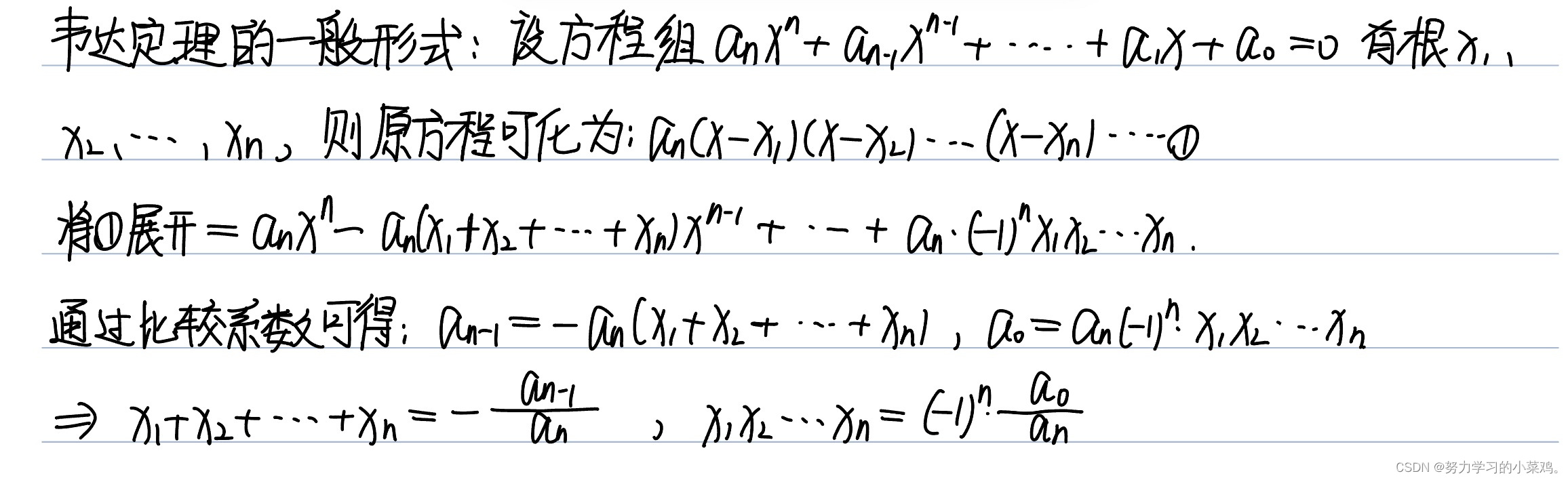



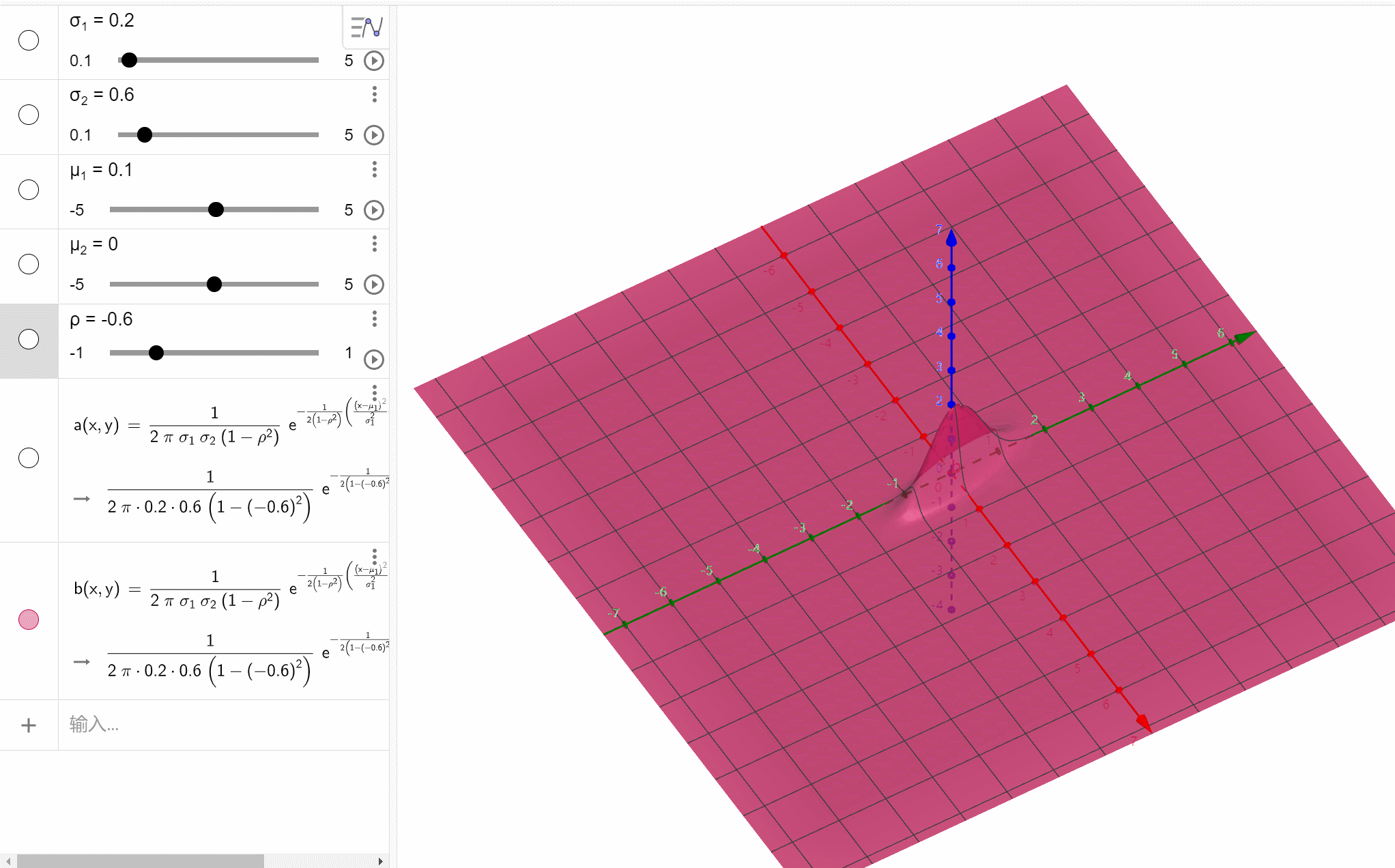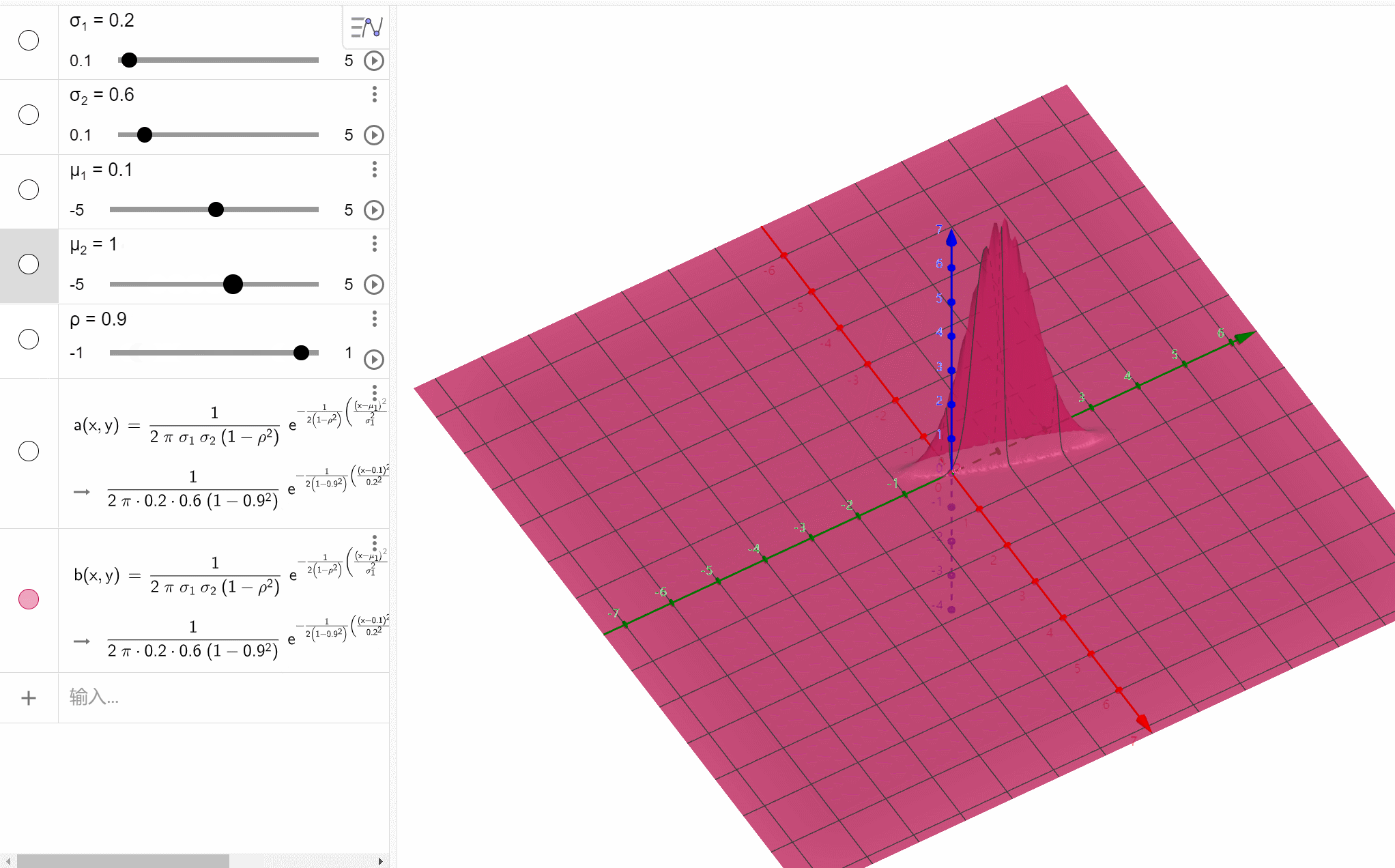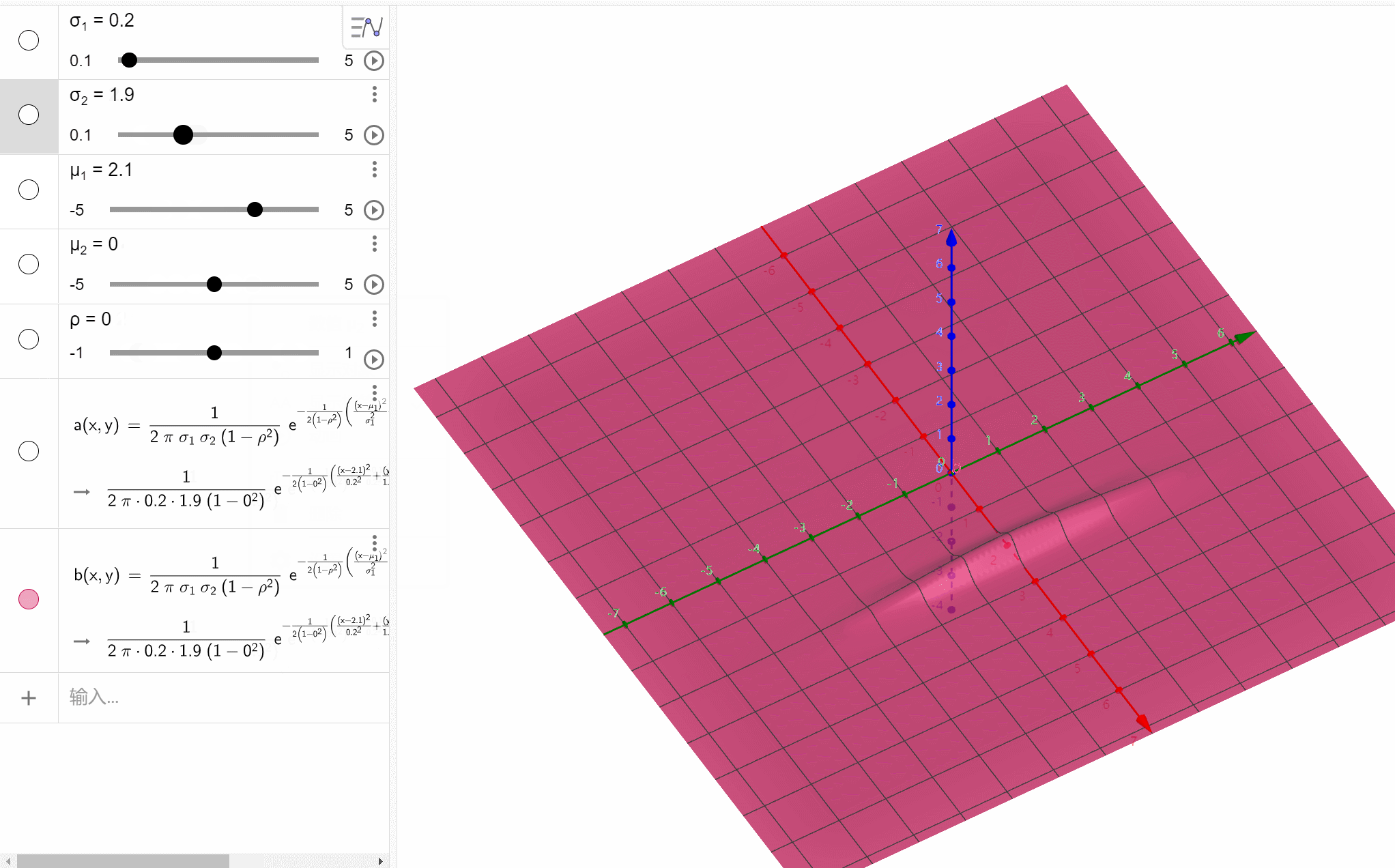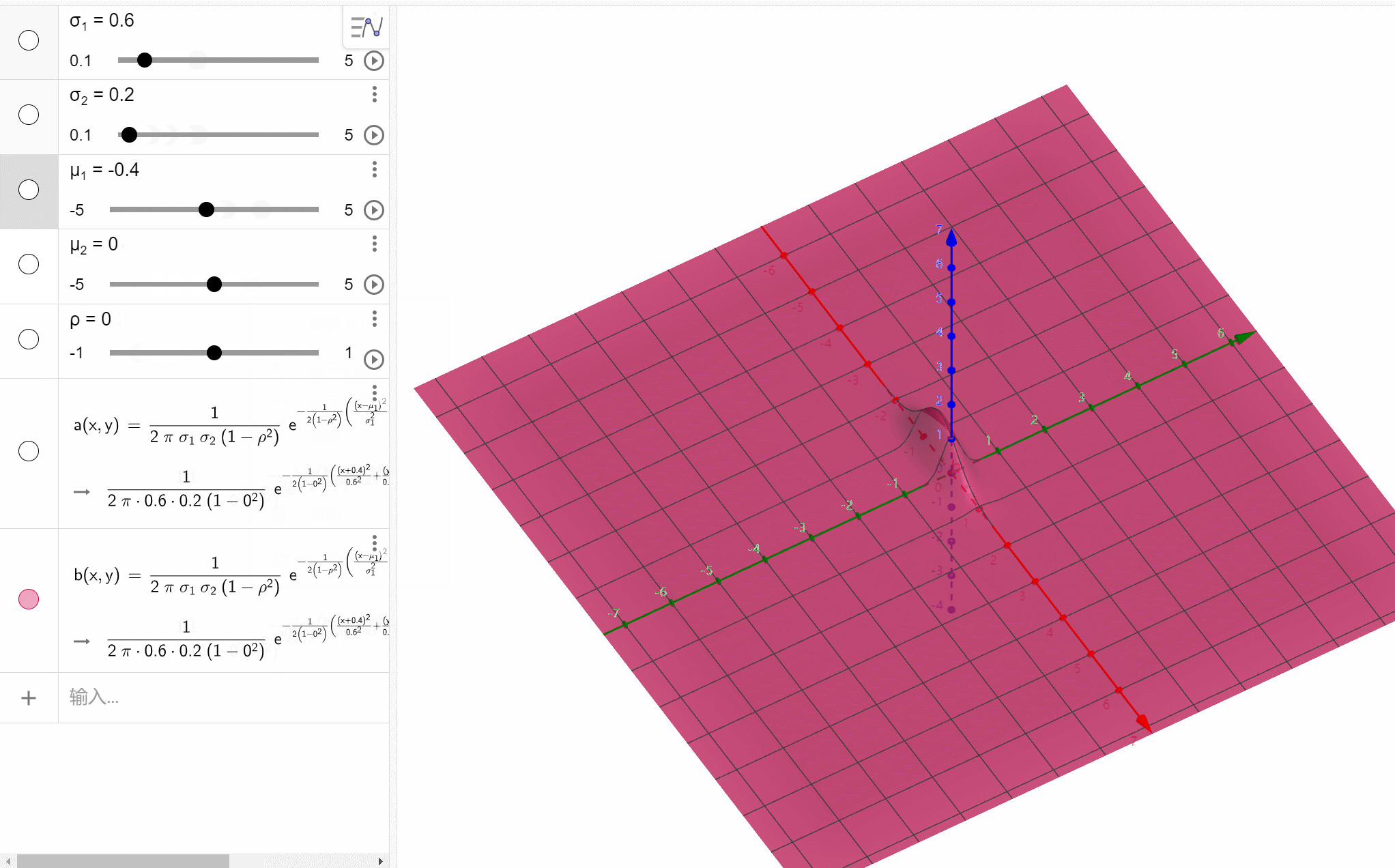
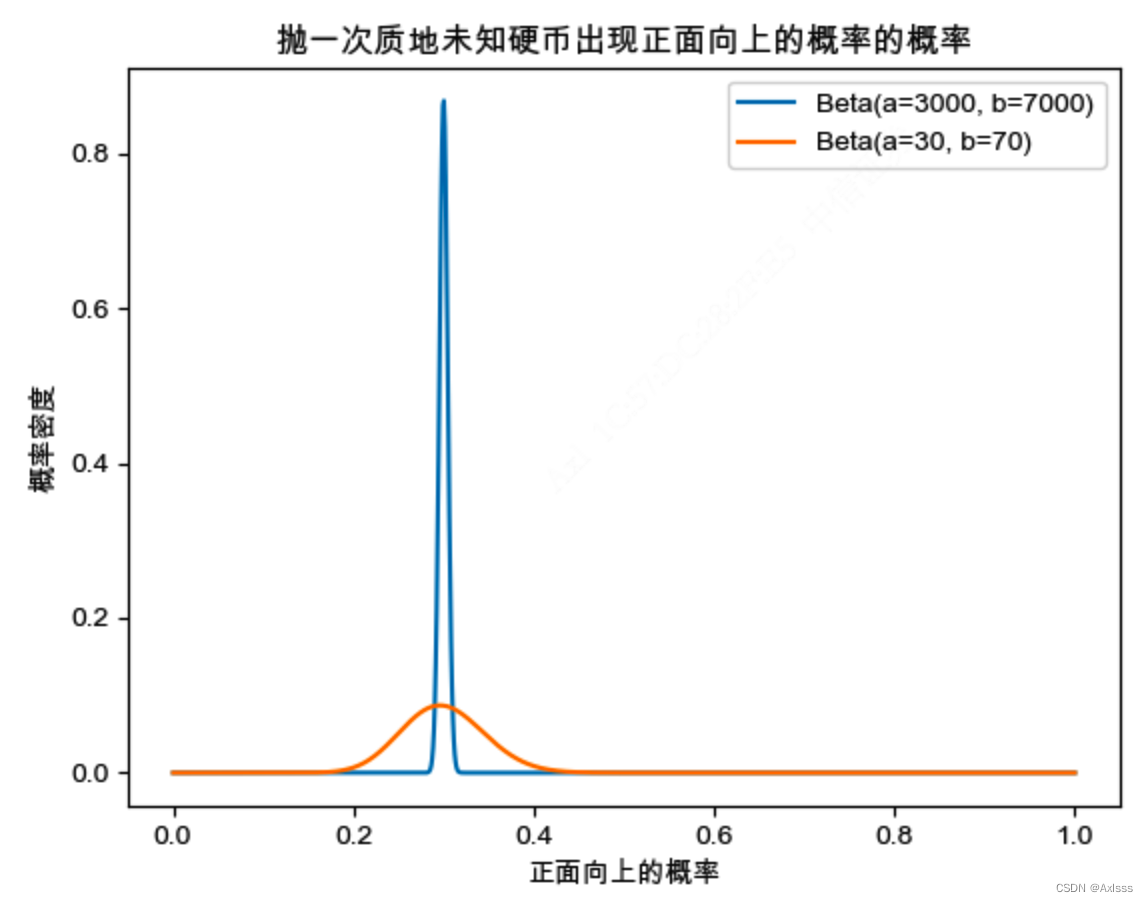
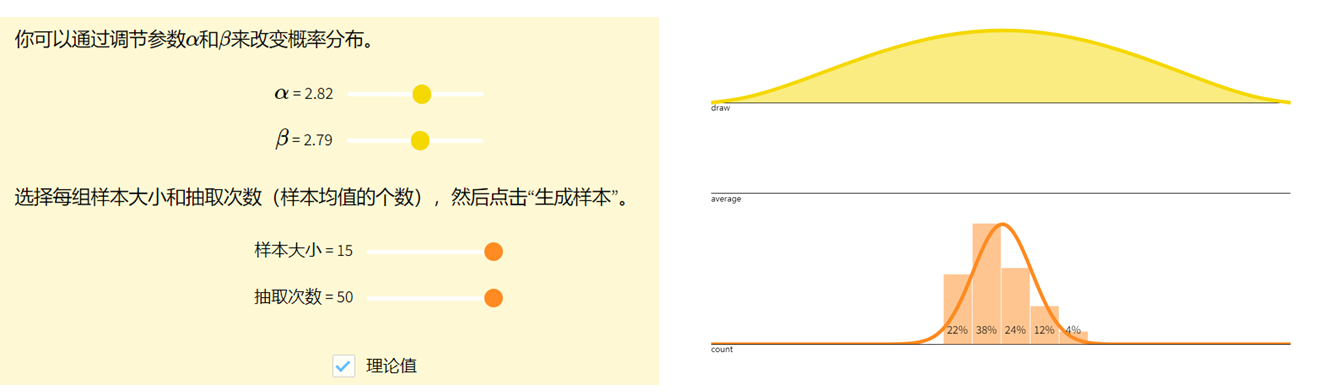


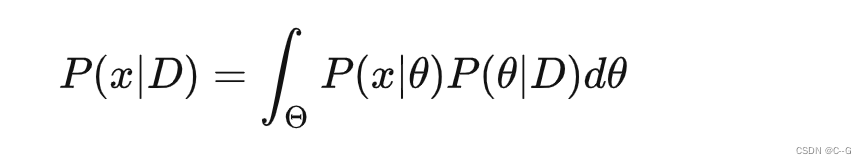




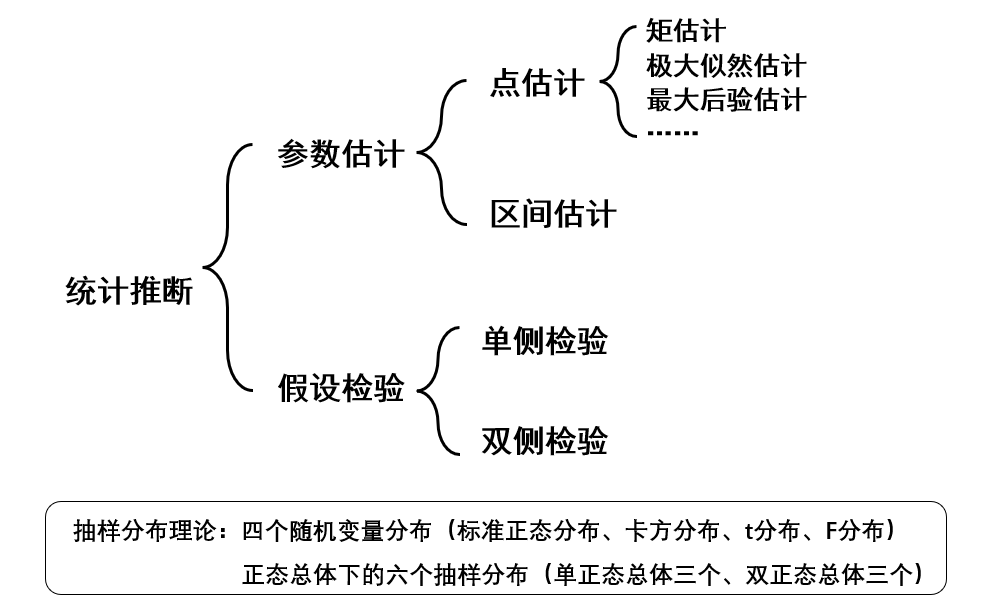
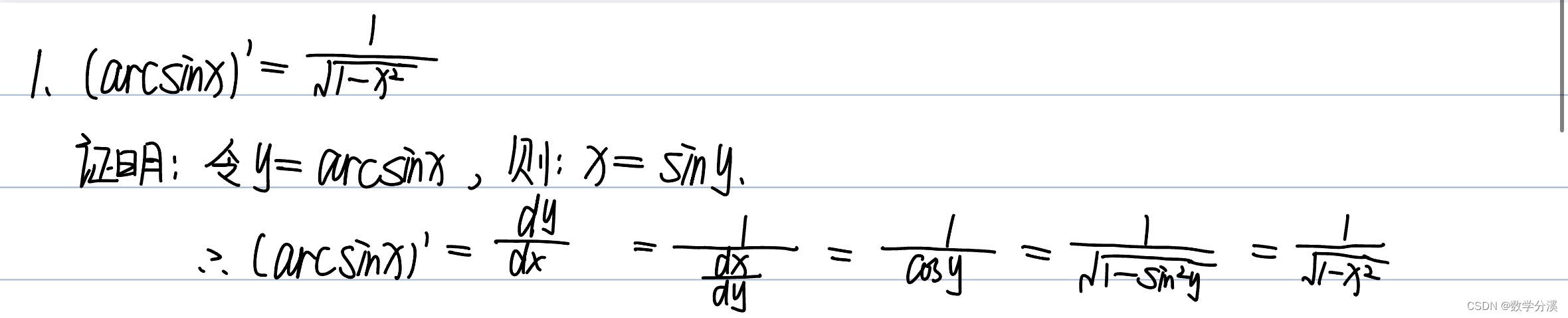




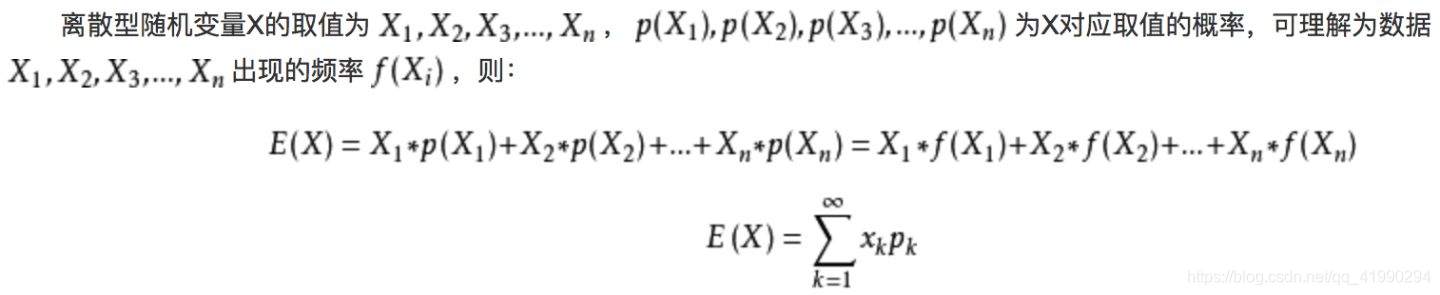
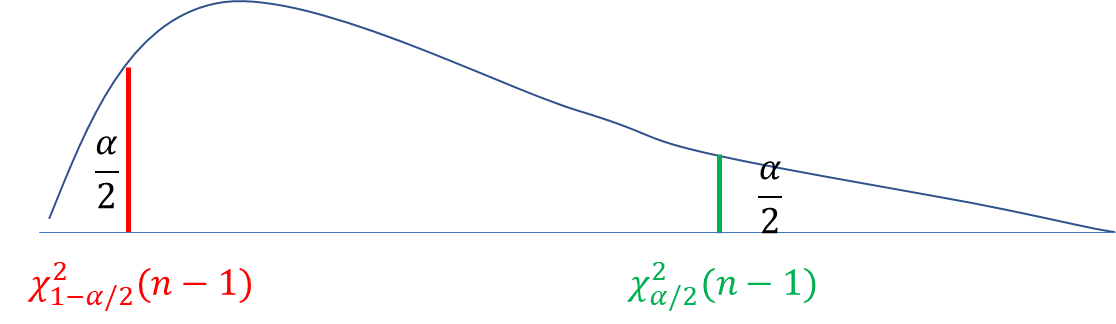


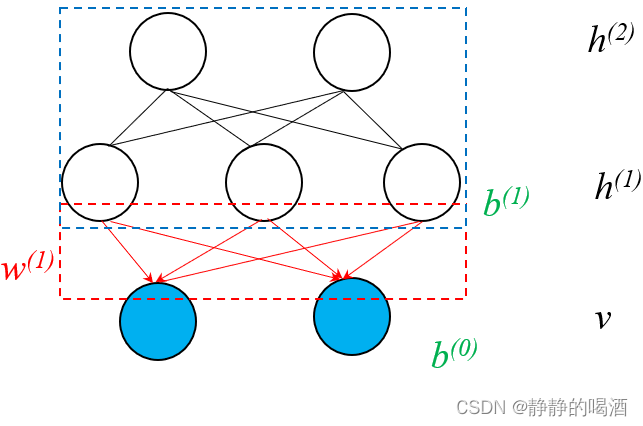
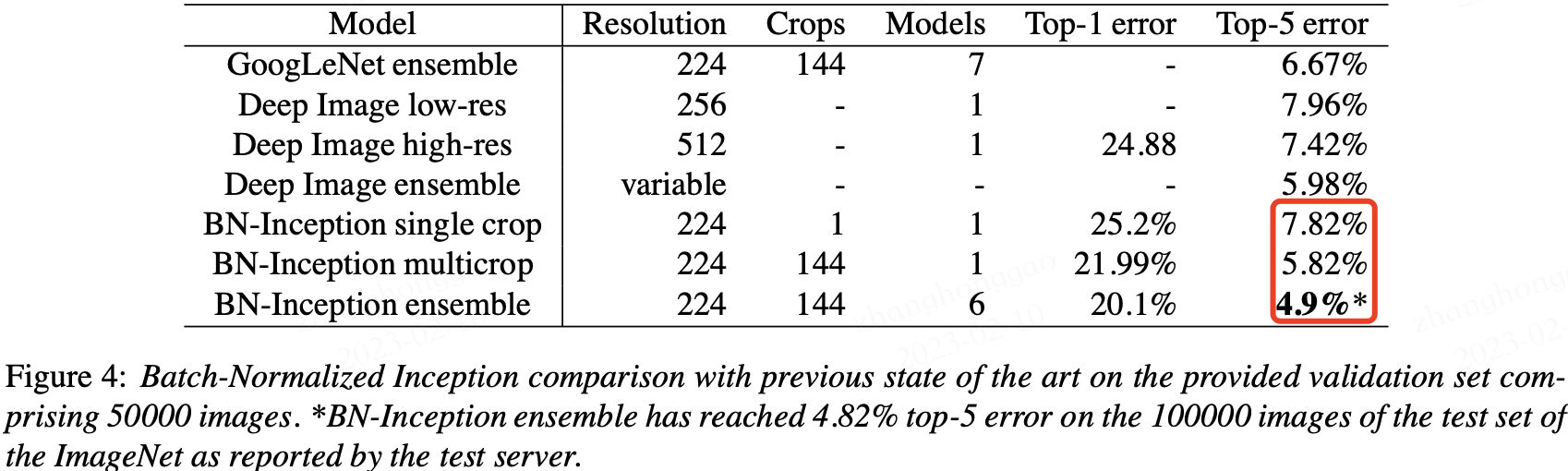






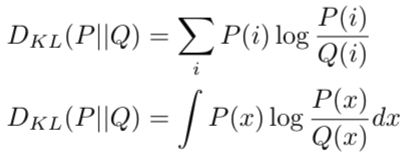

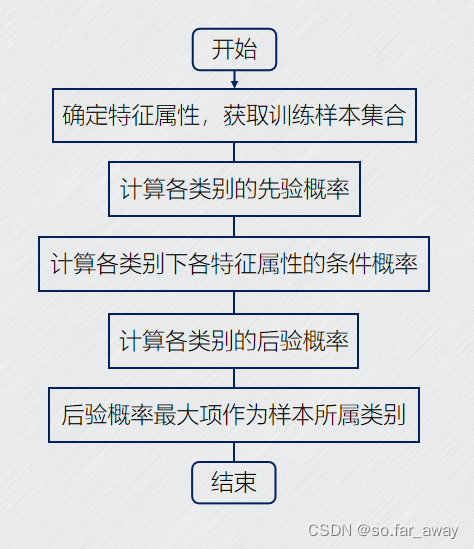


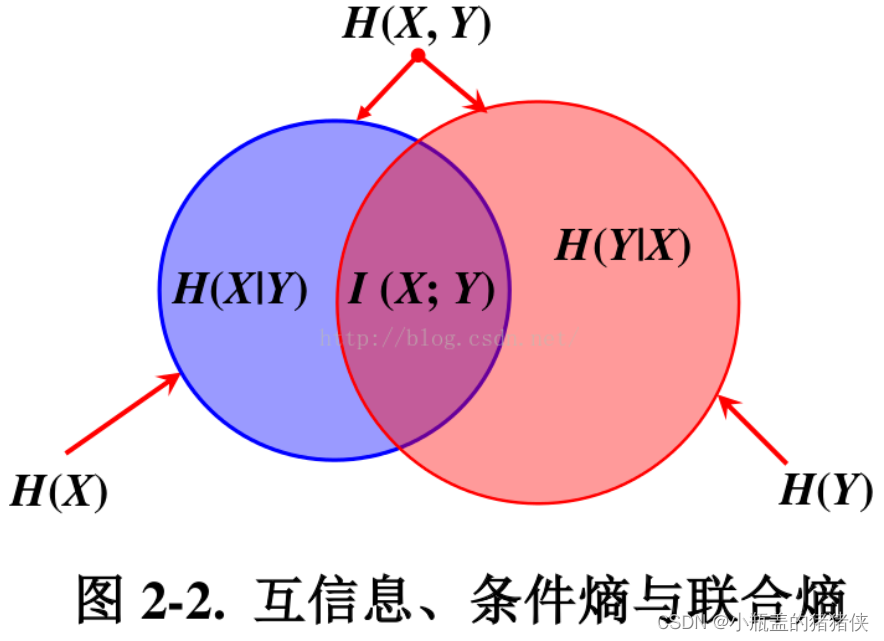
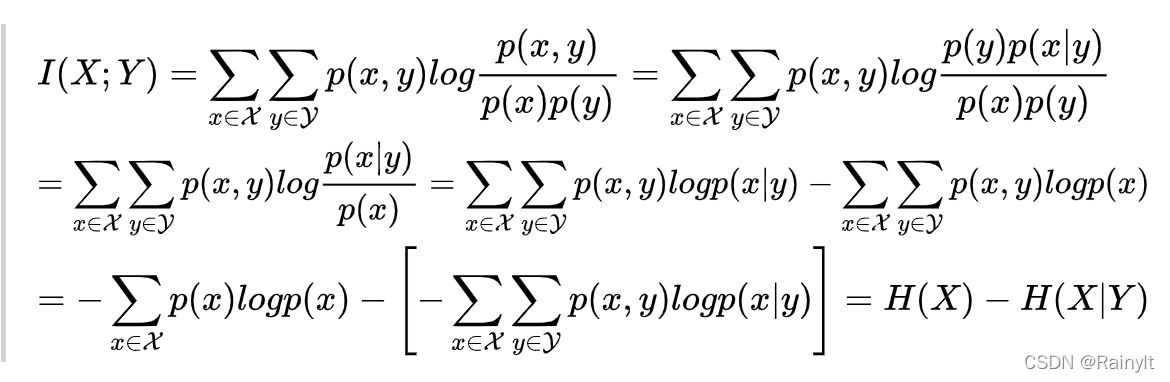
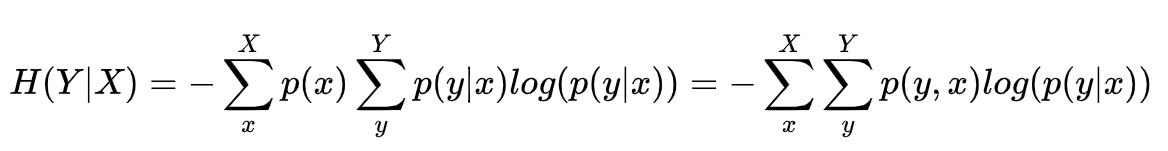


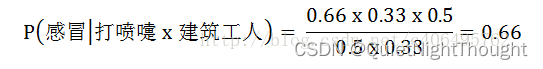




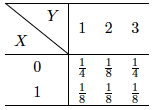









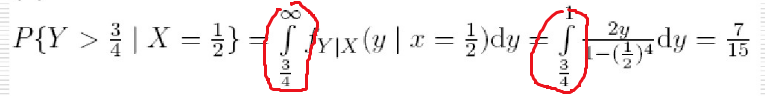


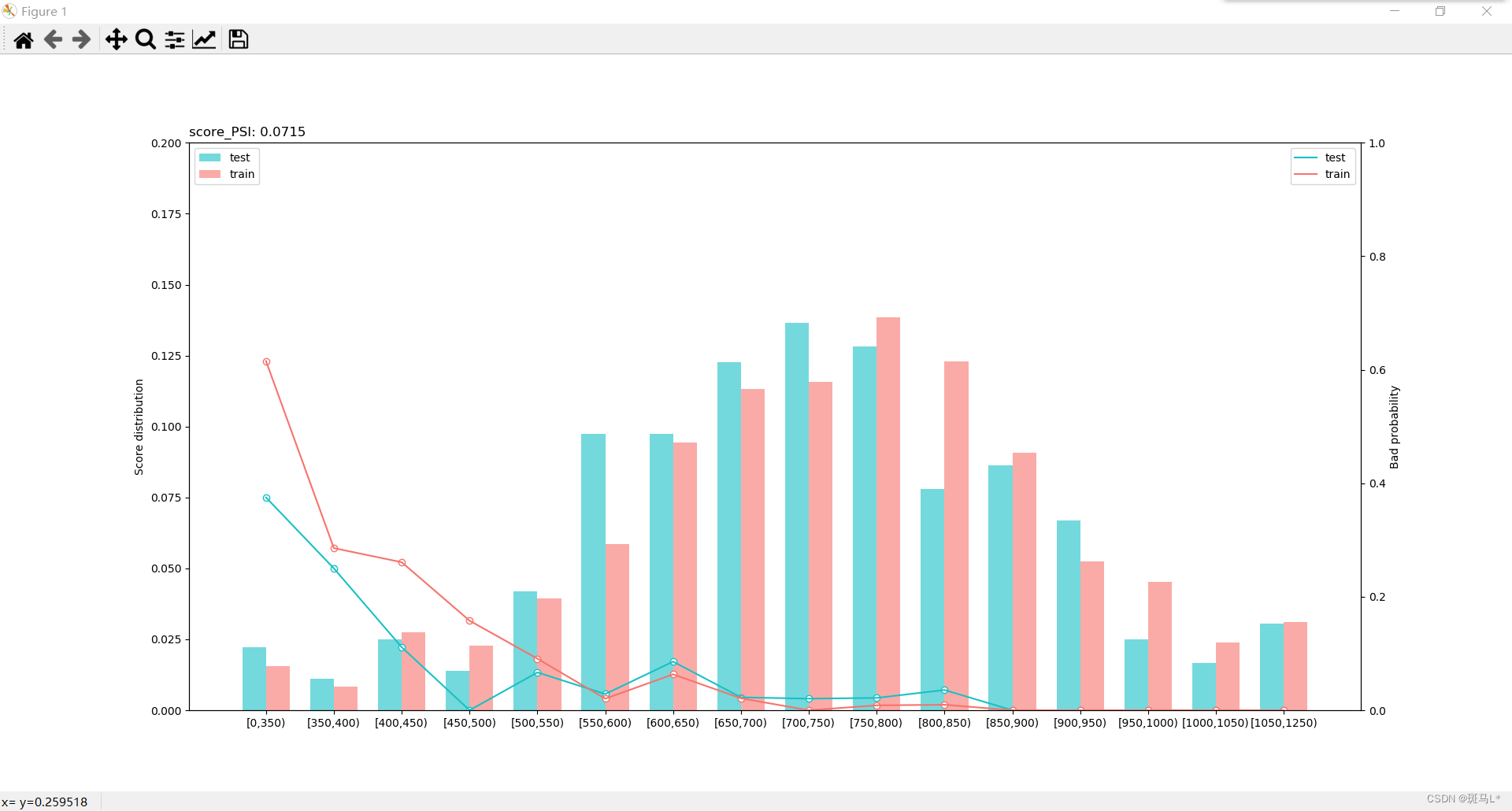














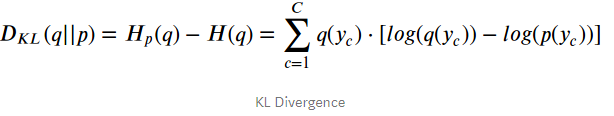













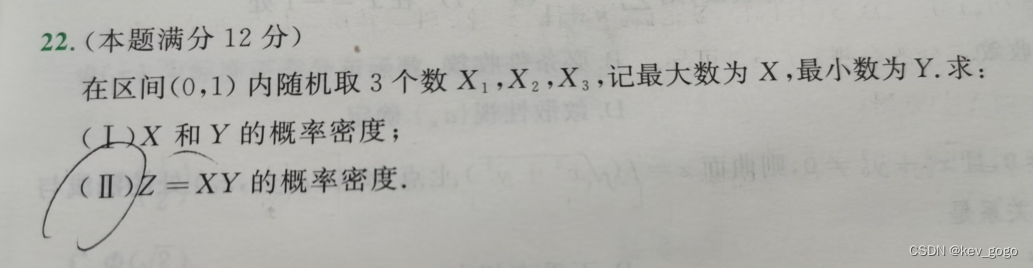





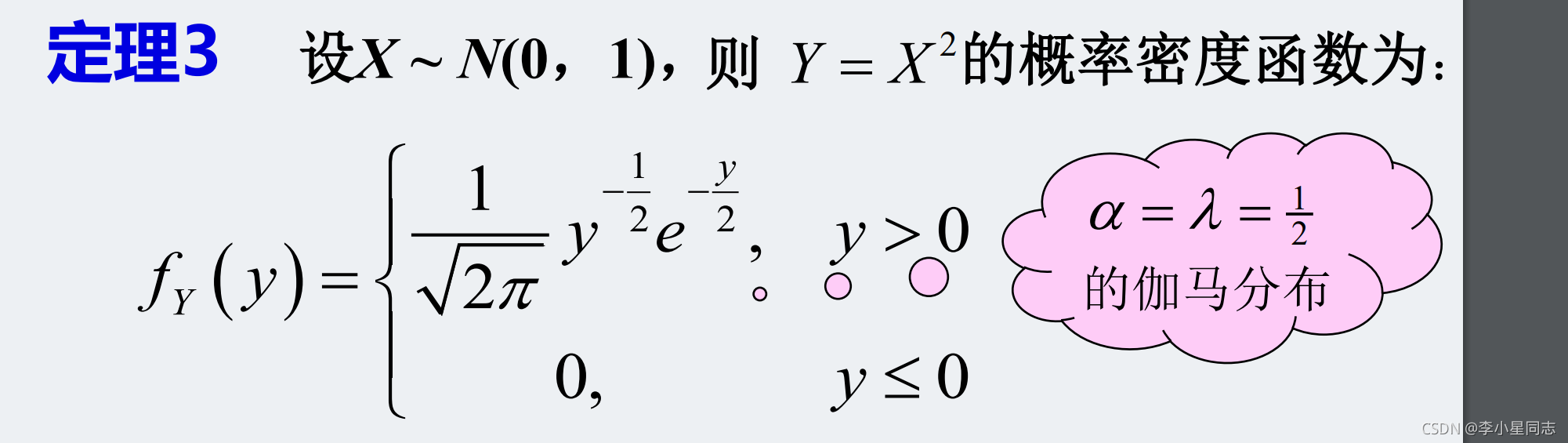










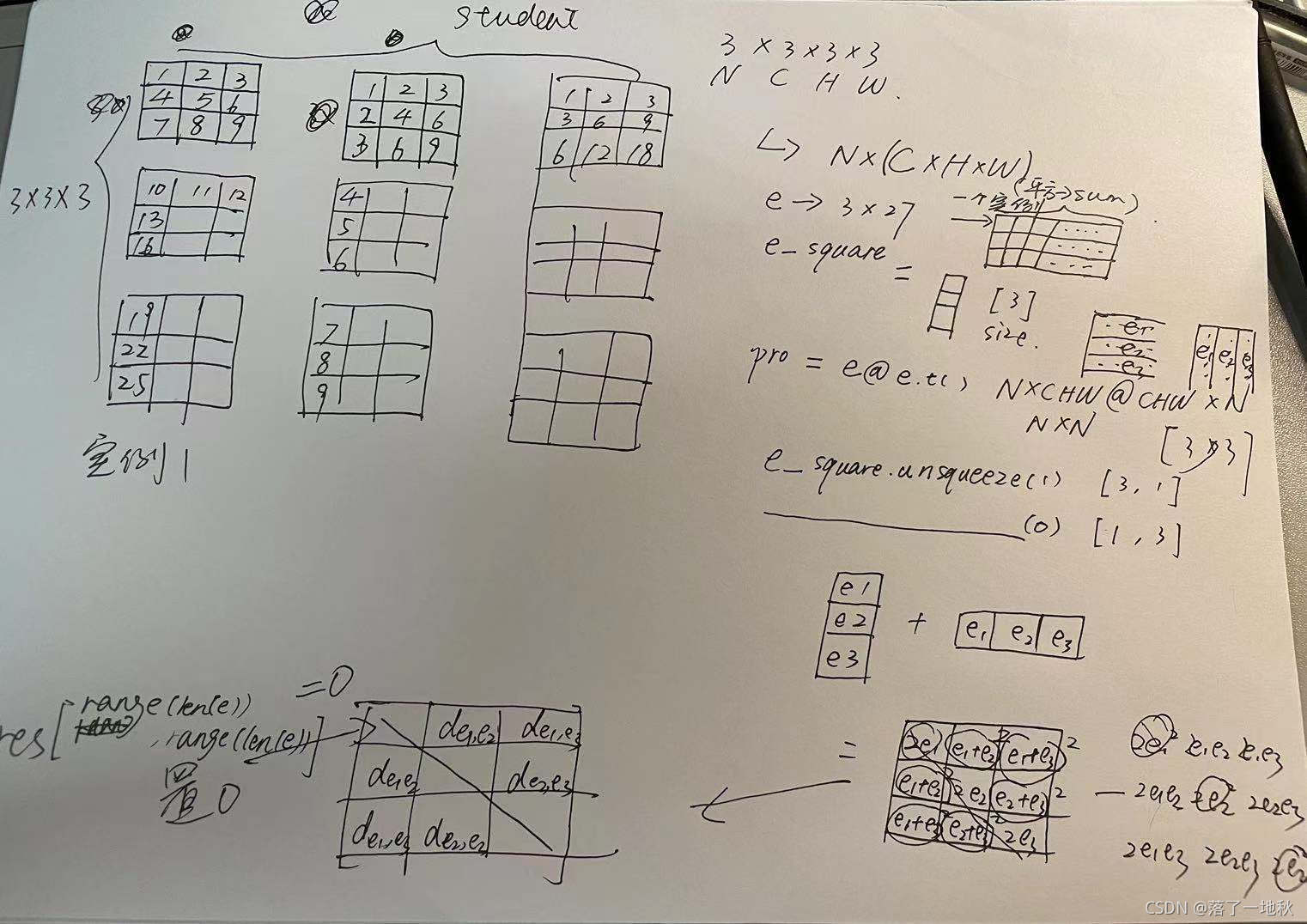
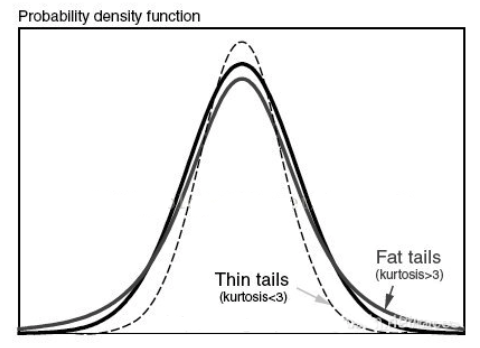



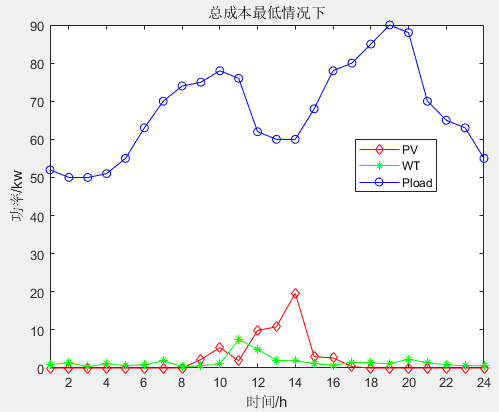

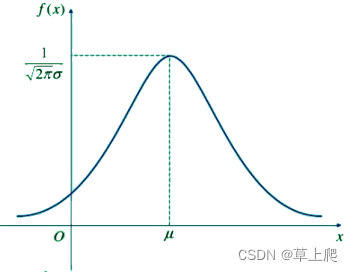



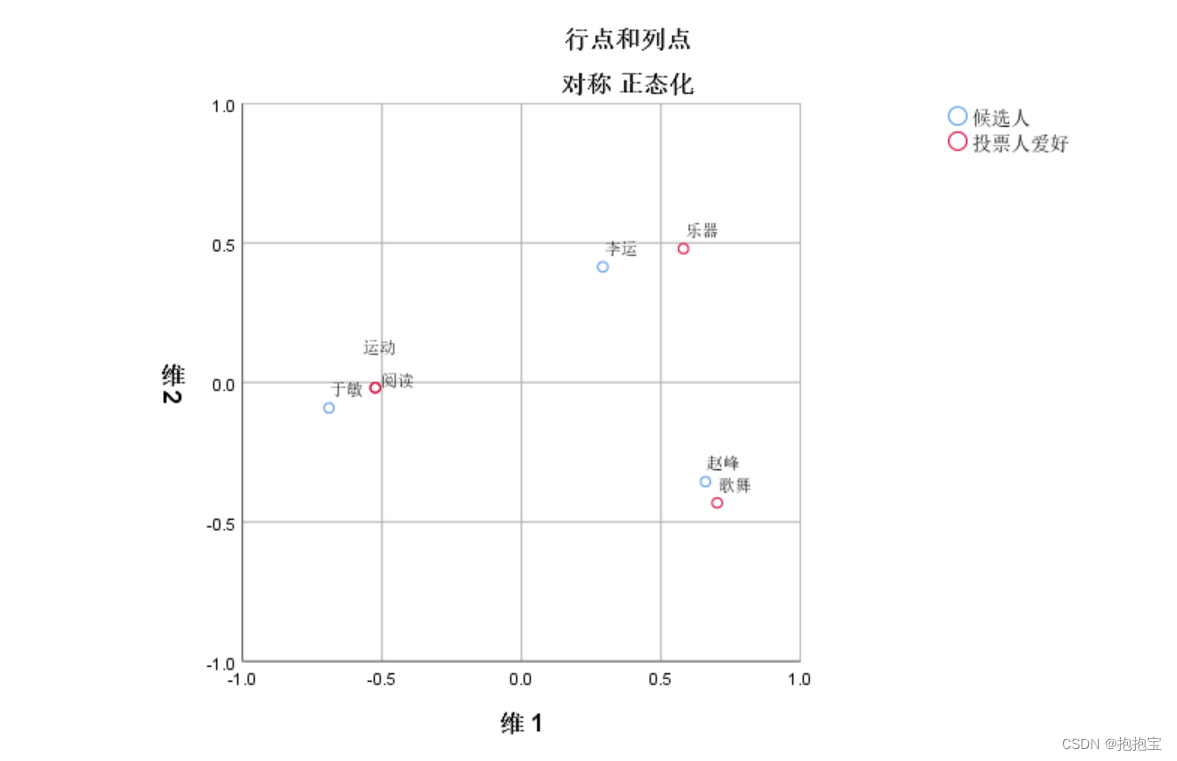

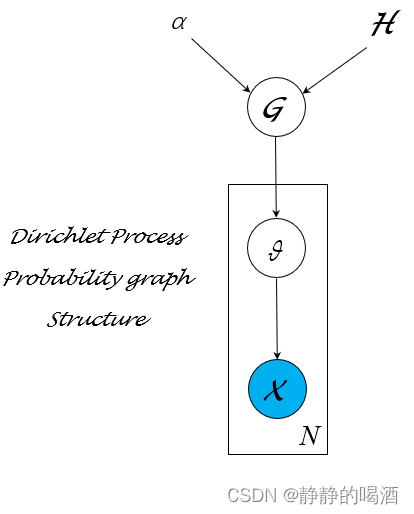


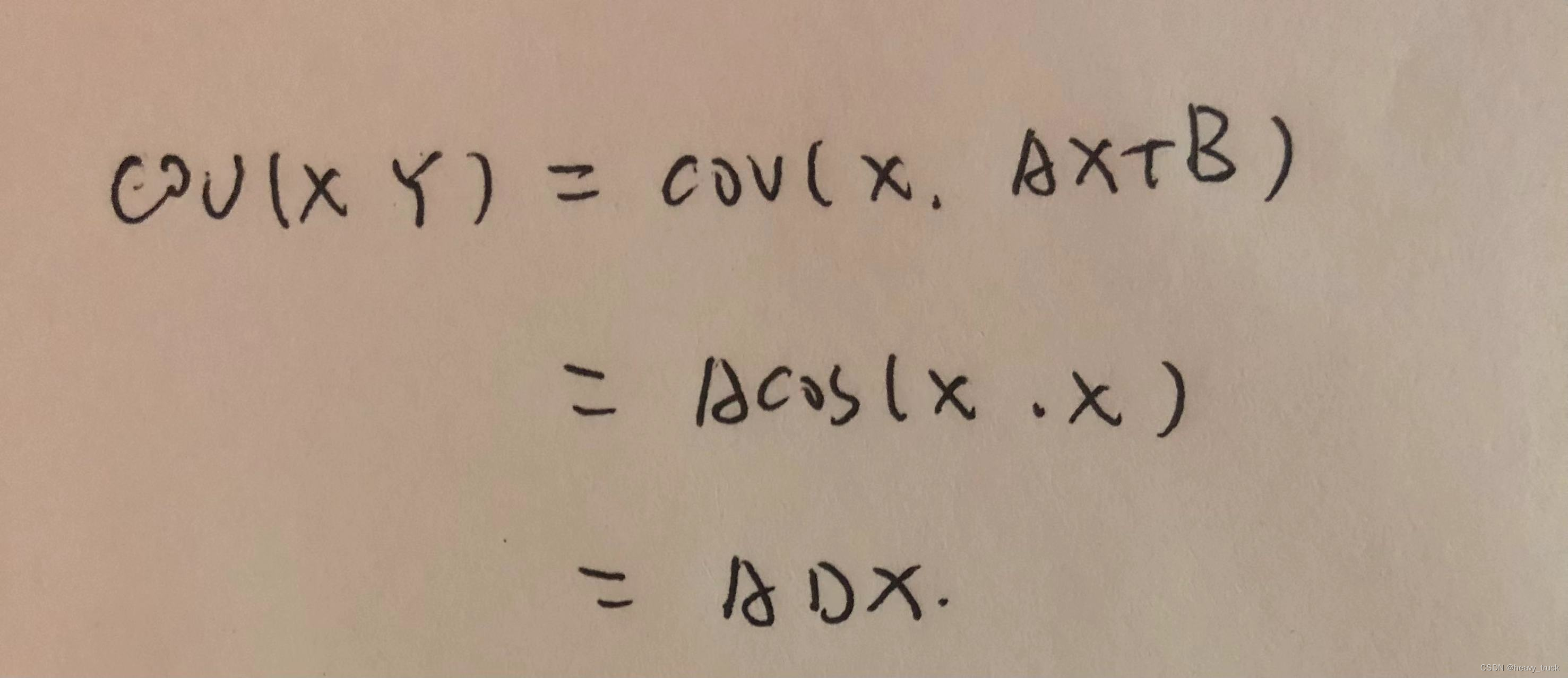




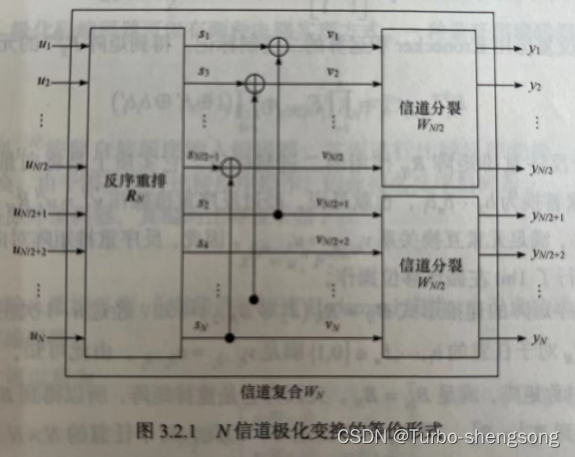

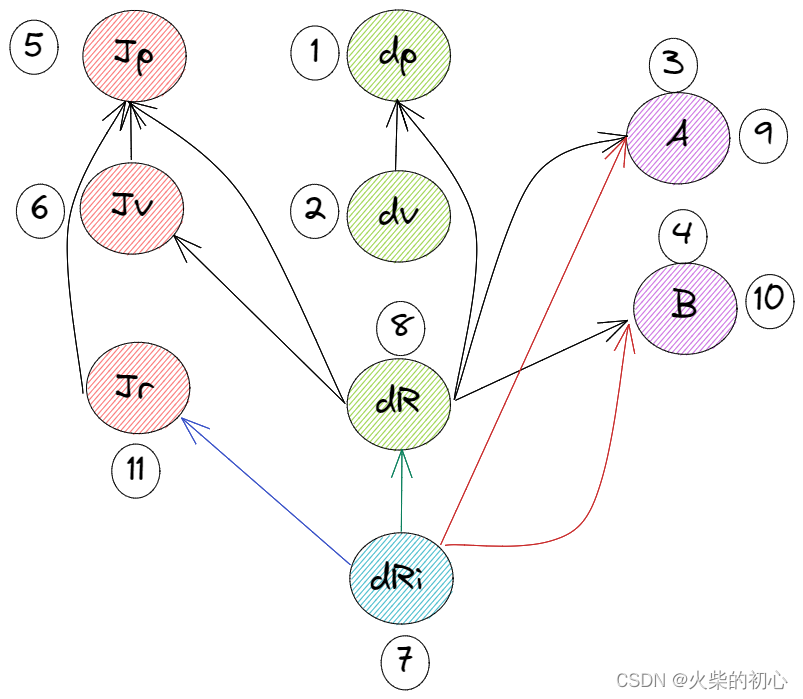


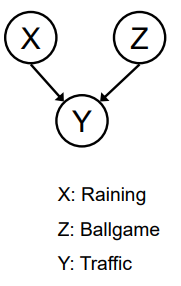
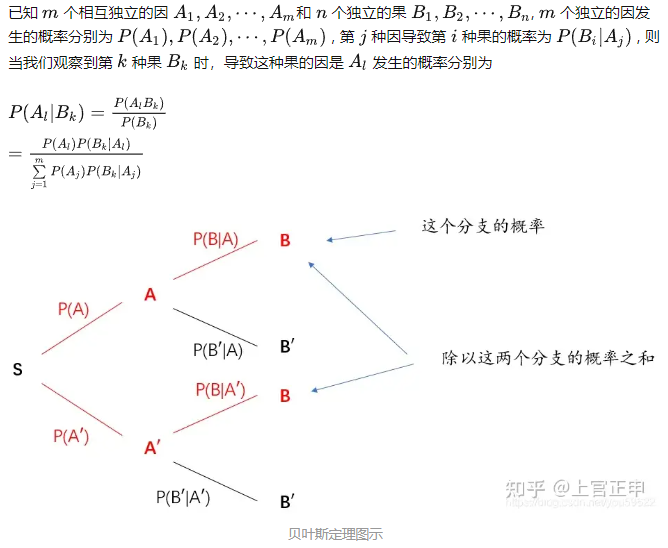




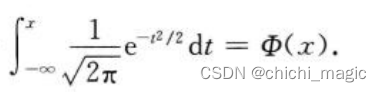
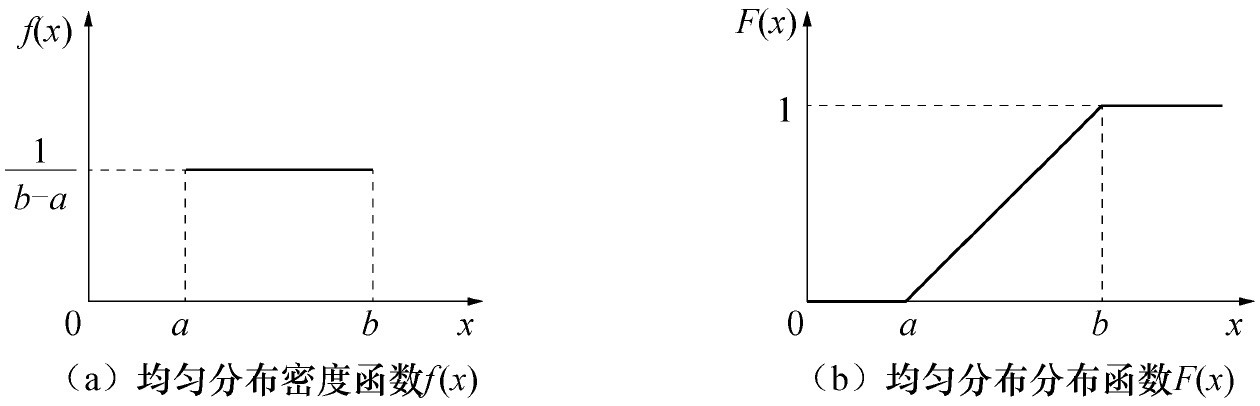


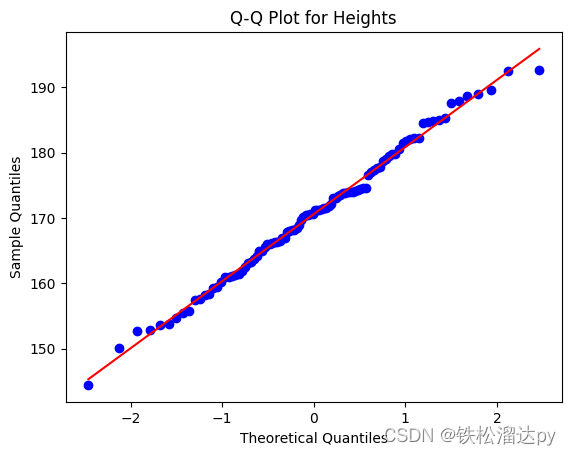
![@[计算方法]蒙特卡罗投点](https://img-blog.csdnimg.cn/20200420090859562.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM4NzUxNQ==,size_16,color_FFFFFF,t_70#pic_center)


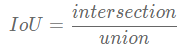
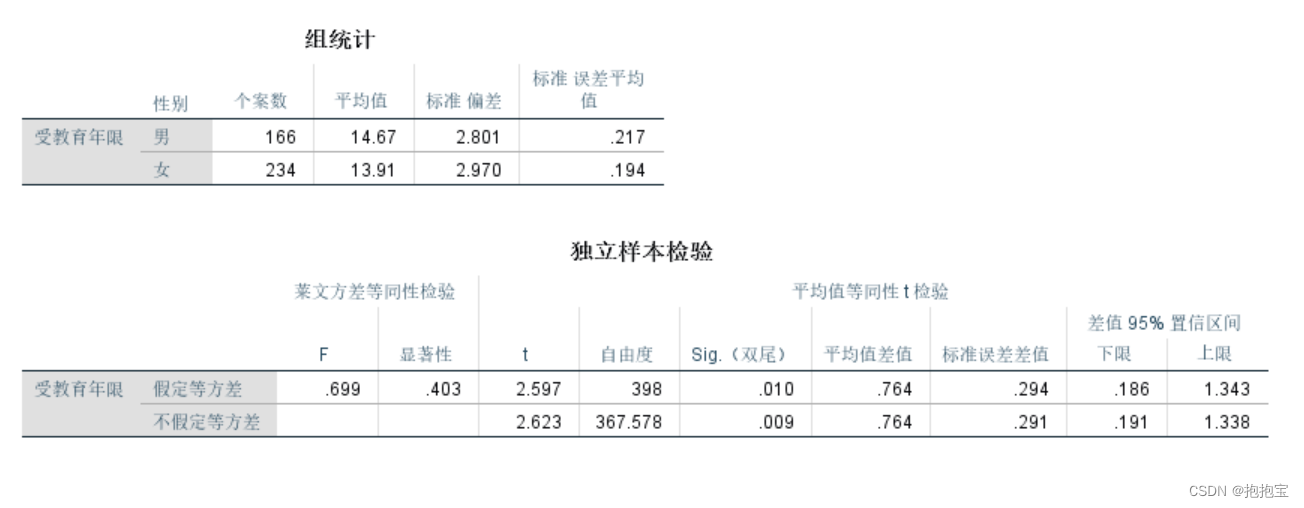

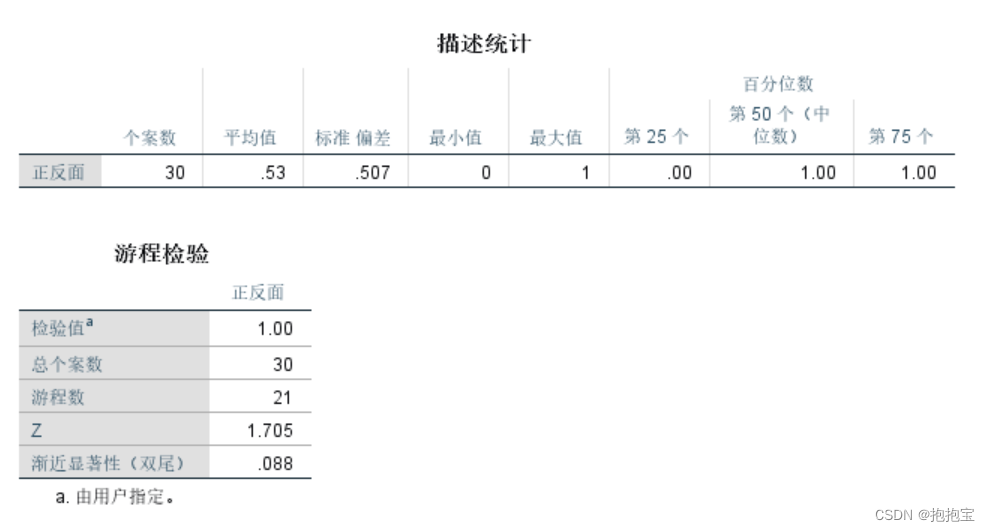

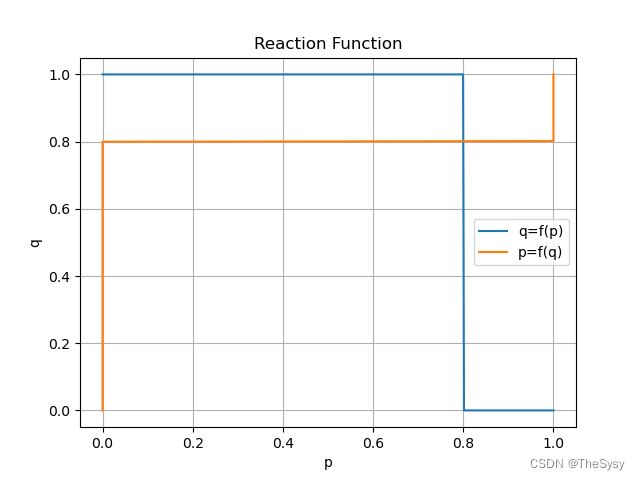

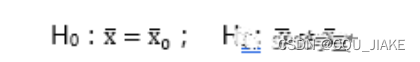





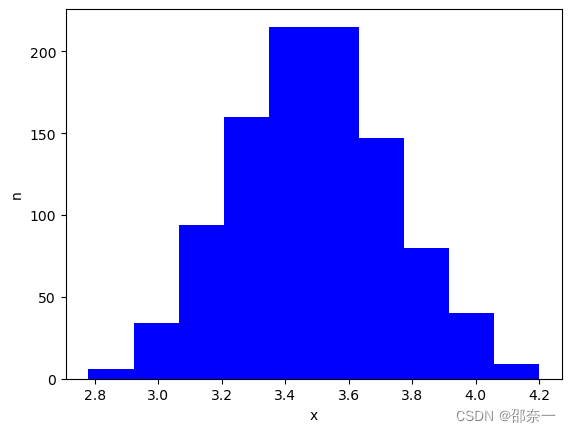
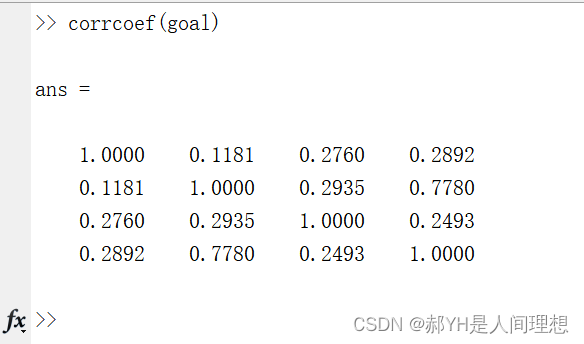


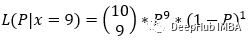
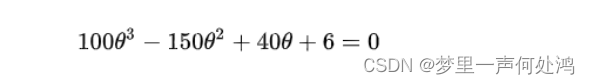


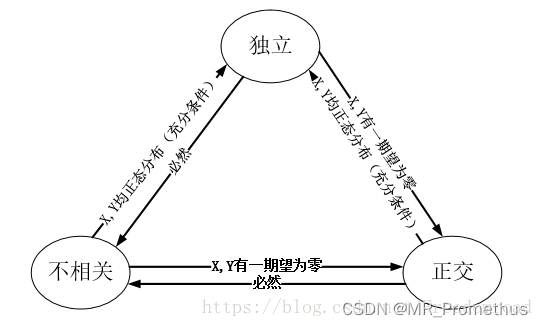




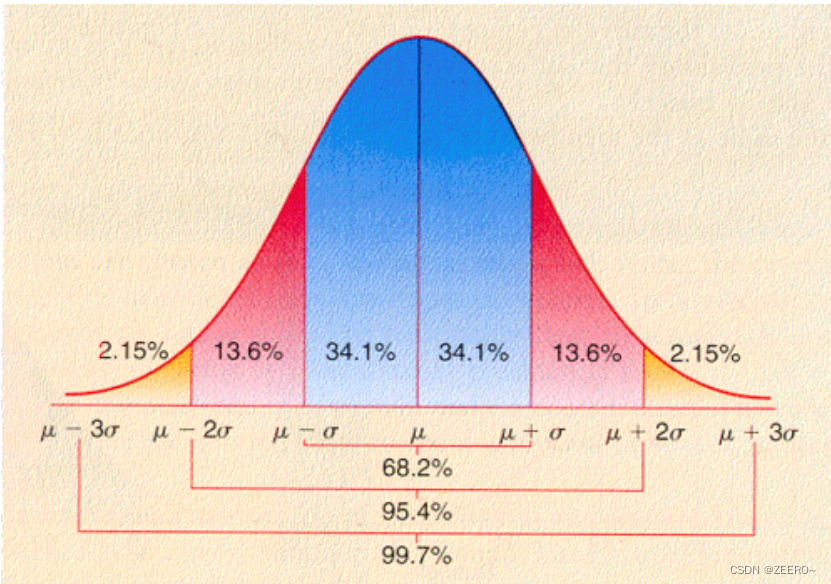

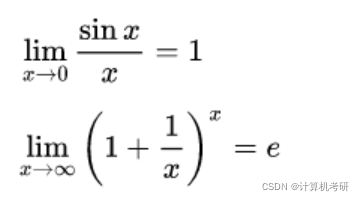



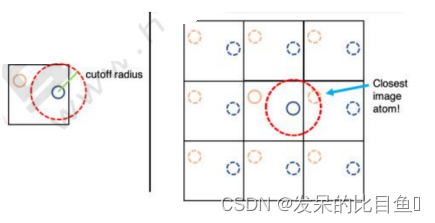


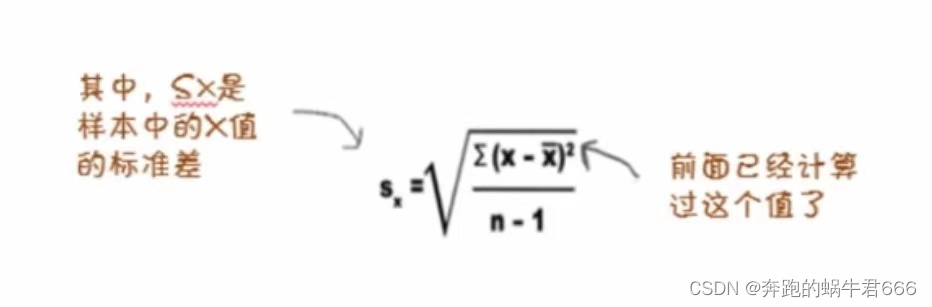


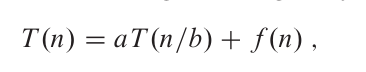


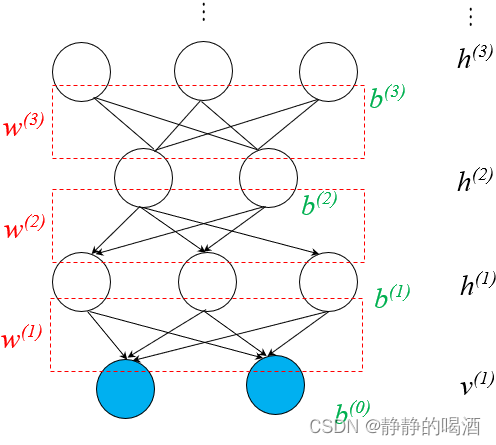


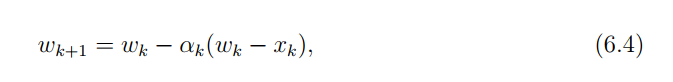

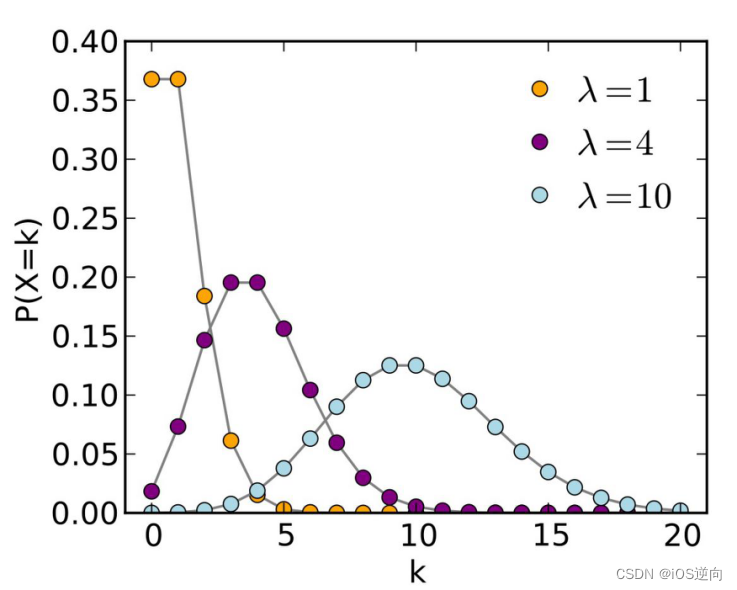

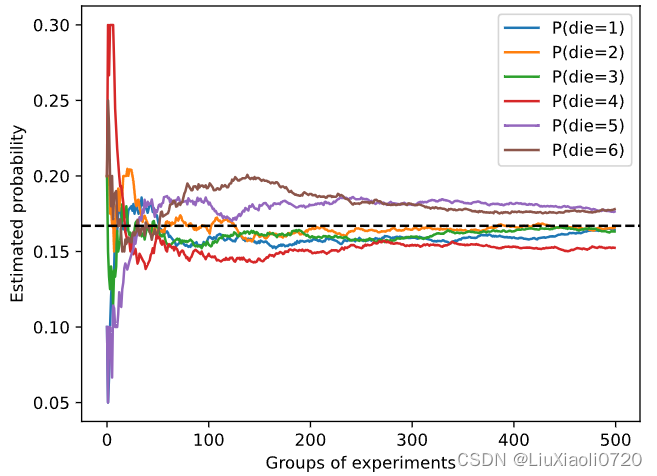



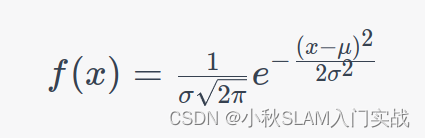
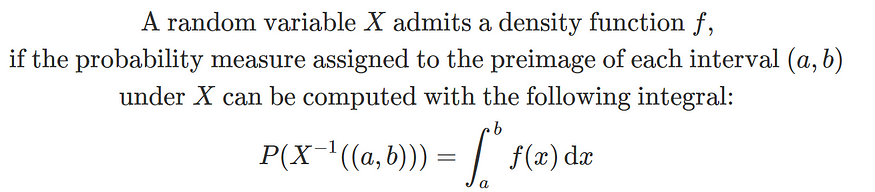

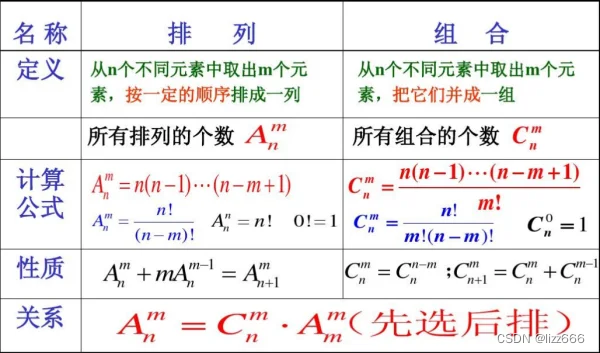


![概率中的50个具有挑战性的问题[03/50]:轻率的陪审员](https://img-blog.csdnimg.cn/img_convert/63fdf15be69b835c5e7e30645a986f67.png)
![概率中的50个具有挑战性的问题[02/50]:连续获胜](https://img-blog.csdnimg.cn/img_convert/fab2aae23fd92fec5d5018ff37b32af2.png)


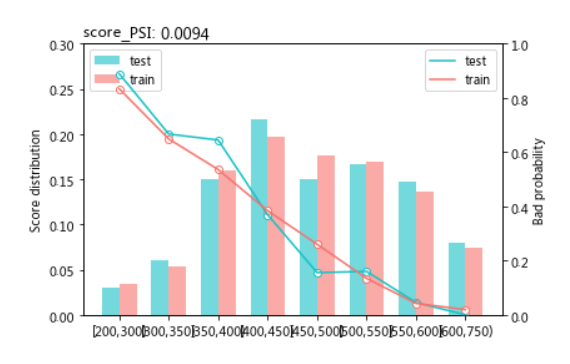
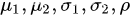


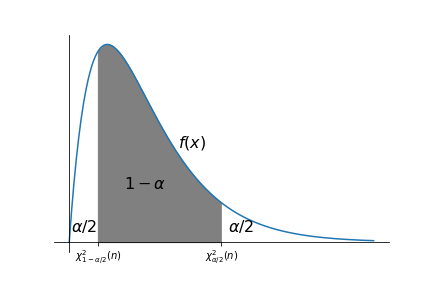

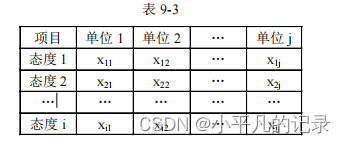




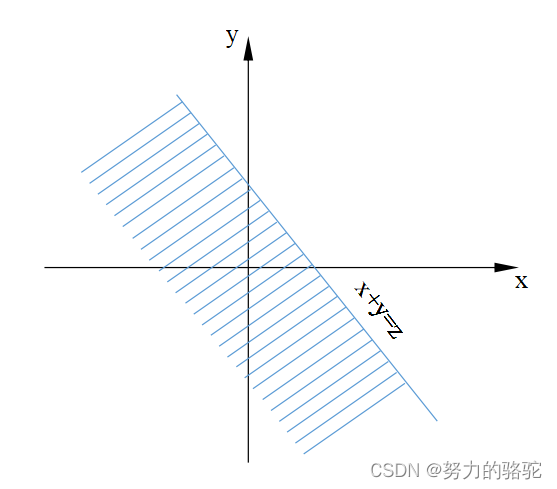

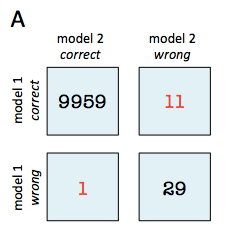
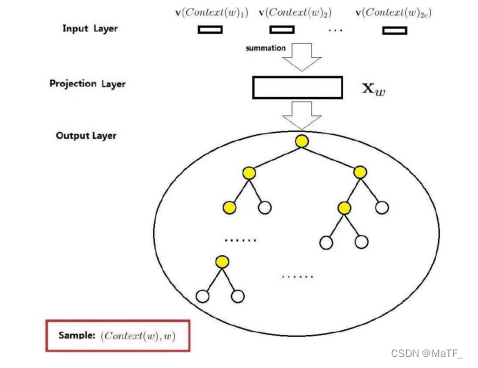
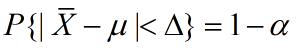




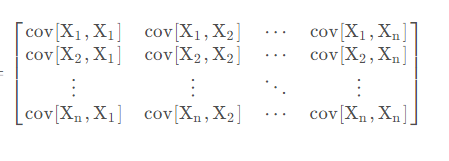


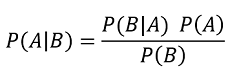

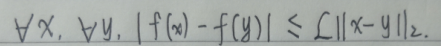

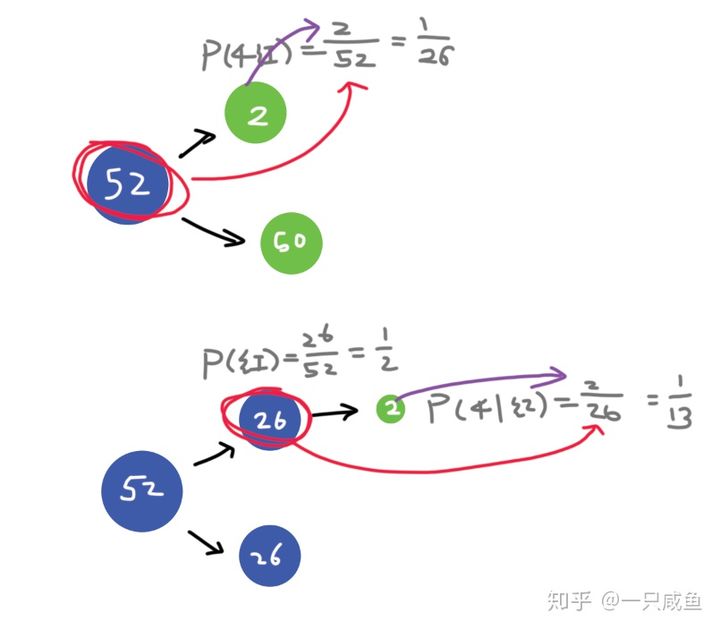
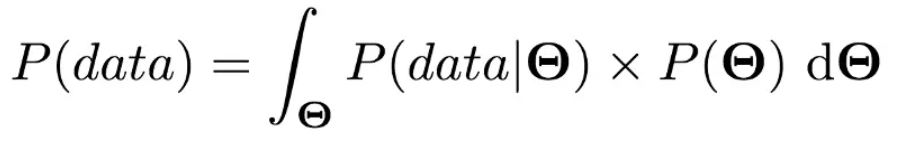


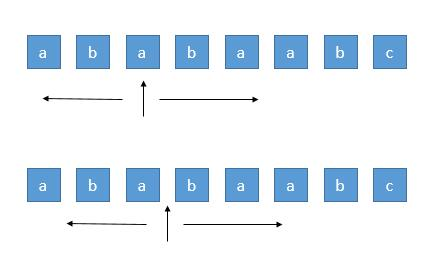



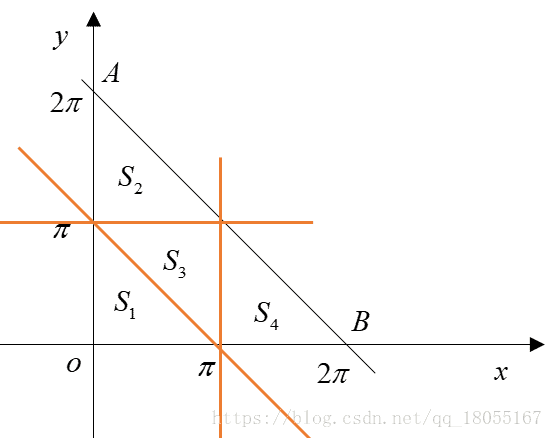









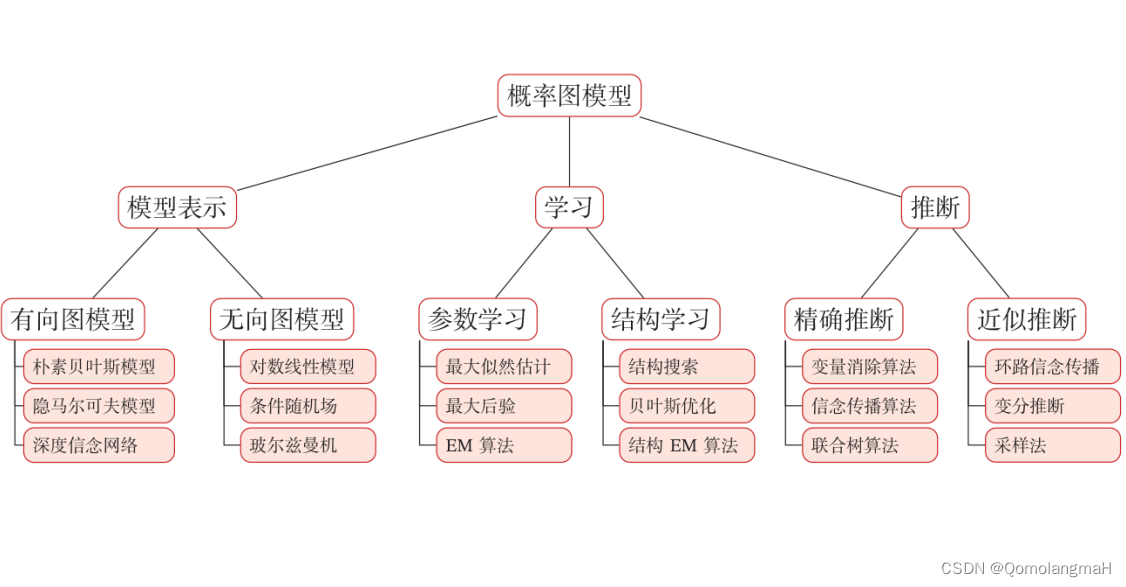

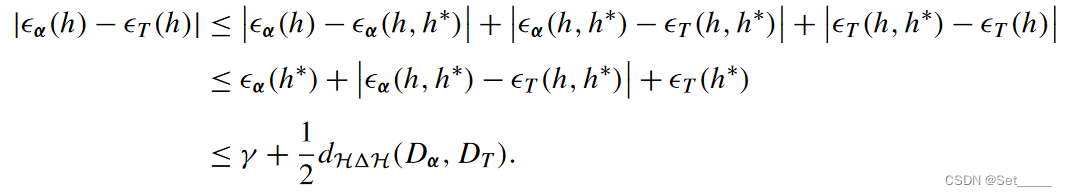
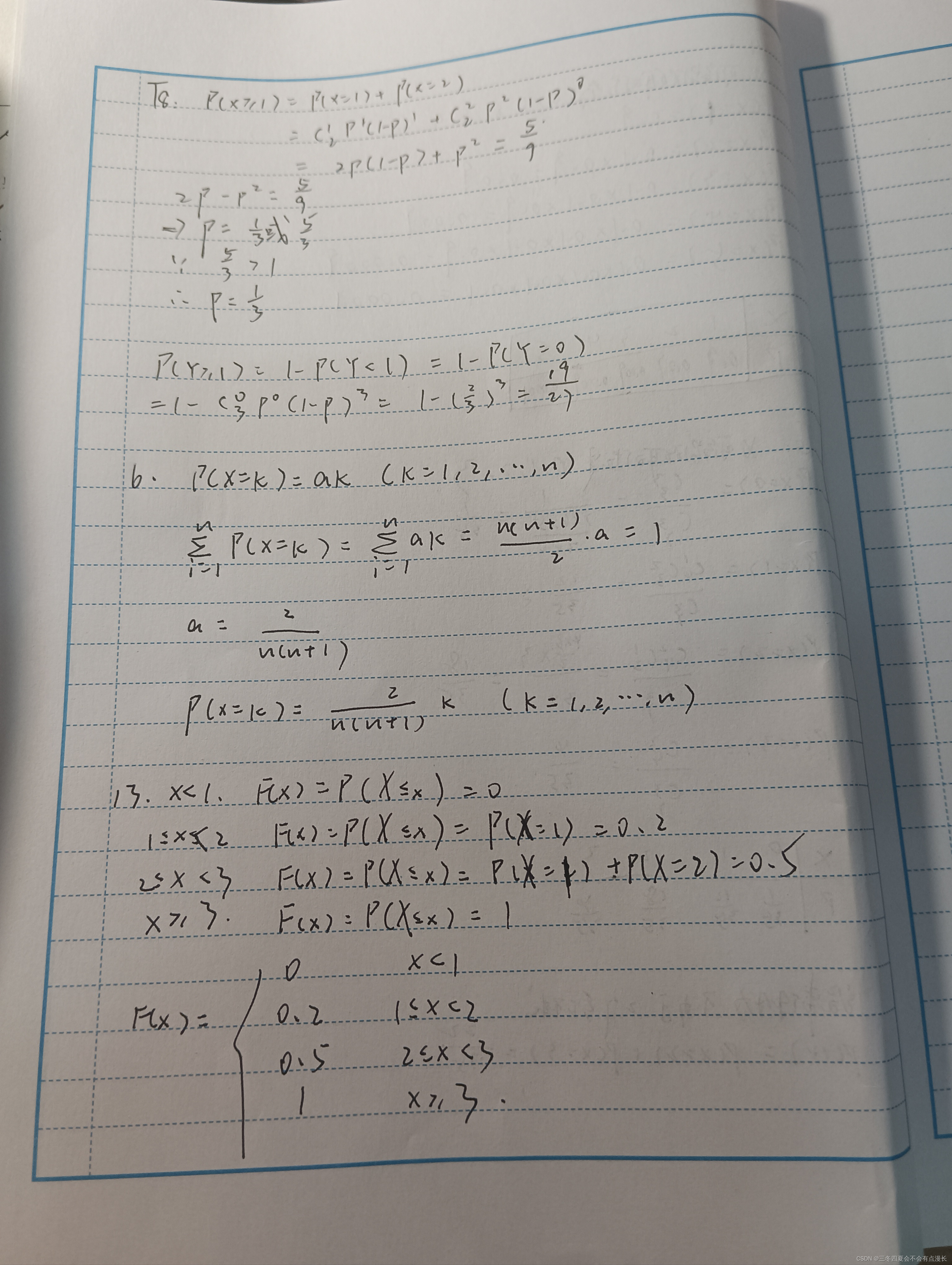
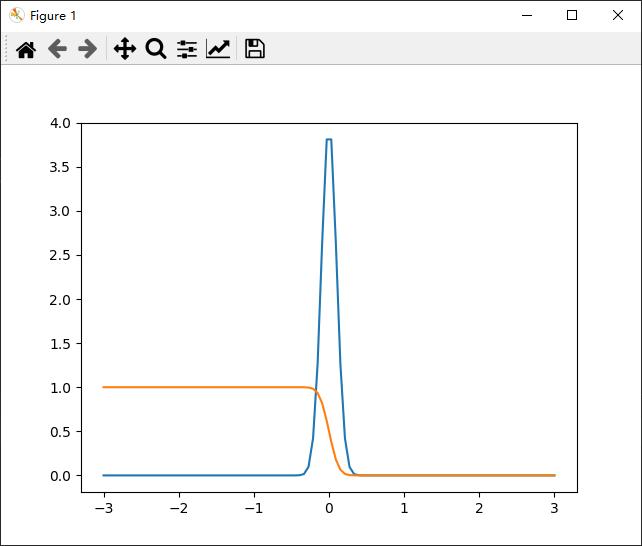
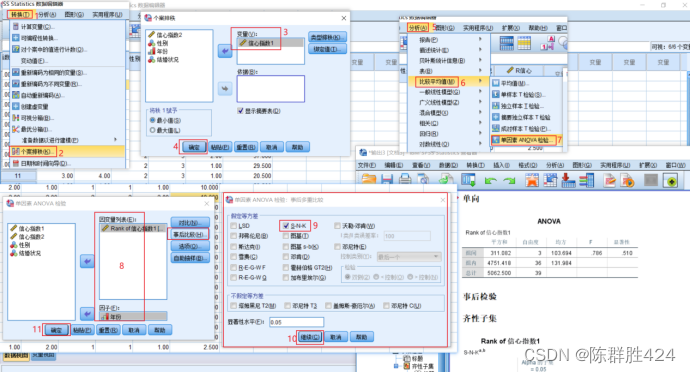

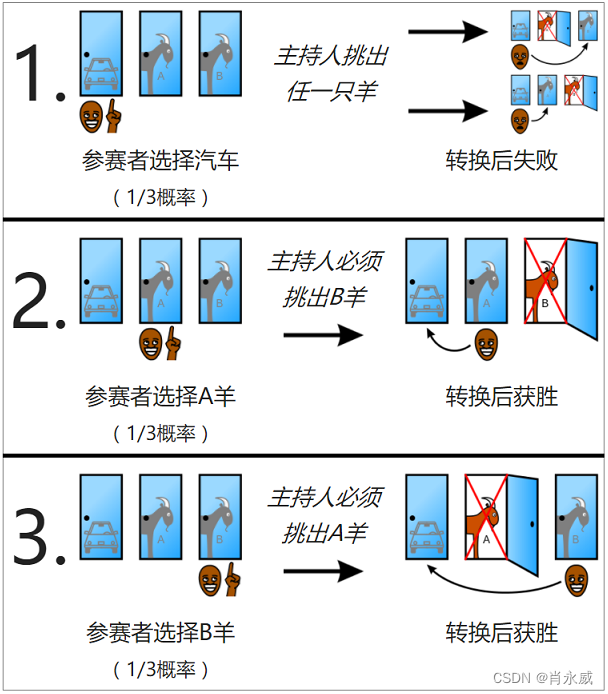


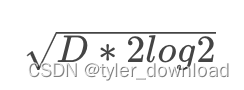

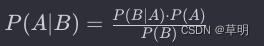
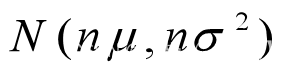
![概率中的 50 个具有挑战性的问题 [05/50]:正方形硬币](https://img-blog.csdnimg.cn/direct/396a3369e9db4e9e8d7d252b1f9dd252.png)



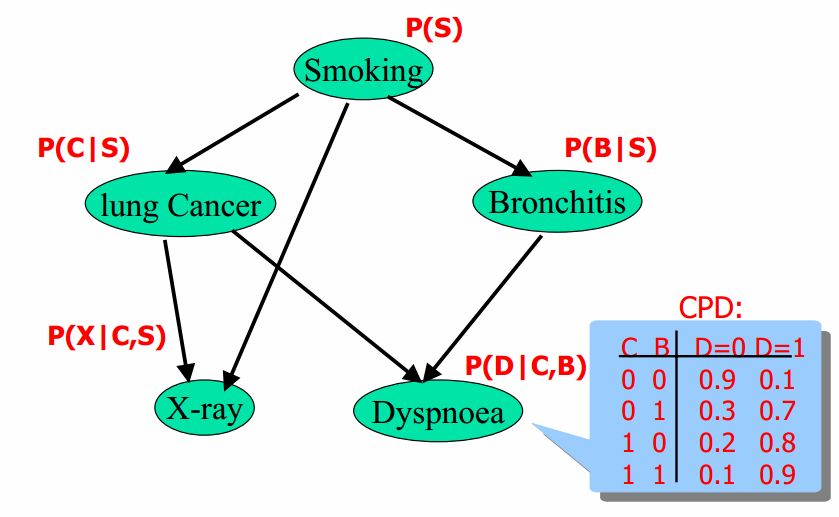



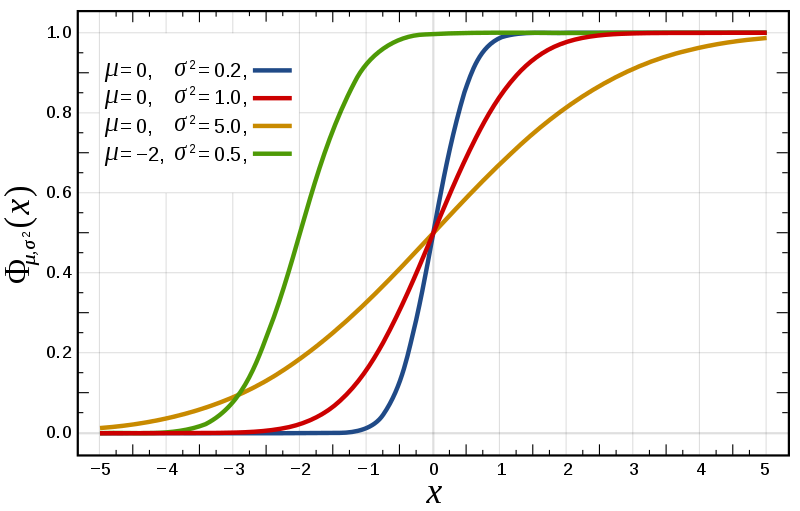




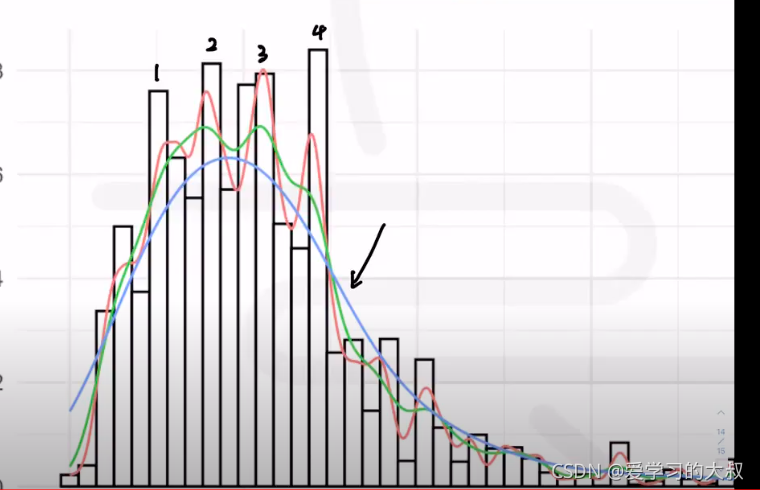
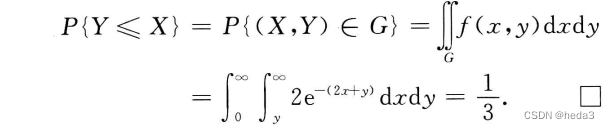

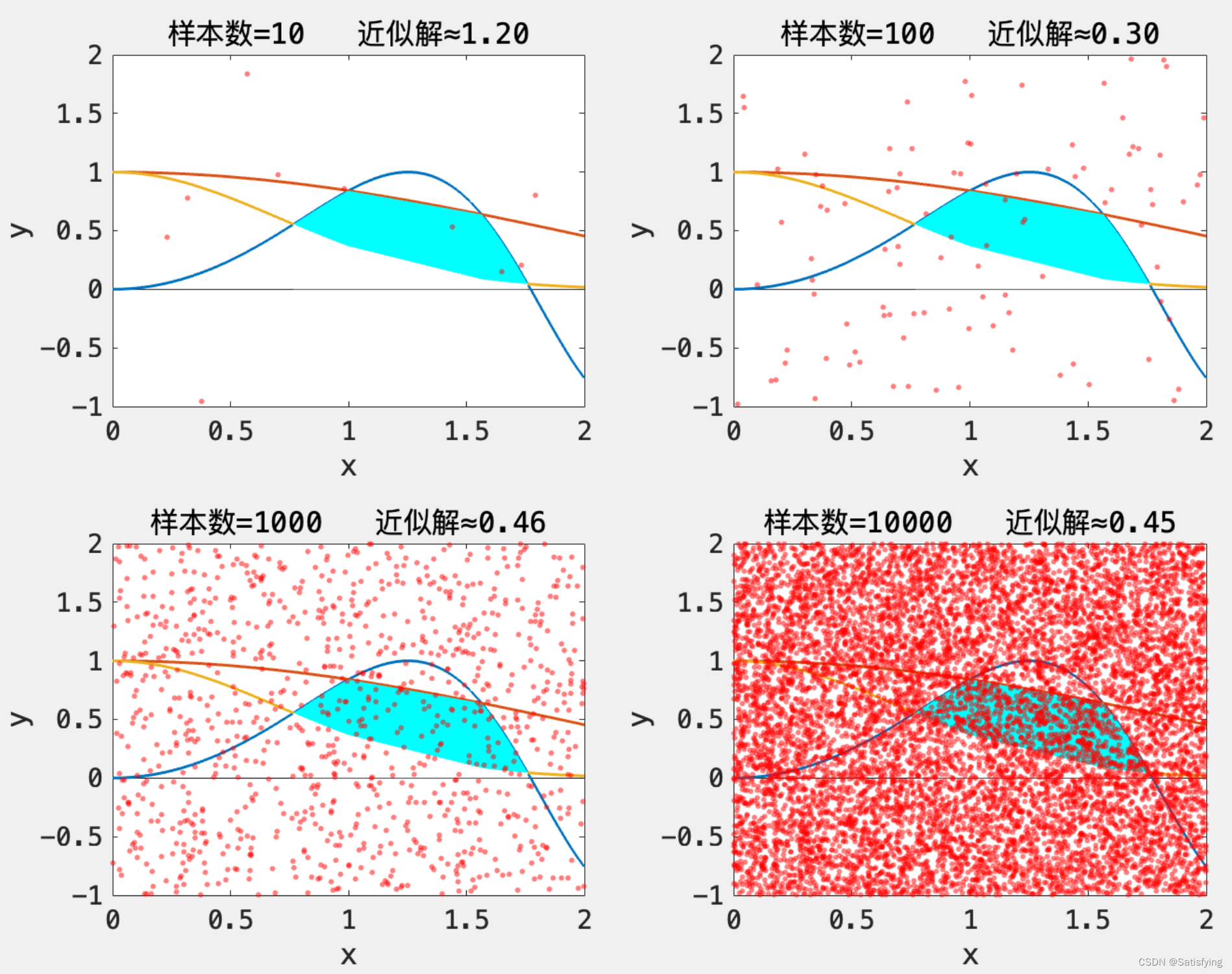






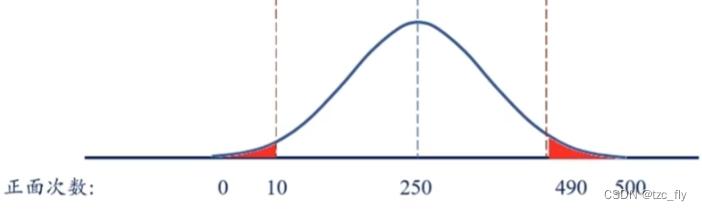
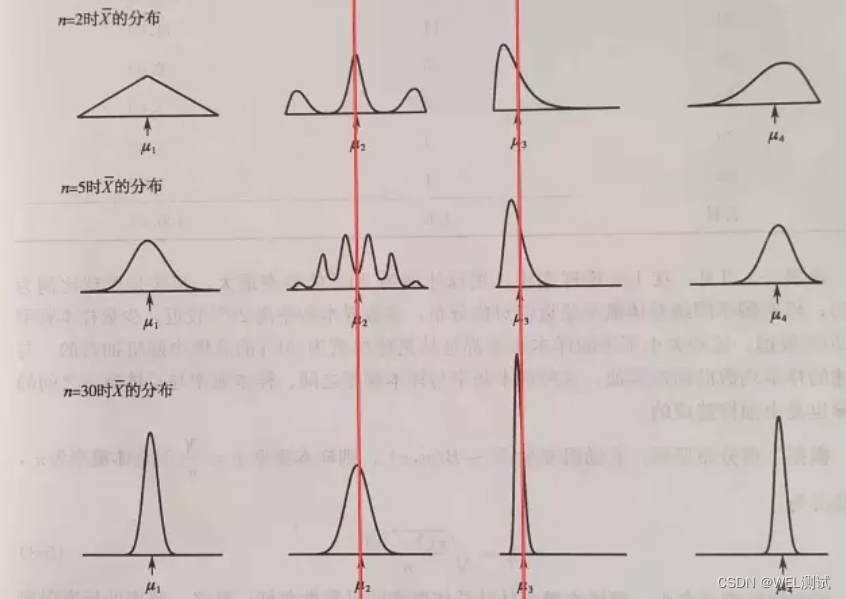



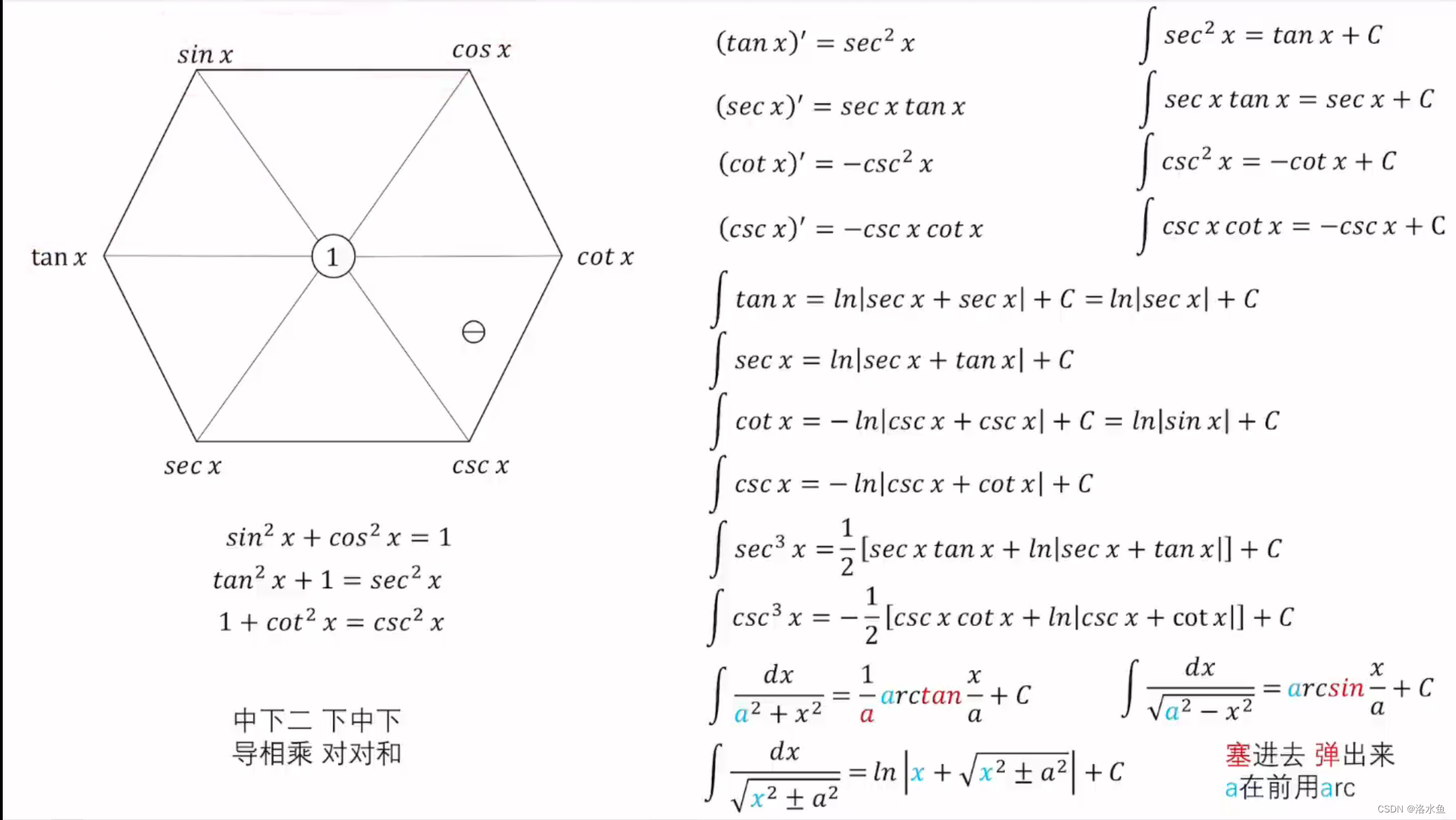
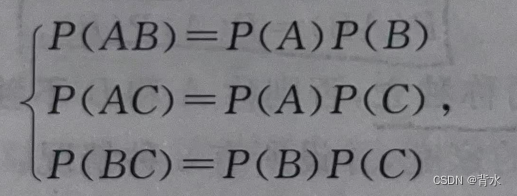

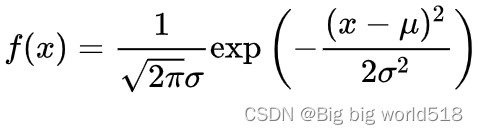
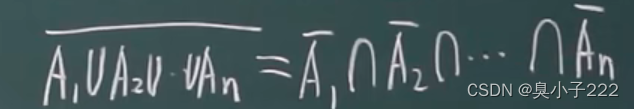







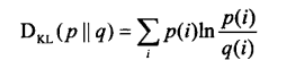






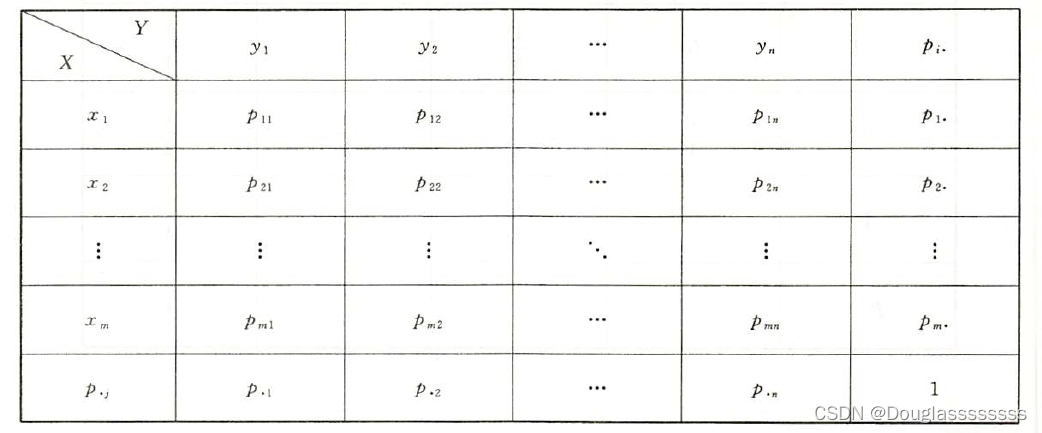
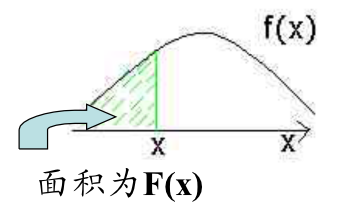
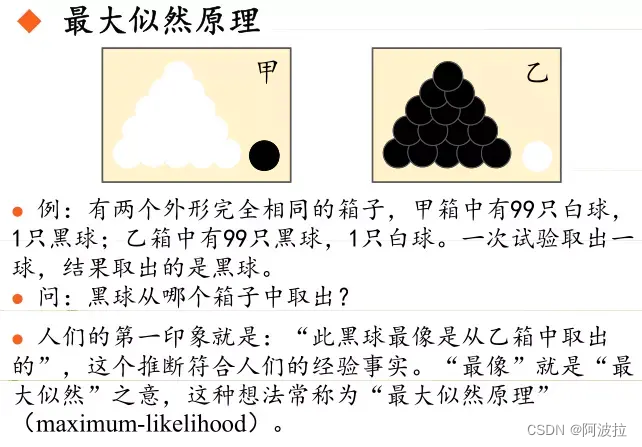

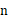

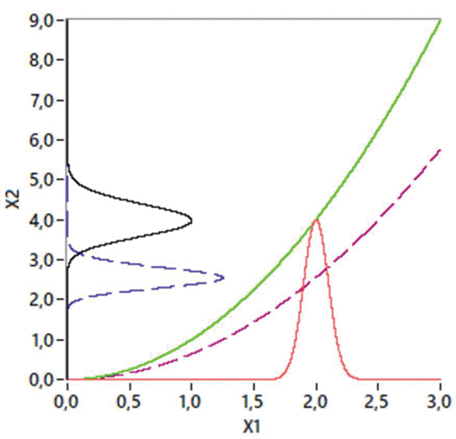








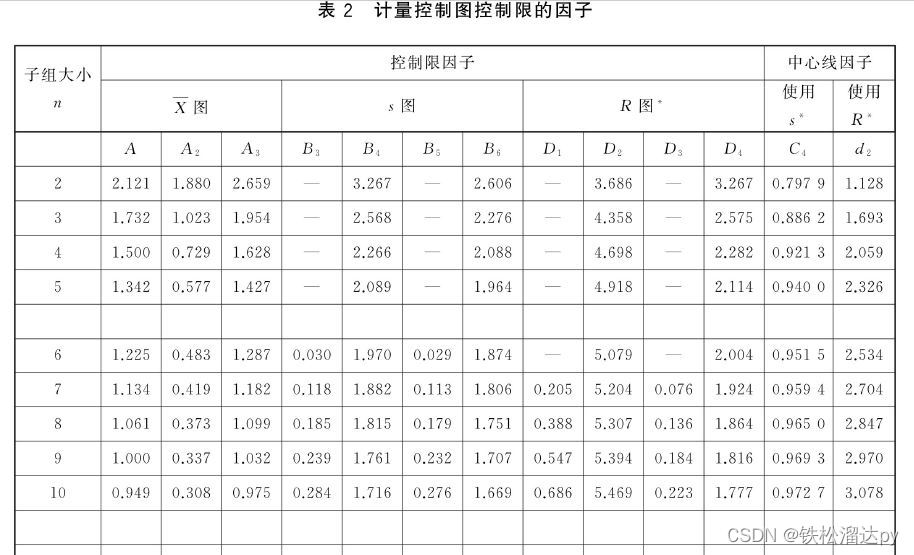




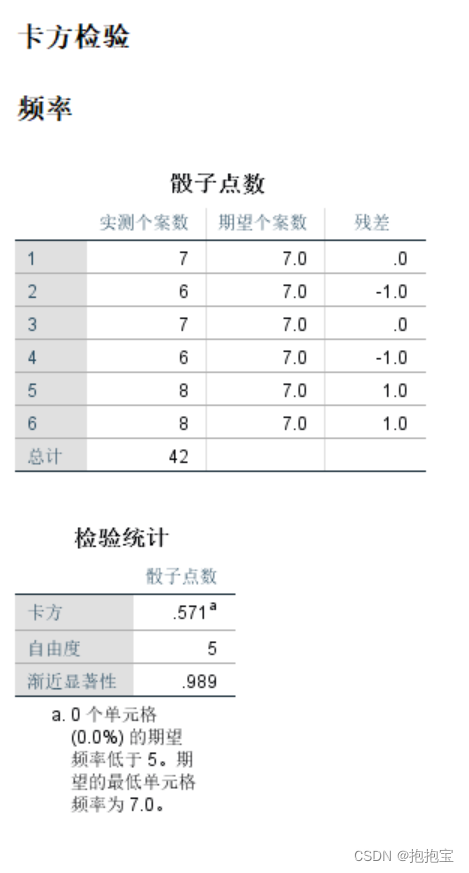
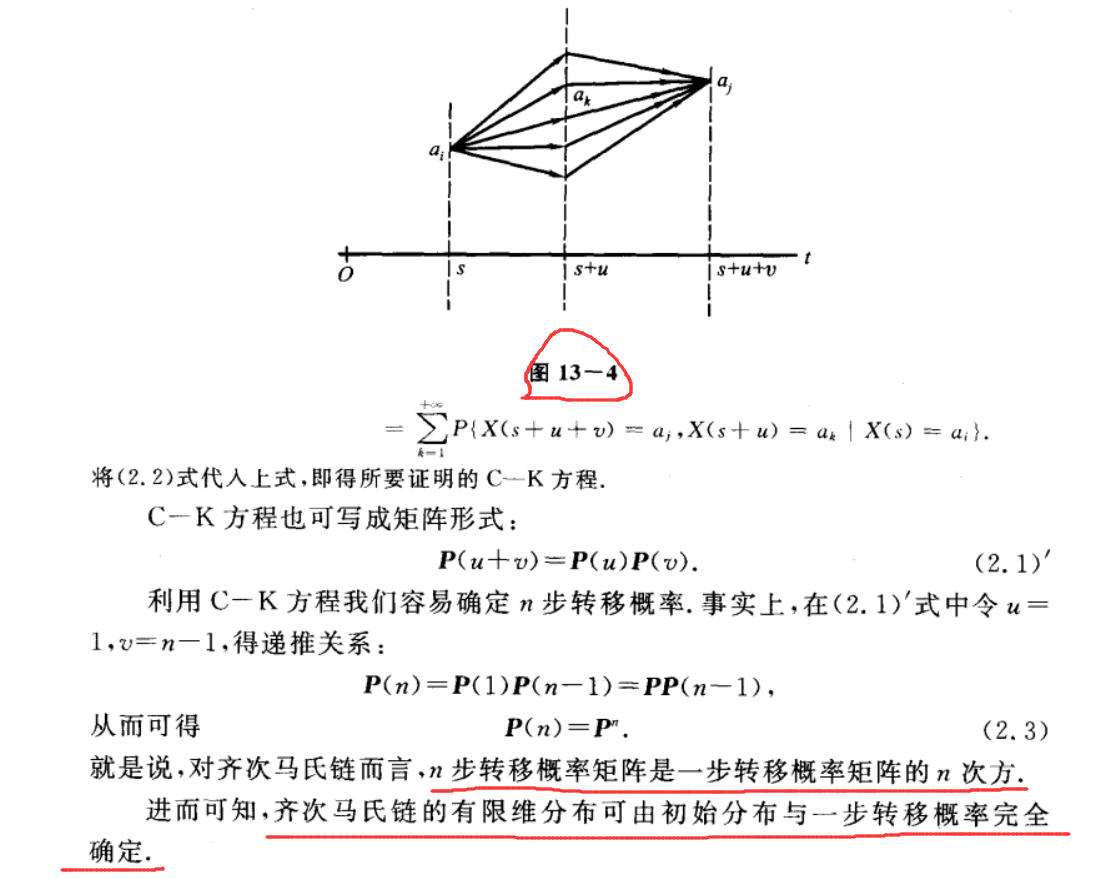


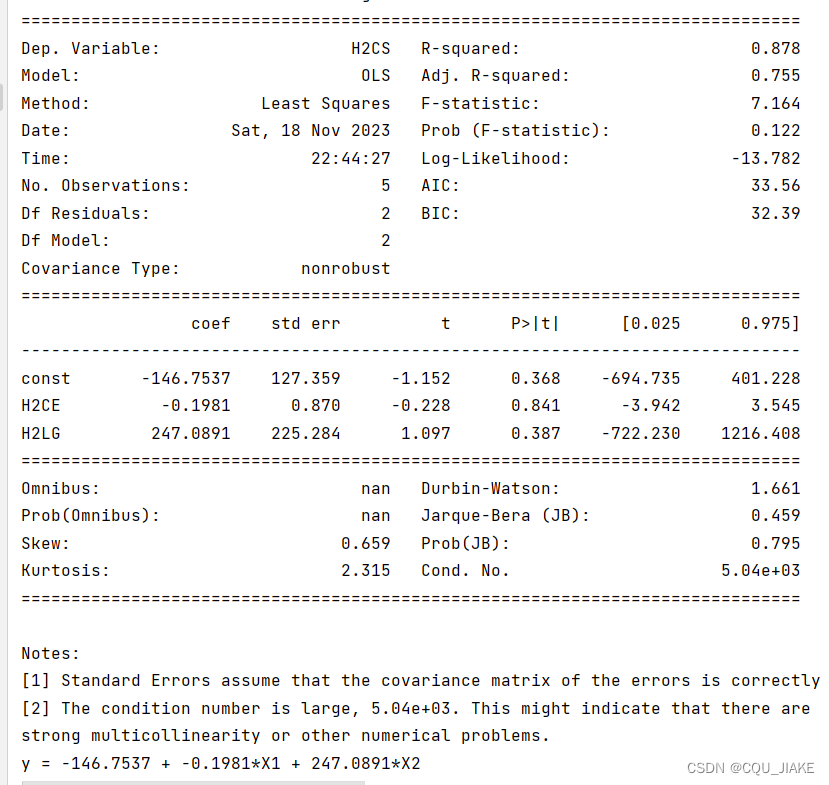
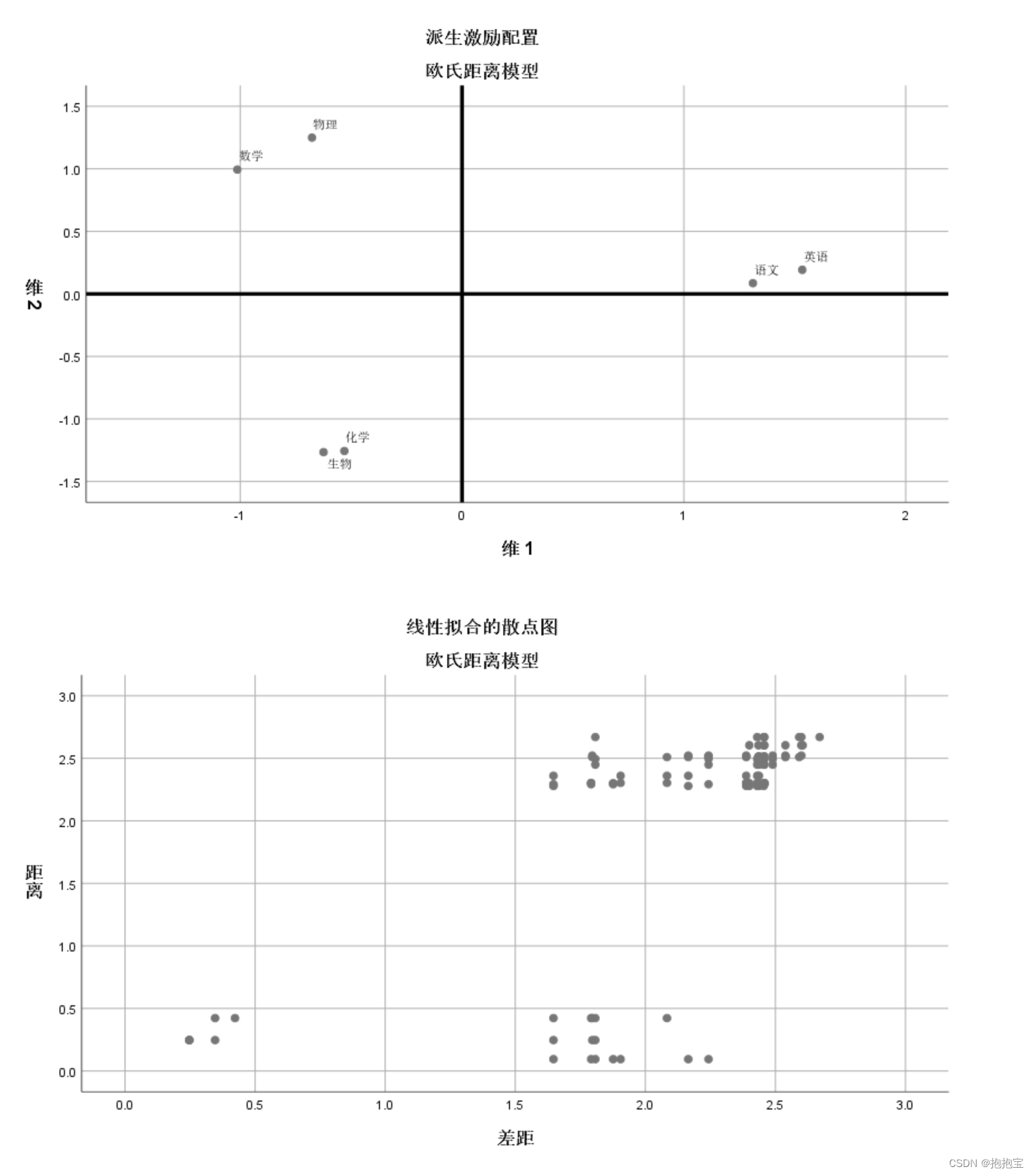
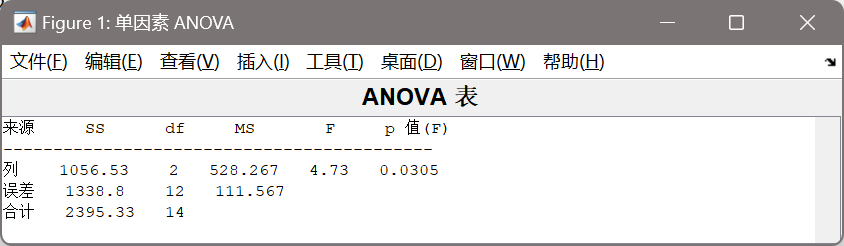


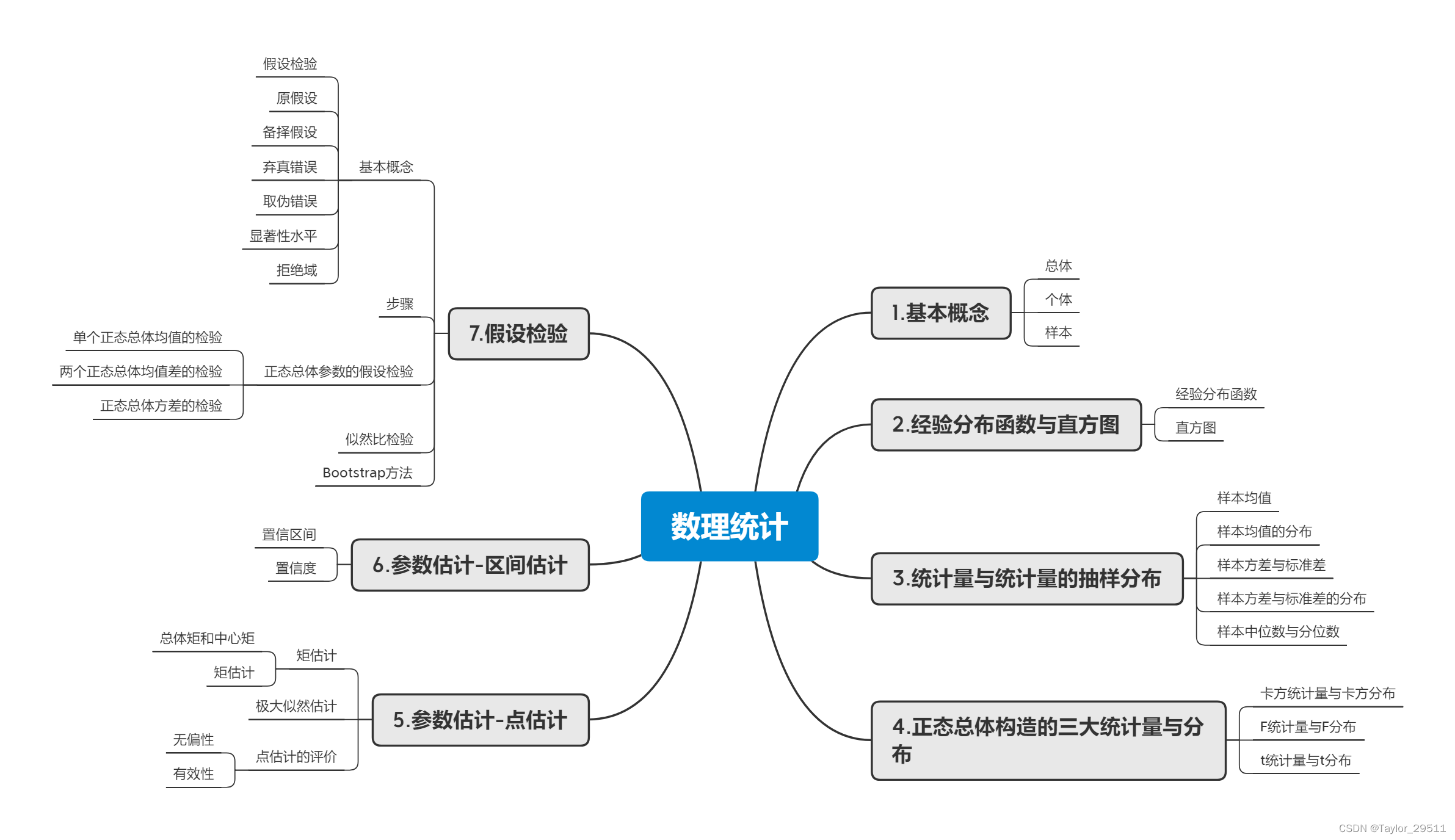


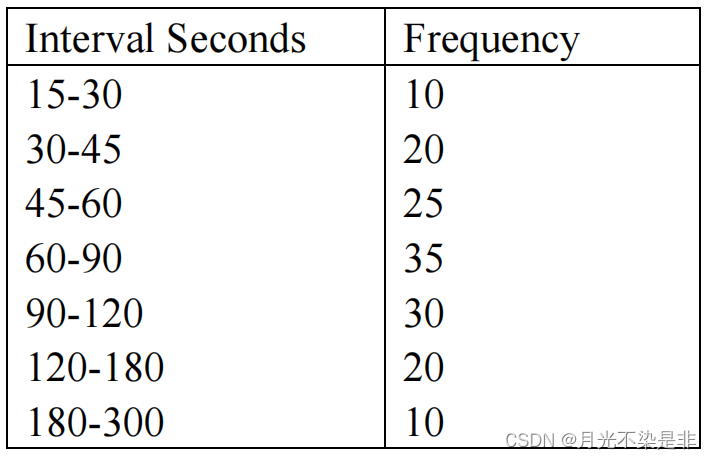
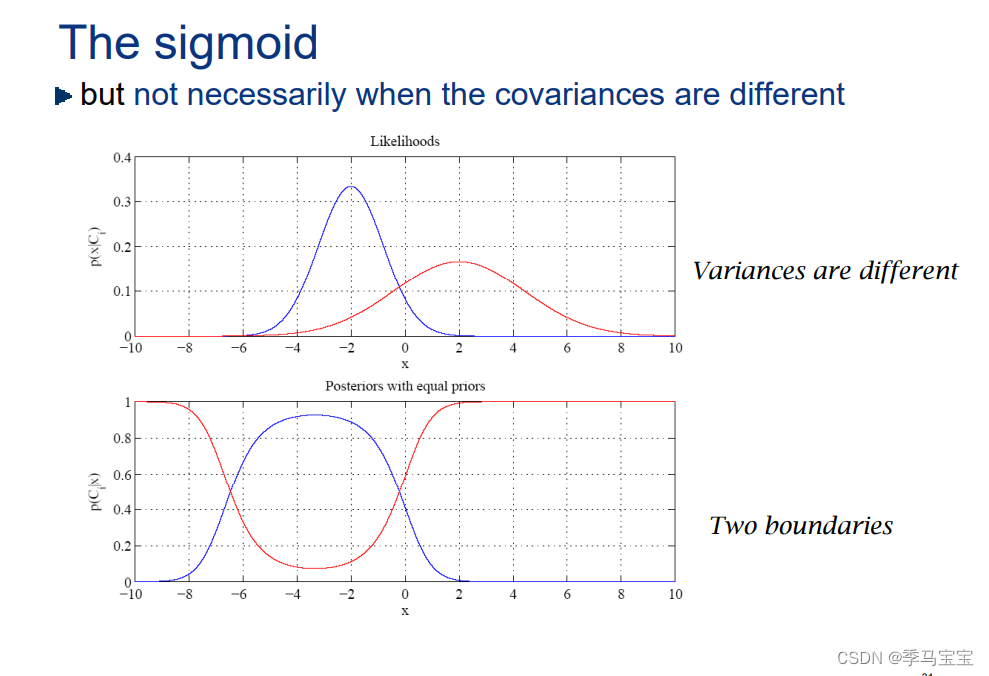


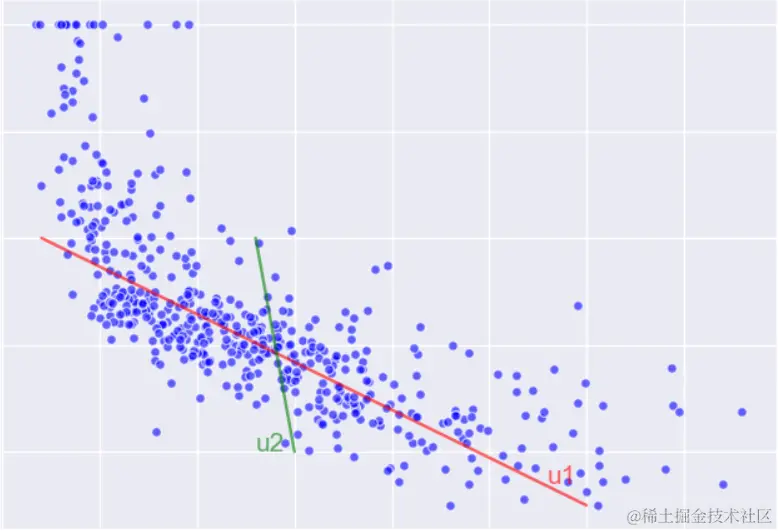
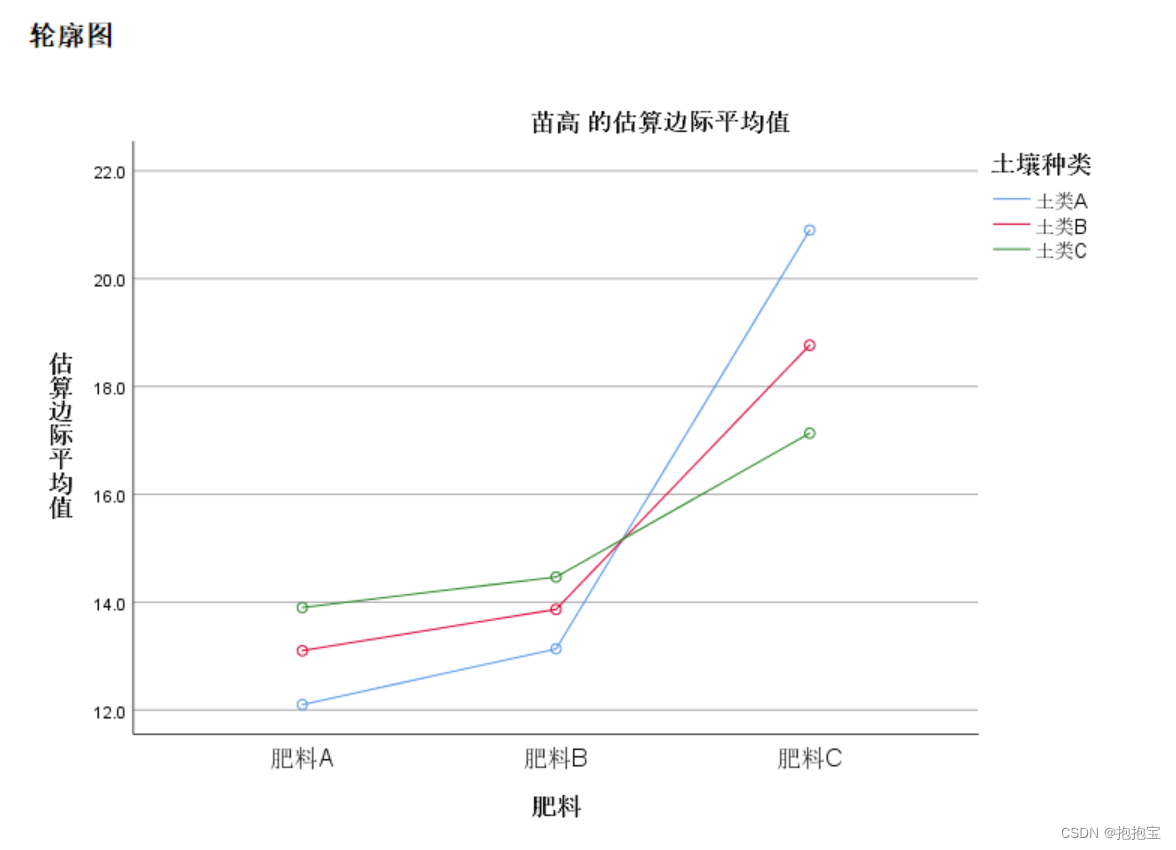

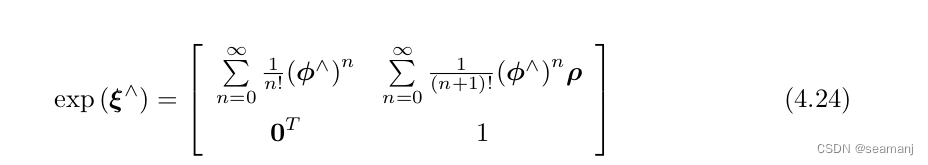
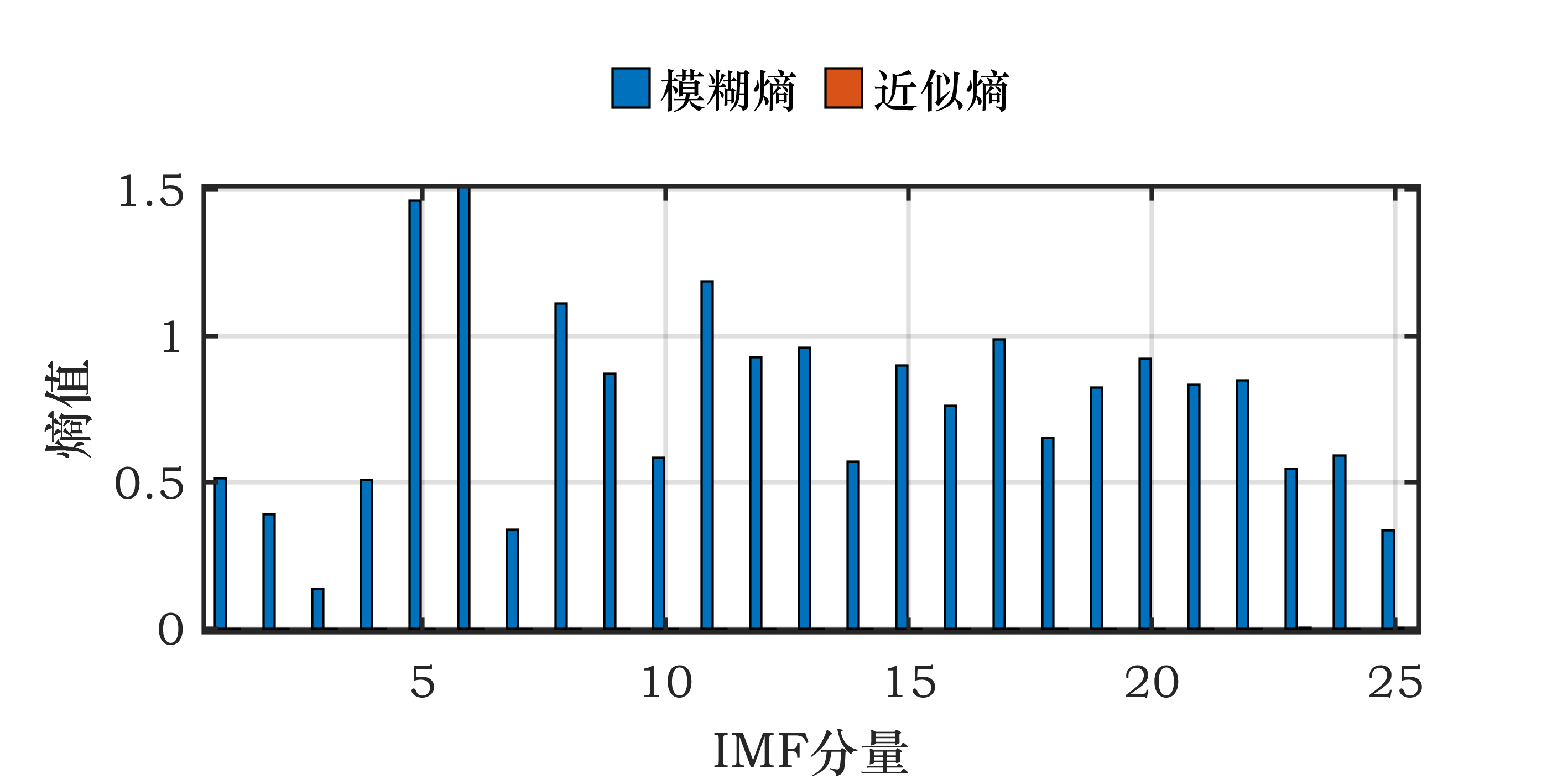

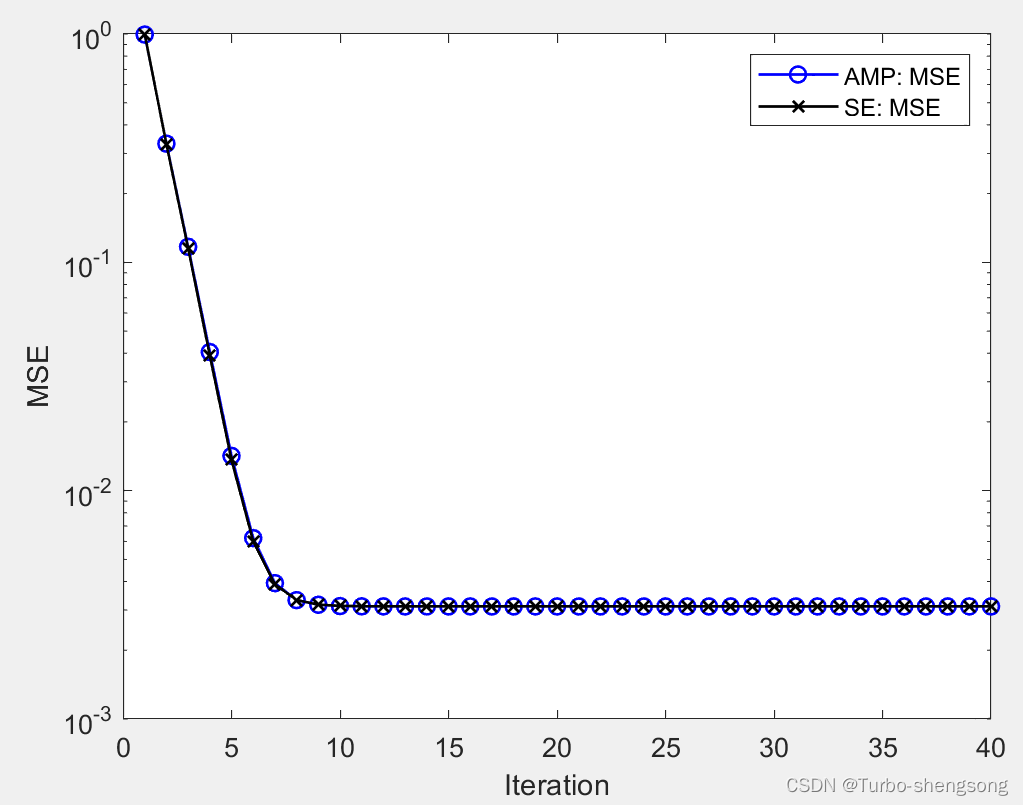
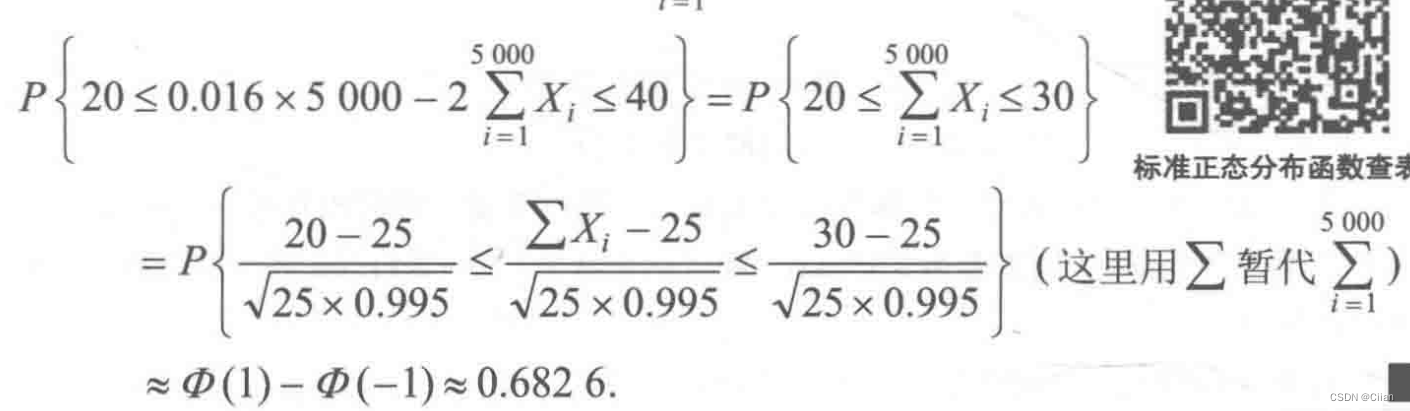

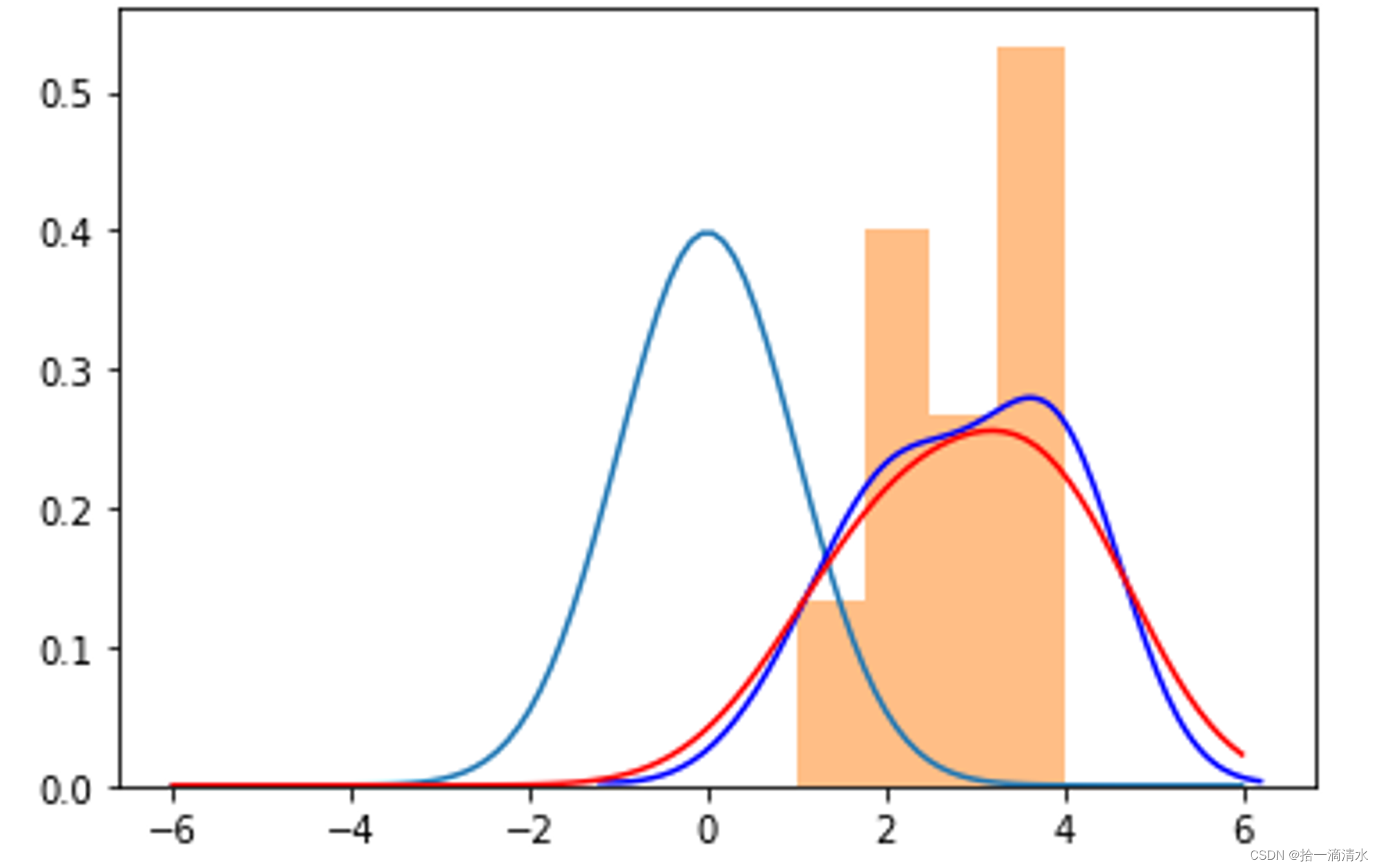
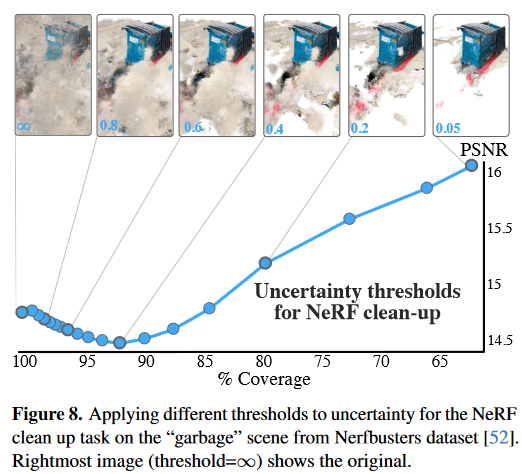


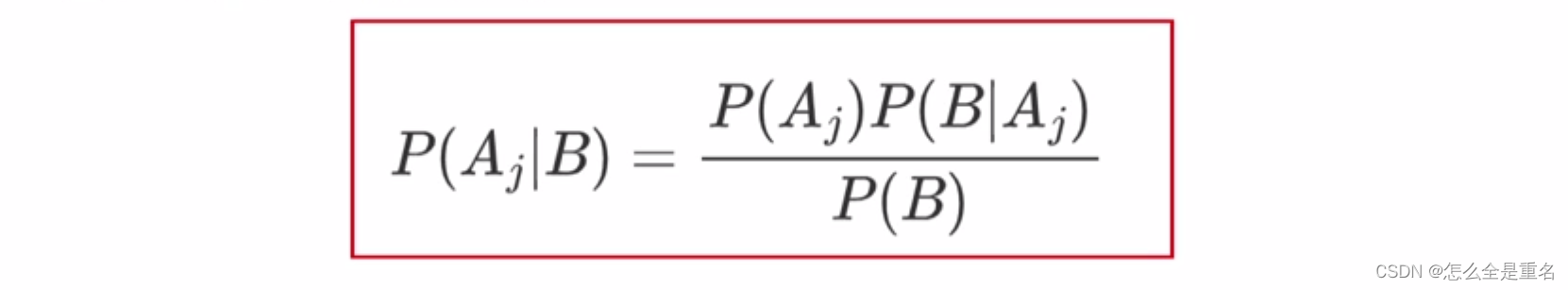
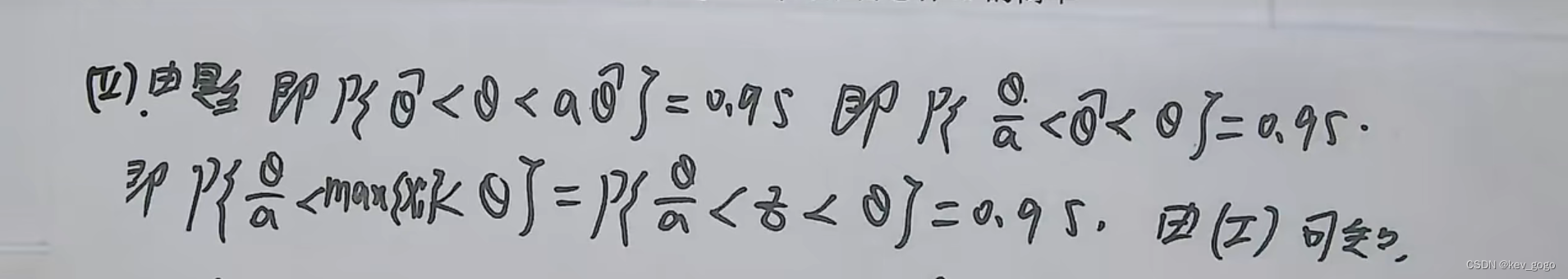

![50 个具有挑战性的概率问题 [第 5 部分]:方形硬币](https://img-blog.csdnimg.cn/img_convert/a3362f79316780d3250693a1cf956fc2.png)

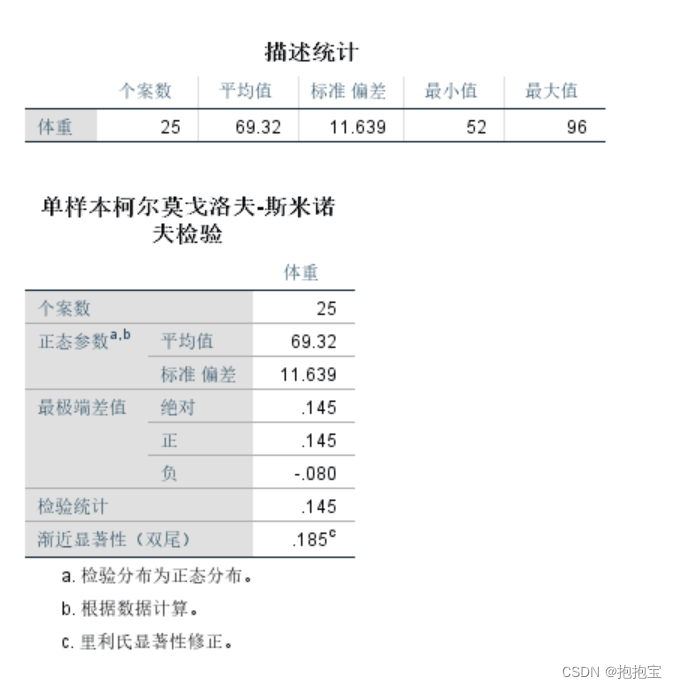



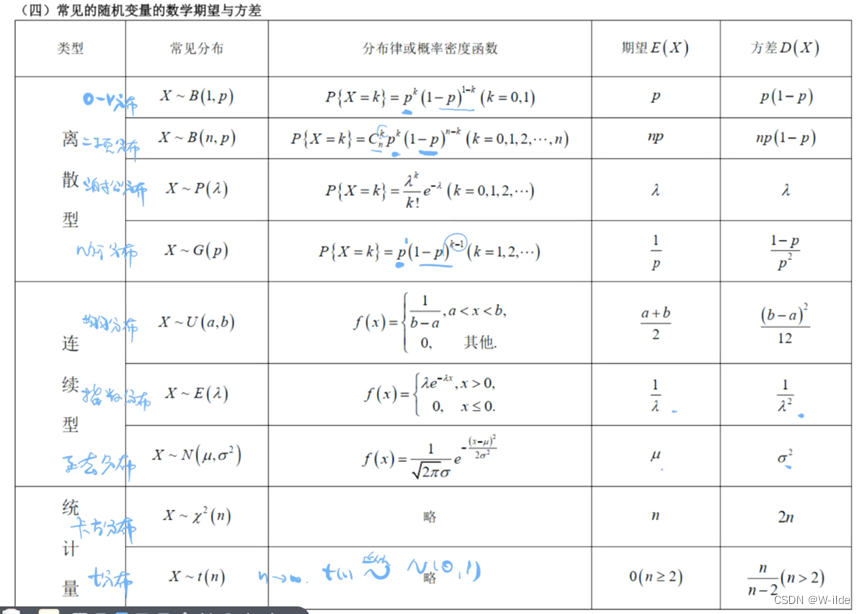
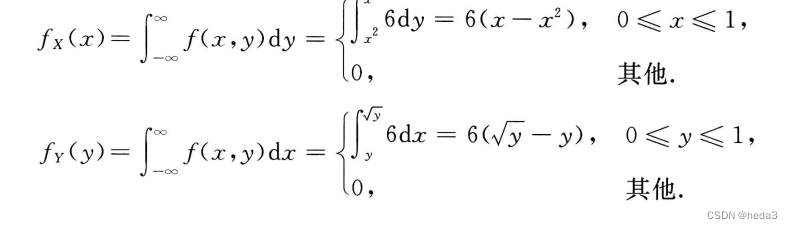
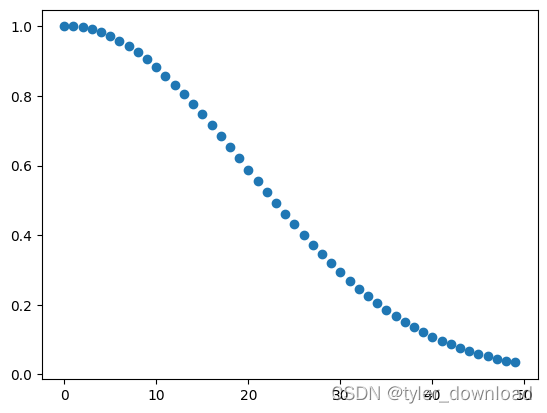

![概率论中的 50 个具有挑战性的问题 [第 6 部分]:Chuck-a-Luck](https://img-blog.csdnimg.cn/img_convert/d6fa4816e34e25896283d572da499b13.png)



![[概率论]四小时不挂猴博士](https://img-blog.csdnimg.cn/direct/7e6584ae35264f999035dc71194491e7.png)